Python ：自作関数のインポート（Brent法利用を含む）

はじめに

仕事で行う計算はJupyter notebookを利用して行っています．
よく使う150行ほどのプログラムを，そこら中にコピーを作って少しづつ書き換えながら使っていたのですが，どうもスマートでない．
そこで前半100行ほどの共通部分を自作関数としてモジュール化して使ってみることにしました．

そのプログラムそのものはかなりマニアックでみなさんに紹介してもスペースが無駄なので，これも少しマニアックですが，私が比較的よく使う簡単な計算プログラムをモジュール化した事例を紹介したいと思います．ここで紹介するプログラムも（プログラマではなく）設計技術者としての活用を少しだけ散りばめてみました．どこかのサンプルのコピーでは自分としての利用価値も小さくなってしまうので．
この記事に掲載したプログラムではモジュール化した数値計算部分が短いのでたいした省スペースにはなりませんが，この部分が長くなるとJupyter notebook の見た目もかなりスッキリしてきます．

モジュールの呼び出し方法は，以下の記事を参考にさせていただきました．
Pythonで簡単に自作関数を使いまわす

当方の環境は以下のとおりです．

• MacBook Pro (Retina, 13-inch, Mid 2014)
• macOS High Sierra
• Python 3.7.0

サンプルプログラム

モジュール化する前のプログラムを以下に示します．
このプログラムは，与えられた設計流量に対し，堰を超える流れの公式により流量を算出し，グラフ化するものです．
Brent法に利用にあたっては，このサンプルでは，求める値以外の引数を使っていること，求める値はよくサンプルにある x ではなく h としていることに注意してください．水深と言ったら x じゃなくて h じゃないの？程度のノリです．流量の値はゼロからでも，挟み込む初期値 h1=0 を指定できるので問題ないのですが，numpy.insert でnumpy配列の先頭にゼロを加える操作をしてみたかったので，流量はあえて 10 をスタートにしています．

# Water depth calculation
import numpy as np
import matplotlib.pyplot as plt
from scipy import optimize


def func1(h,q,b,w):
    # 解くべき方程式．イコールゼロの形で表現
    # 求めたい値は h．第一引数に指定
    # 流量係数 c は水深 h の関数であるため非線形方程式として処理
    c=1.28+1.42*h/w
    return q-c*b*h**(1.5)


def func2(h,b,w):
    # 検算用．水深 h を与えて流量 q を計算
    c=1.28+1.42*h/w
    q=c*b*h**(1.5)
    return q
    

def calc(b,w,q,h1,h2):
    # Brent法で解く．
    # func1：解くべき非線形方程式
    # h1, h2 ：解が存在するであろう範囲を指定する初期値
    # args ：func1 に渡す求めるべき値 (h) 以外の引数．
    hh=optimize.brentq(func1,h1,h2,args=(q,b,w))
    return hh


def drawfig(qd,hd):
    # グラフ化
    fsz=12
    plt.rcParams["font.size"] = fsz
    plt.rcParams['font.family'] ='sans-serif'
    fig=plt.figure(figsize=(6,4),facecolor='w')
    plt.xlabel('Discharge Q (m$^3$/s)')
    plt.ylabel('Water depth h (m)')
    plt.grid(color='#777777',linestyle='dashed')
    plt.plot(qd,hd,'-o')
    plt.show()


def main():
    # 制御部
    b=10.0   # 堰幅
    w=1.0    # 堰高
    h1=0.001 # Brent法のための初期値（小さい方の値）．zeroでもok
    h2=10    # Brent法のための初期値（大きい方の値）
    qd=np.arange(10,200,10) # 設計流量．zeroからでもok
    hd=np.zeros(len(qd),dtype=np.float64) # 水深を格納する配列の宣言
    for i,q in enumerate(qd): # 配列のインデックス指定のためenumerateでループのインデックスを取得
        hh=calc(b,w,q,h1,h2)  # 流量 q を与えBrent法で水深 hh を求める
        qq=func2(hh,b,w)      # 検算（水深 hh を与えて流量 qq を算出）
        print('{0:10.3f}{1:10.3f}{2:10.3f}'.format(hh,qq,qd[i]-qq)) # 結果表示
        hd[i]=hh              # 求めた水深 hh を配列に格納
    qd=np.insert(qd,0,0) # グラフ化用に配列の先頭にゼロ流量を追加
    hd=np.insert(hd,0,0) # グラフ化用に配列の先頭にゼロ水深を追加
    drawfig(qd,hd)       # グラフ作成
    
    
#==============
# Execution
#==============
if __name__ == '__main__': main()

関数のモジュール化とその利用

サンプルプログラムは以下の構成になっています．

• 数値計算部
• グラフ化部
• 条件入力および制御部

ここでどこをモジュールとして共通利用するかですが，

• 数値計算部は共通利用可能．公式は不変．主要パラメータは引数で制御可能
• グラフ化部は，堰の幅や高さを変えて複数の曲線を描画・比較したいなどのニーズがある
• 条件入力は個別に行う必要がある

ということを考え，数値計算部を共通利用部としてモジュール化することにします．

モジュール側

モジュール部は以下のとおりとし，名前を im_weir.py として '/Volumes/Transcend/pypro' というディレクトリに保存します．

im_weir.py

# im_weir.py
from scipy import optimize


def func1(h,q,b,w):
    c=1.28+1.42*h/w
    return q-c*b*h**(1.5)


def func2(h,b,w):
    c=1.28+1.42*h/w
    q=c*b*h**(1.5)
    return q


def calc(b,w,q,h1,h2):
    hh=optimize.brentq(func1,h1,h2,args=(q,b,w))
    return hh

呼び出し側

呼び出し側では，以下のようにモジュールのはいったディレクトリをPythonのパスに加えてからプログラムをインポートします．

import sys; sys.path.append('/Volumes/Transcend/pypro')
import im_weir

使い方は以下のようにします．

hh=im_weir.calc(b,w,q,h1,h2)
qq=im_weir.func2(hh,b,w)

呼び出し側プログラム全文

# Water depth calculation
import numpy as np
import matplotlib.pyplot as plt
import sys; sys.path.append('/Volumes/Transcend/pypro')
import im_weir


def drawfig(qd,hd):
    fsz=12
    plt.rcParams["font.size"] = fsz
    plt.rcParams['font.family'] ='sans-serif'
    fig=plt.figure(figsize=(6,4),facecolor='w')
    plt.xlabel('Discharge Q (m$^3$/s)')
    plt.ylabel('Water depth h (m)')
    plt.grid(color='#777777',linestyle='dashed')
    plt.plot(qd,hd,'-o')
    plt.show()


def main():
    b=10.0
    w=1.0
    h1=0.001 # zeroでもok
    h2=10
    qd=np.arange(10,200,10) # zeroからでもok
    hd=np.zeros(len(qd),dtype=np.float64)
    for i,q in enumerate(qd):
        hh=im_weir.calc(b,w,q,h1,h2)
        qq=im_weir.func2(hh,b,w)
        print('{0:10.3f}{1:10.3f}{2:10.3f}'.format(hh,qq,qd[i]-qq))
        hd[i]=hh
    qd=np.insert(qd,0,0)
    hd=np.insert(hd,0,0)
    drawfig(qd,hd)
    
    
#==============
# Execution
#==============
if __name__ == '__main__': main()

入力条件とグラフを変えてみる

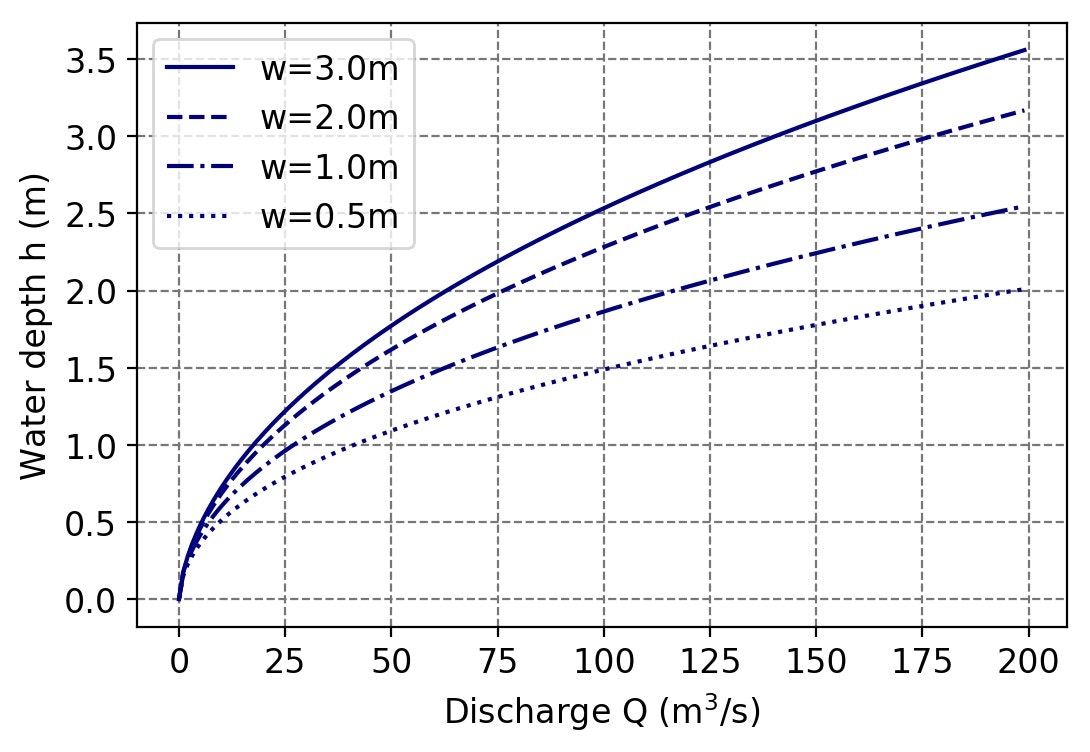
入力条件を変更（堰高４種類）とそれに対応してグラフを書き換えた事例です．
こんなグラフを描画・保存するプログラムです．やはり入力条件を変えるとグラフも書き換えざるを得ない場合が多く，モジュール化するには相当汎用性を持たせないと難しい感じです．またあまり汎用性をもたせようとするとやたらにパラメータが多くなり逆に使いづらくなりそう．この程度のグラフならコードのコピーと改良ですますのがトータル的に手がかからないように思います．なお，水深を格納する配列（２次元配列）の最初にゼロを加える操作は， hd=np.insert(hd,0,0,axis=0) により行っています．

書き換えた呼び出し側プログラム全文

# Water depth calculation
import numpy as np
import matplotlib.pyplot as plt
import sys; sys.path.append('/Volumes/Transcend/pypro')
import im_weir


def drawfig(qd,hd):
    fsz=12
    plt.rcParams["font.size"] = fsz
    plt.rcParams['font.family'] ='sans-serif'
    fig=plt.figure(figsize=(6,4),facecolor='w')
    plt.xlabel('Discharge Q (m$^3$/s)')
    plt.ylabel('Water depth h (m)')
    plt.grid(color='#777777',linestyle='dashed')
    plt.plot(qd,hd[:,3],'-' ,color='#000080',lw=1.5,label='w=3.0m')
    plt.plot(qd,hd[:,2],'--',color='#000080',lw=1.5,label='w=2.0m')
    plt.plot(qd,hd[:,1],'-.',color='#000080',lw=1.5,label='w=1.0m')
    plt.plot(qd,hd[:,0],':',color='#000080',lw=1.5,label='w=0.5m')
    plt.legend()
    fnameF='fig_weir.jpg'
    plt.savefig(fnameF, dpi=200, bbox_inches="tight", pad_inches=0.1)
    plt.show()


def main():
    b=10.0
    wh=np.array([0.5, 1.0, 2.0, 3.0]) # 堰高を4種類指定する
    h1=0.001 # zeroでもok
    h2=20
    qd=np.arange(1,200,1) # zeroからでもok
    hd=np.zeros((len(qd),len(wh)),dtype=np.float64)
    for n,w in enumerate(wh):     # 堰高のループ
        for i,q in enumerate(qd): # 流量のループ
            hh=im_weir.calc(b,w,q,h1,h2)
            qq=im_weir.func2(hh,b,w)
#            print('{0:10.3f}{1:10.3f}{2:10.3f}'.format(hh,qq,qd[i]-qq))
            hd[i,n]=hh
    qd=np.insert(qd,0,0)
    hd=np.insert(hd,0,0,axis=0)
    drawfig(qd,hd)
    
    
#==============
# Execution
#==============
if __name__ == '__main__': main()

以　上