はじめに
機械学習というのがはやっているようだが、私の仕事上では今のところ特に必要性はない。とは言いながら10連休中に何か新しいことをやってみようと思い、scikit-learnをいじってみようと思い立った。TensorFlowも触ってみたいのだが、いまだにPython3.7へのインストールはうまくいかないようなので、Python3.7に問題なくインストールできるscikit-learnにしたわけである。
手始めに行ってみたのが、重回帰分析。まずはnumpyを用いて自作し、同じ処理をscikit-learnで行ってみた。使用したサンプルデータは、scikit-learnに付属のボストン土地価格である。
参考にしたサイトは以下の通り。
scikit-learnのデータセット
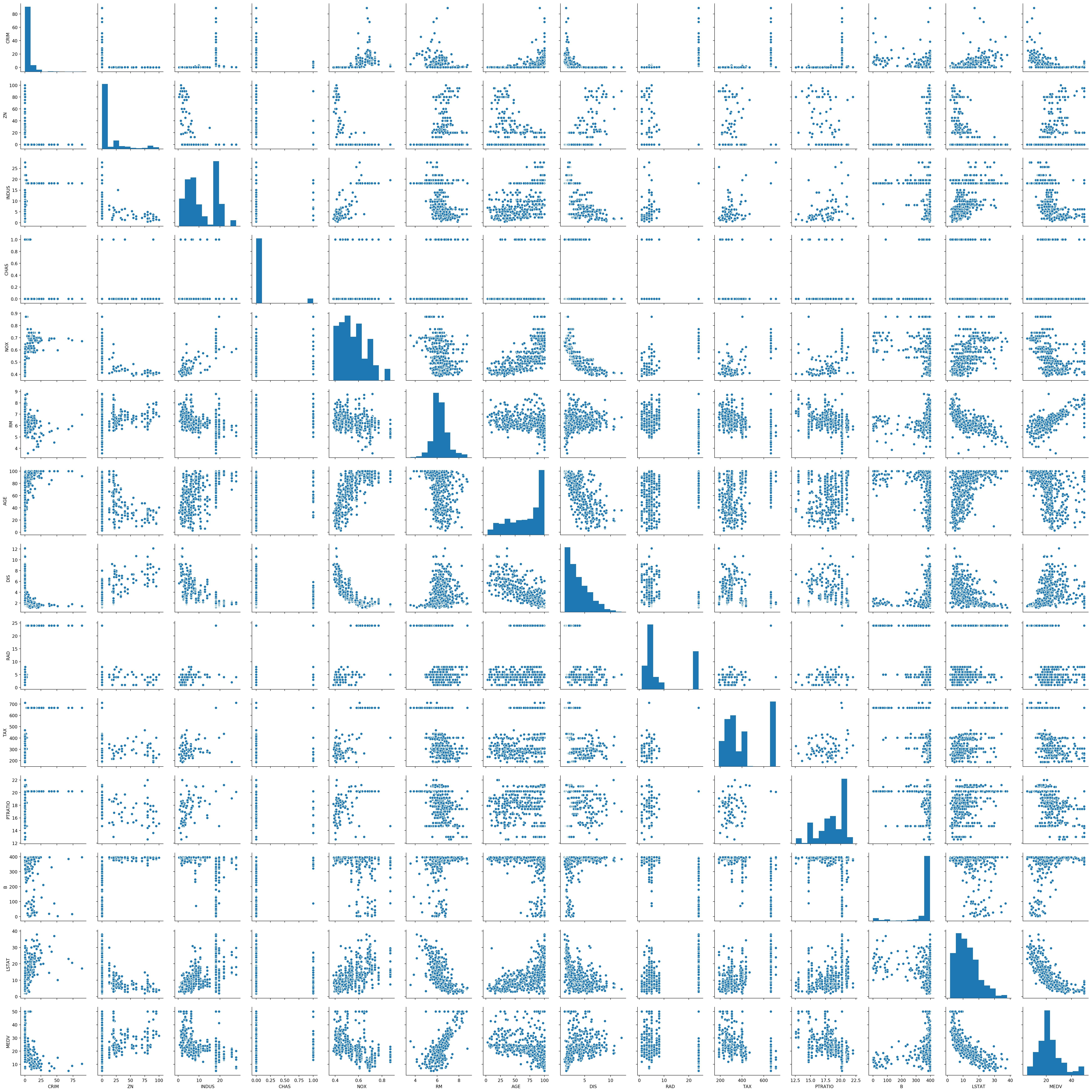
Pairplot
https://note.nkmk.me/python-seaborn-pandas-pairplot/
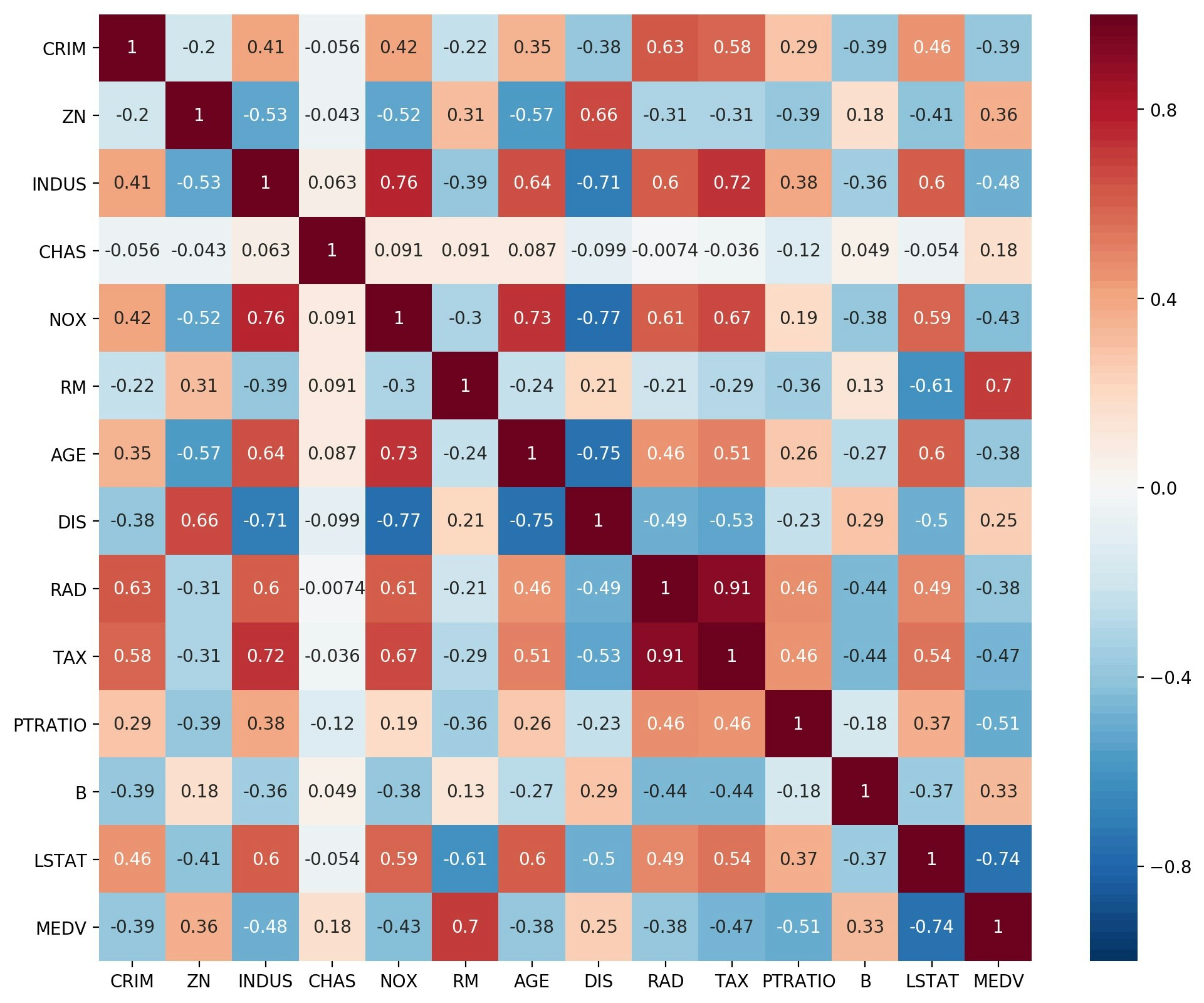
相関係数のheatmap
https://note.nkmk.me/python-pandas-corr/
今回紹介する内容は以下の通り。
前処理
サンプルデータとしてscikit-learn付属のデータベースを利用するため、以下の前処理を実行。
- データセットの解説を表示し目的変数名を確認
- データセットの内容を、メインプログラムで読み込むため、一度csvファイルとして保存。
- seabor のPairplotと相関行列のHeatmapでデータの関連線をざっくりと把握。
重回帰分析
重回帰分析プログラム本体での処理内容は以下の通り。今回の紹介事例では、オリジナルデータのままの回帰と、オリジナルデータを標準化(平均値:0、標準偏差:1)したものの回帰を行っている。
- csvファイルよりデータ読み込み
- 正規方程式を作成し、
np.linalg.solveで解く - 目的変数と回帰推定値の重相関係数を算出
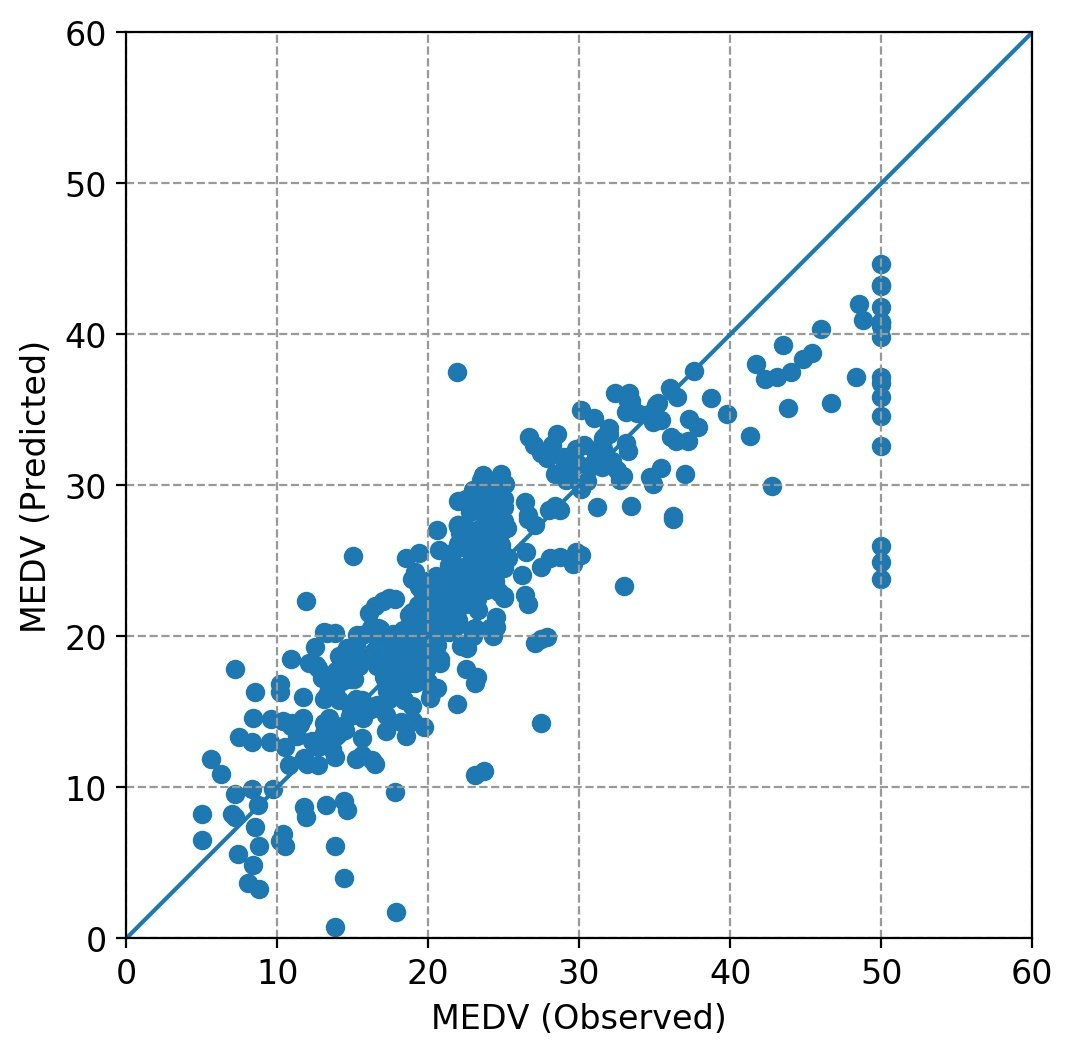
- 目的変数(観測値)と回帰推定値の関係をプロット
ここでは練習なので、説明変数の吟味・選択は行わず、全変数を使った計算をしている。
データセットの解説を見る
import pandas as pd
from sklearn import datasets
dataset = datasets.load_boston()
print(dataset.DESCR)
これにより、MEDV という変数が目的変数(下記説明では target)であることがわかる。
.. _boston_dataset:
Boston house prices dataset
---------------------------
**Data Set Characteristics:**
:Number of Instances: 506
:Number of Attributes: 13 numeric/categorical predictive. Median Value (attribute 14) is usually the target.
:Attribute Information (in order):
- CRIM per capita crime rate by town
- ZN proportion of residential land zoned for lots over 25,000 sq.ft.
- INDUS proportion of non-retail business acres per town
- CHAS Charles River dummy variable (= 1 if tract bounds river; 0 otherwise)
- NOX nitric oxides concentration (parts per 10 million)
- RM average number of rooms per dwelling
- AGE proportion of owner-occupied units built prior to 1940
- DIS weighted distances to five Boston employment centres
- RAD index of accessibility to radial highways
- TAX full-value property-tax rate per $10,000
- PTRATIO pupil-teacher ratio by town
- B 1000(Bk - 0.63)^2 where Bk is the proportion of blacks by town
- LSTAT % lower status of the population
- MEDV Median value of owner-occupied homes in $1000's
:Missing Attribute Values: None
:Creator: Harrison, D. and Rubinfeld, D.L.
This is a copy of UCI ML housing dataset.
https://archive.ics.uci.edu/ml/machine-learning-databases/housing/
This dataset was taken from the StatLib library which is maintained at Carnegie Mellon University.
The Boston house-price data of Harrison, D. and Rubinfeld, D.L. 'Hedonic
prices and the demand for clean air', J. Environ. Economics & Management,
vol.5, 81-102, 1978. Used in Belsley, Kuh & Welsch, 'Regression diagnostics
...', Wiley, 1980. N.B. Various transformations are used in the table on
pages 244-261 of the latter.
The Boston house-price data has been used in many machine learning papers that address regression
problems.
.. topic:: References
- Belsley, Kuh & Welsch, 'Regression diagnostics: Identifying Influential Data and Sources of Collinearity', Wiley, 1980. 244-261.
- Quinlan,R. (1993). Combining Instance-Based and Model-Based Learning. In Proceedings on the Tenth International Conference of Machine Learning, 236-243, University of Massachusetts, Amherst. Morgan Kaufmann.
データのファイル化
一般的なデータ処理を考え、scikit-learn付属のデータセットをcsvファイルに書き込み保存する。
import pandas as pd
from sklearn import datasets
dataset = datasets.load_boston()
df = pd.DataFrame(dataset.data,columns=dataset.feature_names)
df['MEDV'] = dataset.target
pd.options.display.float_format = '{:10.4f}'.format
print(df.head())
df.to_csv('boston.csv', index=False)
作成したデータフレームの表示結果(先頭付近)は以下の通り。
CRIM ZN INDUS CHAS NOX RM \
0 0.0063 18.0000 2.3100 0.0000 0.5380 6.5750
1 0.0273 0.0000 7.0700 0.0000 0.4690 6.4210
2 0.0273 0.0000 7.0700 0.0000 0.4690 7.1850
3 0.0324 0.0000 2.1800 0.0000 0.4580 6.9980
4 0.0691 0.0000 2.1800 0.0000 0.4580 7.1470
AGE DIS RAD TAX PTRATIO B \
0 65.2000 4.0900 1.0000 296.0000 15.3000 396.9000
1 78.9000 4.9671 2.0000 242.0000 17.8000 396.9000
2 61.1000 4.9671 2.0000 242.0000 17.8000 392.8300
3 45.8000 6.0622 3.0000 222.0000 18.7000 394.6300
4 54.2000 6.0622 3.0000 222.0000 18.7000 396.9000
LSTAT MEDV
0 4.9800 24.0000
1 9.1400 21.6000
2 4.0300 34.7000
3 2.9400 33.4000
4 5.3300 36.2000
ざっくりとデータを眺める
ざっくりとデータを眺めるため、seaborn の pairplot と、相関行列の heatmap を描いてみた。
これらにより、目的変数の説明に必要な変数が、直感的にわかる。
seaborn を使うのは初めてだが、簡単な操作で作図が実現でき、とても便利。
Heatmap の色は、相関係数の表示なので、最小0、最大1、中央0としているところがミソです。でもなんとなくパッとしない感じなので、もっといい感じにしたい。
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
fnameR='boston.csv' # input file name
df = pd.read_csv(fnameR, sep=',') # data input as a DataFrame
sns.pairplot(df)
fnameF='fig_mra1.jpg'
plt.savefig(fnameF, dpi=200, bbox_inches="tight", pad_inches=0.1)
plt.show()
cm=np.corrcoef(df.transpose())
plt.figure(figsize=(12, 10))
cmap = sns.color_palette("RdBu_r", 100)
sns.heatmap(cm, annot=True,vmax=1,vmin=-1,center=0,cmap=cmap,xticklabels=df.columns,yticklabels=df.columns)
fnameF='fig_mra2.jpg'
plt.savefig(fnameF, dpi=200, bbox_inches="tight", pad_inches=0.1)
plt.show()
Pairplot
相関行列のHeatmap
numpyを用いた自作
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
def drawfig(yd,ye,ystr):
fsz=12
xmin=0;xmax=60
ymin=0;ymax=60
plt.figure(figsize=(6,6),facecolor='w')
plt.rcParams['font.size']=fsz
plt.rcParams['font.family']='sans-serif'
plt.xlim([xmin,xmax])
plt.ylim([ymin,ymax])
plt.xlabel(ystr+' (Observed)')
plt.ylabel(ystr+' (Predicted)')
plt.grid(color='#999999',linestyle='dashed')
plt.gca().set_aspect('equal',adjustable='box')
plt.scatter(yd,ye)
plt.plot([xmin,xmax],[ymin,ymax],'-')
fnameF='fig_mra.jpg'
plt.savefig(fnameF, dpi=200, bbox_inches="tight", pad_inches=0.1)
plt.show()
def calc(df,ystr):
x1=df.drop(ystr, axis=1).values # create numpy array of data without objective variable
x2=np.ones((len(df),1),dtype=np.float64) # create column vector with values of one
xd=np.hstack([x1,x2]) # create data matrix with conjunction of numpy arrays
yd=df[ystr].values # create column vector of objective variable
aa=np.dot(xd.T,xd) # normal equation (1)
bb=np.dot(yd,xd) # normal equation (2)
cc=np.linalg.solve(aa,bb) # splve normal equation
ye=np.dot(xd,cc) # estimate predicted values
rr=np.corrcoef(yd,ye)[0][1] # multiple correlation coefficient
coef=np.append(cc,rr) # partial regression coefficients + r
return yd,ye,coef
def main():
fnameR='boston.csv' # input file name
ystr='MEDV' # name of objective variable
df = pd.read_csv(fnameR, sep=',') # data input as a DataFrame
cname=[]
cname.extend(df.columns.values) # add column names in the list
cname.remove(ystr) # remove objective variable name from list
cname.extend(['constant','r']) # add names of 'constant' and 'r' in the list
yd1,ye1,coef1=calc(df,ystr) # calculation for multiple regression analysis
drawfig(yd1,ye1,ystr) # draw a relationship between observed data and predicted data
y_mean=np.mean(df,axis=0) # mean of each column
y_std=np.std(df,axis=0,ddof=1) # standard deviation of each column by N-doff
df=(df-y_mean)/y_std # standardization
yd2,ye2,coef2=calc(df,ystr) # calculation for multiple regression analysis
pd.options.display.float_format = '{:15.4f}'.format
dfr=pd.DataFrame({'Name':cname,'Original':coef1,'STD':coef2})
print(dfr.to_string(index=False))
if __name__ == '__main__':
main()
scikit-learnを用いた実装
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn import linear_model
def drawfig(yd,ye,ystr):
fsz=12
xmin=0;xmax=60
ymin=0;ymax=60
plt.figure(figsize=(6,6),facecolor='w')
plt.rcParams['font.size']=fsz
plt.rcParams['font.family']='sans-serif'
plt.xlim([xmin,xmax])
plt.ylim([ymin,ymax])
plt.xlabel(ystr+' (Observed)')
plt.ylabel(ystr+' (Predicted)')
plt.grid(color='#999999',linestyle='dashed')
plt.gca().set_aspect('equal',adjustable='box')
plt.scatter(yd,ye)
plt.plot([xmin,xmax],[ymin,ymax],'-')
plt.show()
def calc(df,ystr):
clf = linear_model.LinearRegression()
xd = df.drop(ystr, axis=1).values # create data matrix without objective variable
yd = df[ystr].values # create column vector of objective variable
clf.fit(xd,yd)
ye = clf.predict(xd) # estimate predicted values
const=clf.intercept_ # constant term
rr=np.sqrt(clf.score(xd, yd)) # multiple correlation coefficient
coef=np.append(clf.coef_,const) # conjunction of partial regression coefficients and constant term
coef=np.append(coef,rr) # append correlation coefficient to regression coefficient vector
return yd,ye,coef
def main():
fnameR='boston.csv' # input file name
ystr='MEDV' # name of objective variable
df = pd.read_csv(fnameR, sep=',') # data unput
cname=[]
cname.extend(df.columns.values) # add column names in the list
cname.remove(ystr) # remove objective variable name from list
cname.extend(['constant','r']) # add names of 'constant' and 'r' in the list
yd1,ye1,coef1=calc(df,ystr) # calculation for multiple regression analysis
drawfig(yd1,ye1,ystr) # draw a relationship between observed data and predicted data
y_mean=np.mean(df,axis=0) # mean of each column
y_std=np.std(df,axis=0,ddof=1) # standard deviation of each column by N-doff
df=(df-y_mean)/y_std # standardization
yd2,ye2,coef2=calc(df,ystr)
pd.options.display.float_format = '{:15.4f}'.format
dfr=pd.DataFrame({'Name':cname,'Original':coef1,'STD':coef2})
print(dfr.to_string(index=False))
if __name__ == '__main__':
main()
出力事例
下記は画面出力事例。
Nameは変数名、Originalは生データのまま、STDは生データを標準化処理(平均値:0、標準偏差:1)したものの処理結果。
Name Original STD
CRIM -0.1080 -0.1010
ZN 0.0464 0.1177
INDUS 0.0206 0.0153
CHAS 2.6867 0.0742
NOX -17.7666 -0.2238
RM 3.8099 0.2911
AGE 0.0007 0.0021
DIS -1.4756 -0.3378
RAD 0.3060 0.2897
TAX -0.0123 -0.2260
PTRATIO -0.9527 -0.2243
B 0.0093 0.0924
LSTAT -0.5248 -0.4074
constant 36.4595 -0.0000
r 0.8606 0.8606
感想
- データをざっくり見るため、seabornでPairplotと相関行列のHeatmapを作ってみたが、とても簡単にでき、便利である。
- 回帰分析だけのコーディング量は、自作でもscukit-learn利用でもそれほど変わらない。
- 画面出力、csv出力するなら、pandasのDetaFrameとして書き出すのが便利である。
- 最近の仕事で統計分析をすることはないのだが、勉強がてらいろいろやってみようと思う。
以 上