1.はじめに
最近,自作の3次元骨組構造解析プログラムで計算を行っているが,自由度が大きくなると計算に時間がかかるのが気になりだしました.
6000自由度(行列サイズは 6000 x 6000)となると,numpy.linalg.solve では計算時間は10秒近くかかります.これを何十ケースもやるとなると,コンピュータの前で待っているのは手持ち無沙汰です.そこで何か早くする方法はないものかと探っていて見つけた方法が,scipyの疎行列計算の活用です.
結果からいうと,下表の通り,疎行列処理の導入により,十分に早くなります.自由度が小さく1秒以下の計算での違いなどは気になりませんが,自由度が大きい場合に1ケース9秒が3秒になる時間短縮は大きい!そこで,この記事では,疎行列計算ライブラリを用いた連立一次方程式解法の簡単な例と,実際のFEMプログラムへの実装を説明します.実装と行っても,プログラムの冒頭でライブラリを読み込んで,少し行列を変形するだけですが...
| 自由度 (行列サイズ:n x n) | n = 864 | n = 2166 | n = 6012 | 備考 |
|---|---|---|---|---|
| numpy.linalg.solve | 0.125 sec | 0.677 sec | 8.909 sec | 疎行列処理なし |
| scipy.sparse.linalg.spsolve | 0.123 sec | 0.411 sec | 2.645 sec | 疎行列処理あり |
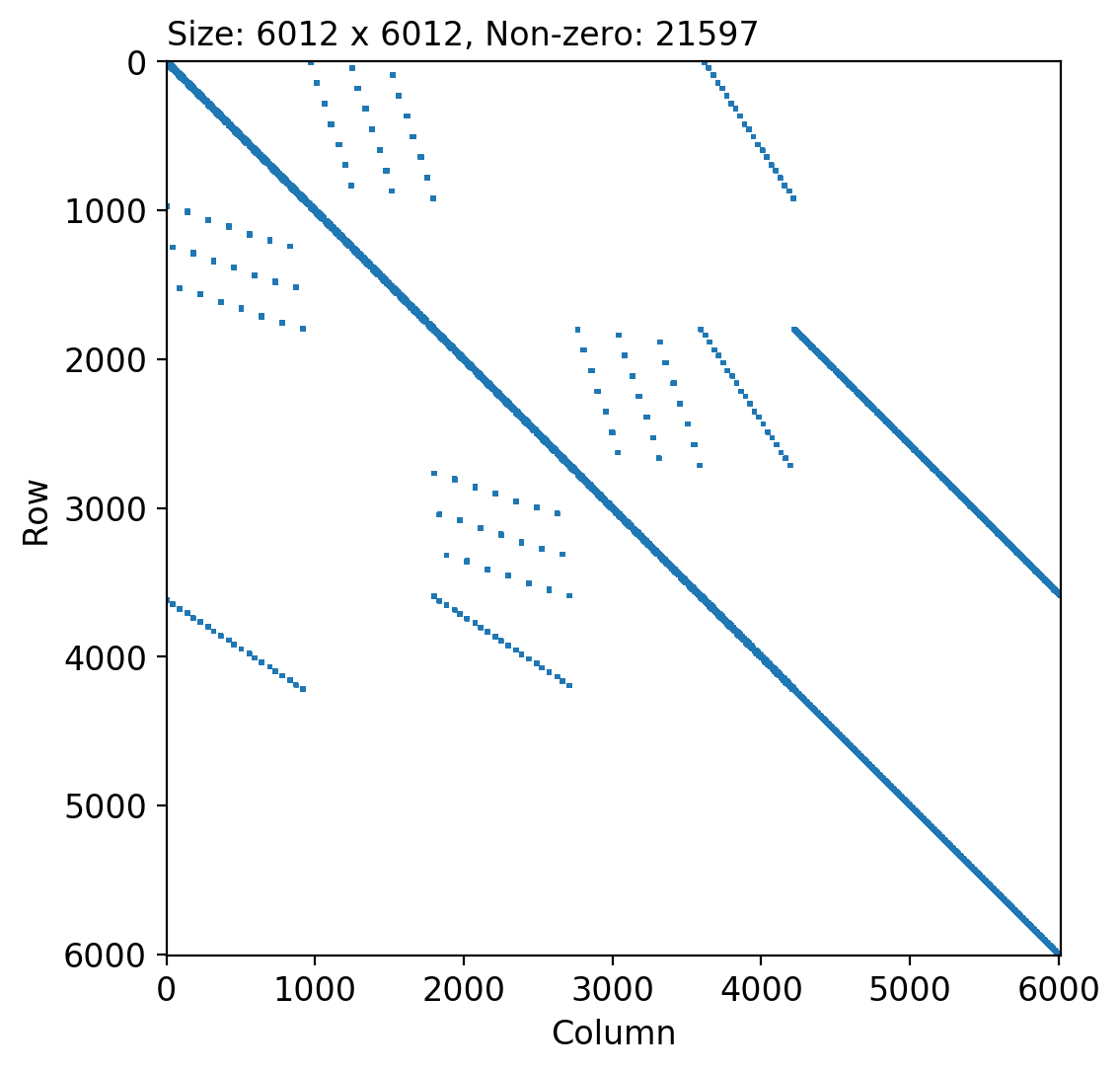
ちなみにどのくらい疎か,n=6012 の例で見てみると...たしかに疎だ.これを縦横全部チェックするのは非効率だし,バンド化しても空白域は大きい.疎行列処理のテクニックを導入するのがよかろうと思うわけです.なお,拘束節点処理後なのでもちろん対称ではありません.もし対称だったら大問題...特異行列で解けません.
(関連リンク)
2.Scipy 疎行列ライブラリの利用
以下のサイトを参考にしました.
- http://www.turbare.net/transl/scipy-lecture-notes/advanced/scipy_sparse/solvers.html#sparse-direct-solvers
- https://ohke.hateblo.jp/entry/2018/01/07/230000
- http://hamukazu.com/2014/09/26/scipy-sparse-basics/
- http://hamukazu.com/2014/12/03/internal-data-structure-scipy-sparse/
簡単な連立一次方程式を解いてみる(1)
上述サイトを参考に,以下のプログラムを作成して実行.
import numpy as np
from scipy.sparse.linalg import dsolve
aa=np.array([[ 1, 5, 0, 0, 0],
[ 0, 2, 8, 0, 0],
[ 0, 0, 3, 9, 0],
[ 0, 0, 0, 4, 10],
[ 0, 0, 0, 0, 5]],dtype=np.float64)
bb=np.array([1, 2, 3, 4, 5], dtype=np.float64)
x = dsolve.spsolve(aa, bb, use_umfpack=True)
print('x=',x)
print('Error=',np.dot(aa,x)-bb)
結果は以下の通り.解けていますが,警告が出ています.「spsplve に放り込むには,CSC か CSR マトリックスのフォーマットにしてね.」ということのようです.私は記法の違いを完全に理解していませんが,とりあえず「CSR」を採用(こちらが参考になります).
x= [106. -21. 5.5 -1.5 1. ]
Error= [0. 0. 0. 0. 0.]
/usr/local/lib/python3.7/site-packages/scipy/sparse/linalg/dsolve/linsolve.py:133: SparseEfficiencyWarning: spsolve requires A be CSC or CSR matrix format
SparseEfficiencyWarning)
簡単な連立一次方程式を解いてみる(2)
次に以下を実行.lil_matrix と csr 形式に書き換える tocsr() を使うため,
from scipy.sparse import lil_matrix, csr_matrix をインポート.
lil_matrix は,次元は元の行列と同じですが,非ゼロ項のみを記憶するものらしい.
import numpy as np
from scipy.sparse.linalg import dsolve
from scipy.sparse import lil_matrix, csr_matrix
aa=np.array([[ 1, 5, 0, 0, 0],
[ 0, 2, 8, 0, 0],
[ 0, 0, 3, 9, 0],
[ 0, 0, 0, 4, 10],
[ 0, 0, 0, 0, 5]],dtype=np.float64)
cc=aa
bb = np.array([1, 2, 3, 4, 5], dtype=np.float64)
aa=lil_matrix(aa).tocsr()
print(aa.shape)
print(aa)
x = dsolve.spsolve(aa, bb, use_umfpack=True)
print('x=',x)
print('Error=',np.dot(cc,x)-bb)
結果は以下の通り.警告なしで正解が出ている模様.
(5, 5)
(0, 0) 1.0
(0, 1) 5.0
(1, 1) 2.0
(1, 2) 8.0
(2, 2) 3.0
(2, 3) 9.0
(3, 3) 4.0
(3, 4) 10.0
(4, 4) 5.0
x= [106. -21. 5.5 -1.5 1. ]
Error= [-1.42108547e-14 0.00000000e+00 -3.55271368e-15 0.00000000e+00
0.00000000e+00]
簡単な連立一次方程式を問いてみる(3)
scipy のドキュメントを見ていたら,csr_matrix については,lil_matrix を介さなくてもそのまま変換できそうであること,
spsolve についても dsolve を介さなくても使えそうなことがわかったので,記述量を減らしました.
- scipy.sparse.csr_matrix https://docs.scipy.org/doc/scipy/reference/generated/scipy.sparse.csr_matrix.html#scipy.sparse.csr_matrix
- scipy.sparse.linalg.spsolve https://docs.scipy.org/doc/scipy/reference/generated/scipy.sparse.linalg.spsolve.html#scipy.sparse.linalg.spsolve
import numpy as np
from scipy.sparse.linalg import spsolve
from scipy.sparse import csr_matrix
aa=np.array([[ 1, 5, 0, 0, 0],
[ 0, 2, 8, 0, 0],
[ 0, 0, 3, 9, 0],
[ 0, 0, 0, 4, 10],
[ 0, 0, 0, 0, 5]],dtype=np.float64)
cc=aa
bb = np.array([1, 2, 3, 4, 5], dtype=np.float64)
aa=csr_matrix(aa)
print(aa.shape)
print(aa)
x = spsolve(aa, bb, use_umfpack=True)
print('x=',x)
print('Error=',np.dot(cc,x)-bb)
出力はもちろん(2)と同じです.
(5, 5)
(0, 0) 1.0
(0, 1) 5.0
(1, 1) 2.0
(1, 2) 8.0
(2, 2) 3.0
(2, 3) 9.0
(3, 3) 4.0
(3, 4) 10.0
(4, 4) 5.0
x= [106. -21. 5.5 -1.5 1. ]
Error= [-1.42108547e-14 0.00000000e+00 -3.55271368e-15 0.00000000e+00
0.00000000e+00]
結局どうするのか? 上述(3)をベースに.
(a)以下をインポート
import numpy as np
from scipy.sparse.linalg import spsolve
from scipy.sparse import csr_matrix
(b)連立一次方程式 $\{b\}=[A]\{x\}$ の行列 $aa=[A]$ とベクトル $bb=\{b\}$ を numpy 配列で作成.
(c)以下に示すように,行列 $aa$ を csr_matrix で変形し,ベクトル $bb$ とともに dsolve.spsolve に突っ込めば終わり.
aa=csr_matrix(aa)
x = spsolve(aa, bb, use_umfpack=True)
付録:どのくらい疎なのかを見てみる
CSR 形式の行列を保存するには,
numpy.save('array',gk) # arrayはファイル名
でOK (numpy.save) .array.npy というバイナリファイルが出来上がります.これを読み込んで非ゼロ要素を表示するプログラムは以下の通り.前出の図を描くプログラムです.CSR を toarray でフルの正方行列に戻し,for 文を2重にまわして非ゼロ要素を探しているので,遅いです.もっといい方法がありそうなのだけど,今の所思いつかない.
# np.save('array',gk): save an array to a binary file in Numpy .npy format.
# a .npy extension is appended to the file name.
import numpy as np
import matplotlib.pyplot as plt
gk=np.load('array.npy')
gk=gk.any().toarray()
n=gk.shape[0]
m=gk.shape[1]
x=[]
y=[]
for i in range(0,n):
for j in range(0,m):
if 0<abs(gk[i,j]):
x=x+[float(i)]
y=y+[float(j)]
fsz=12
xmin=0
xmax=float(m-1)
ymin=0
ymax=float(n-1)
fig=plt.figure(figsize=(6,6),facecolor='w')
plt.rcParams['font.size']=fsz
plt.rcParams['font.family']='sans-serif'
plt.xlim([xmin,xmax])
plt.ylim([ymax,ymin])
plt.xlabel('Column')
plt.ylabel('Row')
plt.gca().set_aspect('equal',adjustable='box')
plt.plot(x,y,'s',ms=1)
strt='Size: {0:d} x {1:d}, Non-zero: {2:d}'.format(n,m,len(x))
plt.title(strt,loc='left',fontsize=fsz)
fnameF='fig_sparse.png'
plt.savefig(fnameF, dpi=200, bbox_inches="tight", pad_inches=0.1)
plt.show()
3.実プログラム(3次元骨組構造解析プログラム)
こちらの記事で紹介した,3次元骨組構造解析プログラムを改造したものを紹介します.昔のプログラムからは,以下の点をいじっています.
- 疎行列処理導入による高速化
- 関数名を小文字にした
- データ入力部を関数にした
- 計算用関数(データ入力・プリントアウト部を除く)の引数を全てスカラーとした
- 無意味な配列初期化の部分をカットした
- 配列初期化時の形状をタプルで指定するようにした(何故かこれまでリストで渡していた)
- メインルーチンも関数化した.これは下の記事を見てハット思い実行しました.これによりグローバル変数となっているものを関数の引数で呼び込んだりというおかしなことがなくなったと思います.(pythonで小さなツールを作る時のtips)
この疎行列を扱う scipy ライブラリを使う方法は,2次元応力解析など,自由度が大きなモデルの連立一次方程式を解くのに有効に使えそうです.
疎行列導入に伴い変えるところ
splolve と csr_matrix のインポートを追加.
from scipy.sparse.linalg import spsolve
from scipy.sparse import csr_matrix
剛性マトリックスの境界条件処理後,全体剛性マトリックス gk を CSR フォーマットに書き換えて,spsolve に渡します.numpy の np.linalg.solve はコメントアウトしています.
# solution of simultaneous linear equations
# disg = np.linalg.solve(gk, fp)
gk = csr_matrix(gk)
disg = spsolve(gk, fp, use_umfpack=True)
プログラム全文
# ======================
# 3D Frame Analysis
# ======================
import numpy as np
from scipy.sparse.linalg import spsolve
from scipy.sparse import csr_matrix
import sys
import time
def inpdata_3dfrm(fnameR,nod,nfree):
f=open(fnameR,'r')
text=f.readline()
text=text.strip()
text=text.split()
npoin=int(text[0]) # Number of nodes
nele =int(text[1]) # Number of elements
nsec =int(text[2]) # Number of sections
npfix=int(text[3]) # Number of restricted nodes
nlod =int(text[4]) # Number of loaded nodes
# array declaration
ae =np.zeros((12,nsec),dtype=np.float64) # Section characteristics
node =np.zeros((nod+1,nele),dtype=np.int) # node-element relationship
x =np.zeros((3,npoin),dtype=np.float64) # Coordinates of nodes
deltaT=np.zeros(npoin,dtype=np.float64) # Temperature change of nodes
mpfix =np.zeros((nfree,npoin),dtype=np.int) # Ristrict conditions
rdis =np.zeros((nfree,npoin),dtype=np.float64) # Ristricted displacement
fp =np.zeros(nfree*npoin,dtype=np.float64) # External force vector
# section characteristics
for i in range(0,nsec):
text=f.readline()
text=text.strip()
text=text.split()
ae[0,i] =float(text[0]) # E : elastic modulus
ae[1,i] =float(text[1]) # po : Poisson's ratio
ae[2,i] =float(text[2]) # aa : section area
ae[3,i] =float(text[3]) # aix : tortional constant
ae[4,i] =float(text[4]) # aiy : moment of inertia aroutd y-axis
ae[5,i] =float(text[5]) # aiz : moment of inertia around z-axis
ae[6,i] =float(text[6]) # theta : chord angle
ae[7,i] =float(text[7]) # alpha : thermal expansion coefficient
ae[8,i] =float(text[8]) # gamma : unit weight of material
ae[9,i] =float(text[9]) # gkX : acceleration in X-direction
ae[10,i]=float(text[10]) # gkY : acceleration in Y-direction
ae[11,i]=float(text[11]) # gkZ : acceleration in Z-direction
# element-node
for i in range(0,nele):
text=f.readline()
text=text.strip()
text=text.split()
node[0,i]=int(text[0]) #node_1
node[1,i]=int(text[1]) #node_2
node[2,i]=int(text[2]) #section characteristic number
# node coordinates
for i in range(0,npoin):
text=f.readline()
text=text.strip()
text=text.split()
x[0,i]=float(text[0]) # x-coordinate
x[1,i]=float(text[1]) # y-coordinate
x[2,i]=float(text[2]) # z-coordinate
deltaT[i]=float(text[3]) # Temperature change
# boundary conditions (0:free, 1:restricted)
for i in range(0,npfix):
text=f.readline()
text=text.strip()
text=text.split()
lp=int(text[0]) #fixed node
mpfix[0,lp-1]=int(text[1]) #fixed in x-direction
mpfix[1,lp-1]=int(text[2]) #fixed in y-direction
mpfix[2,lp-1]=int(text[3]) #fixed in z-direction
mpfix[3,lp-1]=int(text[4]) #fixed in rotation around x-axis
mpfix[4,lp-1]=int(text[5]) #fixed in rotation around y-axis
mpfix[5,lp-1]=int(text[6]) #fixed in rotation around z-axis
rdis[0,lp-1]=float(text[7]) #fixed displacement in x-direction
rdis[1,lp-1]=float(text[8]) #fixed displacement in y-direction
rdis[2,lp-1]=float(text[9]) #fixed displacement in z-direction
rdis[3,lp-1]=float(text[10]) #fixed rotation around x-axis
rdis[4,lp-1]=float(text[11]) #fixed rotation around y-axis
rdis[5,lp-1]=float(text[12]) #fixed rotation around z-axis
# load
if 0<nlod:
for i in range(0,nlod):
text=f.readline()
text=text.strip()
text=text.split()
lp=int(text[0]) #loaded node
fp[6*lp-6]=float(text[1]) #load in x-direction
fp[6*lp-5]=float(text[2]) #load in y-direction
fp[6*lp-4]=float(text[3]) #load in z-direction
fp[6*lp-3]=float(text[4]) #moment around x-axis
fp[6*lp-2]=float(text[5]) #moment around y-axis
fp[6*lp-1]=float(text[6]) #moment around z-axis
f.close()
return npoin,nele,nsec,npfix,nlod,ae,node,x,deltaT,mpfix,rdis,fp
def prinp_3dfrm(fnameW,npoin,nele,nsec,npfix,nlod,ae,node,x,deltaT,mpfix,rdis,fp):
fout=open(fnameW,'w')
# print out of input data
print('{0:>5s} {1:>5s} {2:>5s} {3:>5s} {4:>5s}'.format('npoin','nele','nsec','npfix','nlod'),file=fout)
print('{0:5d} {1:5d} {2:5d} {3:5d} {4:5d}'.format(npoin,nele,nsec,npfix,nlod),file=fout)
print('{0:>5s} {1:>15s} {2:>15s} {3:>15s} {4:>15s} {5:>15s} {6:>15s} {7:>15s}'
.format('sec','E','po','A','J','Iy','Iz','theta'),file=fout)
print('{0:>5s} {1:>15s} {2:>15s} {3:>15s} {4:>15s} {5:>15s}'
.format('sec','alpha','gamma','gkX','gkY','gkZ'),file=fout)
for i in range(0,nsec):
print('{0:5d} {1:15.7e} {2:15.7e} {3:15.7e} {4:15.7e} {5:15.7e} {6:15.7e} {7:15.7e}'
.format(i+1,ae[0,i],ae[1,i],ae[2,i],ae[3,i],ae[4,i],ae[5,i],ae[6,i]),file=fout)
print('{0:5d} {1:15.7e} {2:15.7e} {3:15.7e} {4:15.7e} {5:15.7e}'
.format(i+1,ae[7,i],ae[8,i],ae[9,i],ae[10,i],ae[11,i]),file=fout)
print('{0:>5s} {1:>15s} {2:>15s} {3:>15s} {4:>15s} {5:>15s} {6:>15s} {7:>15s} {8:>15s} {9:>15s} {10:>15s}'
.format('node','x','y','z','fx','fy','fz','mx','my','mz','deltaT'),file=fout)
for i in range(0,npoin):
lp=i+1
print('{0:5d} {1:15.7e} {2:15.7e} {3:15.7e} {4:15.7e} {5:15.7e} {6:15.7e} {7:15.7e} {8:15.7e} {9:15.7e} {10:15.7e}'
.format(lp,x[0,i],x[1,i],x[2,i],fp[6*lp-6],fp[6*lp-5],fp[6*lp-4],fp[6*lp-3],fp[6*lp-2],fp[6*lp-1],deltaT[i]),file=fout)
print('{0:>5s} {1:>5s} {2:>5s} {3:>5s} {4:>5s} {5:>5s} {6:>5s} {7:>15s} {8:>15s} {9:>15s} {10:>15s} {11:>15s} {12:>15s}'
.format('node','kox','koy','koz','kmx','kmy','kmz','rdis_x','rdis_y','rdis_z','rrot_x','rrot_y','rrot_z'),file=fout)
for i in range(0,npoin):
if 0<mpfix[0,i]+mpfix[1,i]+mpfix[2,i]+mpfix[3,i]+mpfix[4,i]+mpfix[5,i]:
lp=i+1
print('{0:5d} {1:5d} {2:5d} {3:5d} {4:5d} {5:5d} {6:5d} {7:15.7e} {8:15.7e} {9:15.7e} {10:15.7e} {11:15.7e} {12:15.7e}'
.format(lp,mpfix[0,i],mpfix[1,i],mpfix[2,i],mpfix[3,i],mpfix[4,i],mpfix[5,i],rdis[0,i],rdis[1,i],rdis[2,i],rdis[3,i],rdis[4,i],rdis[5,i]),file=fout)
print('{0:>5s} {1:>5s} {2:>5s} {3:>5s}'.format('elem','i','j','sec'),file=fout)
for ne in range(0,nele):
print('{0:5d} {1:5d} {2:5d} {3:5d}'.format(ne+1,node[0,ne],node[1,ne],node[2,ne]),file=fout)
fout.close()
def prout_3dfrm(fnameW,npoin,nele,node,disg,fsec):
fout=open(fnameW,'a')
# displacement
print('{0:>5s} {1:>15s} {2:>15s} {3:>15s} {4:>15s} {5:>15s} {6:>15s}'
.format('node','dis-x','dis-y','dis-z','rot-x','rot-y','rot-z'),file=fout)
for i in range(0,npoin):
lp=i+1
print('{0:5d} {1:15.7e} {2:15.7e} {3:15.7e} {4:15.7e} {5:15.7e} {6:15.7e}'
.format(lp,disg[6*lp-6],disg[6*lp-5],disg[6*lp-4],disg[6*lp-3],disg[6*lp-2],disg[6*lp-1]),file=fout)
# section force
print('{0:>5s} {1:>5s} {2:>15s} {3:>15s} {4:>15s} {5:>15s} {6:>15s} {7:>15s}'
.format('elem','nodei','N_i','Sy_i','Sz_i','Mx_i','My_i','Mz_i'),file=fout)
print('{0:>5s} {1:>5s} {2:>15s} {3:>15s} {4:>15s} {5:>15s} {6:>15s} {7:>15s}'
.format('elem','nodej','N_j','Sy_j','Sz_j','Mx_j','My_j','Mz_j'),file=fout)
for ne in range(0,nele):
print('{0:5d} {1:5d} {2:15.7e} {3:15.7e} {4:15.7e} {5:15.7e} {6:15.7e} {7:15.7e}'
.format(ne+1,node[0,ne],fsec[0,ne],fsec[1,ne],fsec[2,ne],fsec[3,ne],fsec[4,ne],fsec[5,ne]),file=fout)
print('{0:5d} {1:5d} {2:15.7e} {3:15.7e} {4:15.7e} {5:15.7e} {6:15.7e} {7:15.7e}'
.format(ne+1,node[1,ne],fsec[6,ne],fsec[7,ne],fsec[8,ne],fsec[9,ne],fsec[10,ne],fsec[11,ne]),file=fout)
fout.close()
def sm_3dfrm(EA,GJ,EIy,EIz,x1,y1,z1,x2,y2,z2):
ek=np.zeros((12,12),dtype=np.float64) # local stiffness matrix
xx=x2-x1
yy=y2-y1
zz=z2-z1
el=np.sqrt(xx**2+yy**2+zz**2)
ek[ 0, 0]= EA/el
ek[ 0, 6]=-EA/el
ek[ 1, 1]= 12*EIz/el**3
ek[ 1, 5]= 6*EIz/el**2
ek[ 1, 7]=-12*EIz/el**3
ek[ 1,11]= 6*EIz/el**2
ek[ 2, 2]= 12*EIy/el**3
ek[ 2, 4]= -6*EIy/el**2
ek[ 2, 8]=-12*EIy/el**3
ek[ 2,10]= -6*EIy/el**2
ek[ 3, 3]= GJ/el
ek[ 3, 9]=-GJ/el
ek[ 4, 2]= -6*EIy/el**2
ek[ 4, 4]= 4*EIy/el
ek[ 4, 8]= 6*EIy/el**2
ek[ 4,10]= 2*EIy/el
ek[ 5, 1]= 6*EIz/el**2
ek[ 5, 5]= 4*EIz/el
ek[ 5, 7]= -6*EIz/el**2
ek[ 5,11]= 2*EIz/el
ek[ 6, 0]=-EA/el
ek[ 6, 6]= EA/el
ek[ 7, 1]=-12*EIz/el**3
ek[ 7, 5]= -6*EIz/el**2
ek[ 7, 7]= 12*EIz/el**3
ek[ 7,11]= -6*EIz/el**2
ek[ 8, 2]=-12*EIy/el**3
ek[ 8, 4]= 6*EIy/el**2
ek[ 8, 8]= 12*EIy/el**3
ek[ 8,10]= 6*EIy/el**2
ek[ 9, 3]=-GJ/el
ek[ 9, 9]= GJ/el
ek[10, 2]= -6*EIy/el**2
ek[10, 4]= 2*EIy/el
ek[10, 8]= 6*EIy/el**2
ek[10,10]= 4*EIy/el
ek[11, 1]= 6*EIz/el**2
ek[11, 5]= 2*EIz/el
ek[11, 7]= -6*EIz/el**2
ek[11,11]= 4*EIz/el
return ek
def tm_3dfrm(theta,x1,y1,z1,x2,y2,z2):
tt=np.zeros((12,12),dtype=np.float64) # transformation matrix
t1=np.zeros((3,3),dtype=np.float64)
t2=np.zeros((3,3),dtype=np.float64)
xx=x2-x1
yy=y2-y1
zz=z2-z1
el=np.sqrt(xx**2+yy**2+zz**2)
t1[0,0]=1
t1[1,1]= np.cos(theta)
t1[1,2]= np.sin(theta)
t1[2,1]=-np.sin(theta)
t1[2,2]= np.cos(theta)
ll=(x2-x1)/el
mm=(y2-y1)/el
nn=(z2-z1)/el
if x2-x1==0.0 and y2-y1==0.0:
t2[0,2]=nn
t2[1,0]=nn
t2[2,1]=1.0
else:
qq=np.sqrt(ll**2+mm**2)
t2[0,0]=ll
t2[0,1]=mm
t2[0,2]=nn
t2[1,0]=-mm/qq
t2[1,1]= ll/qq
t2[2,0]=-ll*nn/qq
t2[2,1]=-mm*nn/qq
t2[2,2]=qq
t3=np.dot(t1,t2)
tt[0:3,0:3] =t3[0:3,0:3]
tt[3:6,3:6] =t3[0:3,0:3]
tt[6:9,6:9] =t3[0:3,0:3]
tt[9:12,9:12]=t3[0:3,0:3]
return tt
def bfvec_3dfrm(A,gamma,gkX,gkY,gkZ,x1,y1,z1,x2,y2,z2):
# Body force vector in global coordinate system
bfe_g=np.zeros(12,dtype=np.float64)
xx=x2-x1
yy=y2-y1
zz=z2-z1
el=np.sqrt(xx**2+yy**2+zz**2)
bfe_g[0]=0.5*gamma*A*el*gkX
bfe_g[1]=0.5*gamma*A*el*gkY
bfe_g[2]=0.5*gamma*A*el*gkZ
bfe_g[6]=0.5*gamma*A*el*gkX
bfe_g[7]=0.5*gamma*A*el*gkY
bfe_g[8]=0.5*gamma*A*el*gkZ
return bfe_g
def tfvec_3dfrm(EA,alpha,tem):
# Thermal load vector in local coordinate system
tfe_l=np.zeros(12,dtype=np.float64)
tfe_l[0]=-EA*alpha*tem
tfe_l[6]= EA*alpha*tem
return tfe_l
def calsecf_3dfrm(EA,GJ,EIy,EIz,theta,alpha,tem,dis,x1,y1,z1,x2,y2,z2):
ek=sm_3dfrm(EA,GJ,EIy,EIz,x1,y1,z1,x2,y2,z2) # Stiffness matrix in local coordinate
tt=tm_3dfrm(theta,x1,y1,z1,x2,y2,z2) # Transformation matrix
secf=np.dot(ek,np.dot(tt,dis))
secf[0]=secf[0]+EA*alpha*tem
secf[6]=secf[6]-EA*alpha*tem
return secf
def main_3dfrm():
start=time.time()
args = sys.argv
fnameR=args[1] # input data file
fnameW=args[2] # output data file
nod=2 # Number of nodes per element
nfree=6 # Degree of freedom per node
# data input
npoin,nele,nsec,npfix,nlod,ae,node,x,deltaT,mpfix,rdis,fp=inpdata_3dfrm(fnameR,nod,nfree)
# print out of input data
prinp_3dfrm(fnameW,npoin,nele,nsec,npfix,nlod,ae,node,x,deltaT,mpfix,rdis,fp)
# array declaration
ir=np.zeros(nod*nfree,dtype=np.int) # Work vector for matrix assembly
gk=np.zeros((nfree*npoin,nfree*npoin),dtype=np.float64) # Global stiffness matrix
# assembly of stiffness matrix & load vectors
for ne in range(0,nele):
i=node[0,ne]-1
j=node[1,ne]-1
m=node[2,ne]-1
x1=x[0,i]; y1=x[1,i]; z1=x[2,i]
x2=x[0,j]; y2=x[1,j]; z2=x[2,j]
ee =ae[0,m] # elastic modulus
po =ae[1,m] # Poisson's ratio
aa =ae[2,m] # section area
aix =ae[3,m] # tortional constant
aiy =ae[4,m] # moment of inertia around y-axis
aiz =ae[5,m] # moment of inertia around z-axis
theta=np.radians(ae[6,m]) # chord angle
alpha=ae[7,m] # thermal expansion coefficient
gamma=ae[8,m] # unit weight of material
gkX =ae[9,m] # seismic coefficient in X-direction
gkY =ae[10,m] # seismic coefficient in Y-direction
gkZ =ae[11,m] # seismic coefficient in Z-direction
A=aa # section area
EA=ee*aa
GJ=ee/2/(1+po)*aix
EIy=ee*aiy
EIz=ee*aiz
tem=0.5*(deltaT[i]+deltaT[j]) # average temperature change
tt =tm_3dfrm(theta,x1,y1,z1,x2,y2,z2) # Transformation matrix
ek =sm_3dfrm(EA,GJ,EIy,EIz,x1,y1,z1,x2,y2,z2) # Stiffness matrix in local coordinate
ck =np.dot(np.dot(tt.T,ek),tt) # Stiffness matrix in global coordinate
tfe_l=tfvec_3dfrm(EA,alpha,tem) # Thermal load vector in local coordinate
tfe =np.dot(tt.T,tfe_l) # Thermal load vector in global coordinate
bfe =bfvec_3dfrm(A,gamma,gkX,gkY,gkZ,x1,y1,z1,x2,y2,z2) # Body force vector in global coordinate
ir[11]=6*j+5; ir[10]=ir[11]-1; ir[9]=ir[10]-1; ir[8]=ir[9]-1; ir[7]=ir[8]-1; ir[6]=ir[7]-1
ir[5] =6*i+5; ir[4] =ir[5]-1 ; ir[3]=ir[4]-1 ; ir[2]=ir[3]-1; ir[1]=ir[2]-1; ir[0]=ir[1]-1
for i in range(0,nod*nfree):
it=ir[i]
fp[it]=fp[it]+tfe[i]+bfe[i]
for j in range(0,nod*nfree):
jt=ir[j]
gk[it,jt]=gk[it,jt]+ck[i,j]
# treatment of boundary conditions
for i in range(0,npoin):
for j in range(0,nfree):
if mpfix[j,i]==1:
iz=i*nfree+j
fp[iz]=0.0
for i in range(0,npoin):
for j in range(0,nfree):
if mpfix[j,i]==1:
iz=i*nfree+j
fp=fp-rdis[j,i]*gk[:,iz]
gk[:,iz]=0.0
gk[iz,iz]=1.0
# solution of simultaneous linear equations
#disg = np.linalg.solve(gk, fp)
gk = csr_matrix(gk)
disg = spsolve(gk, fp, use_umfpack=True)
# recovery of restricted displacements
for i in range(0,npoin):
for j in range(0,nfree):
if mpfix[j,i]==1:
iz=i*nfree+j
disg[iz]=rdis[j,i]
# calculation of section force
dis=np.zeros(12,dtype=np.float64)
fsec =np.zeros((nod*nfree,nele),dtype=np.float64) # Section force vector
for ne in range(0,nele):
i=node[0,ne]-1
j=node[1,ne]-1
m=node[2,ne]-1
x1=x[0,i]; y1=x[1,i]; z1=x[2,i]
x2=x[0,j]; y2=x[1,j]; z2=x[2,j]
ee =ae[0,m] # elastic modulus
po =ae[1,m] # Poisson's ratio
aa =ae[2,m] # section area
aix =ae[3,m] # tortional constant
aiy =ae[4,m] # moment of inertia around y-axis
aiz =ae[5,m] # moment of inertia around z-axis
theta=np.radians(ae[6,m]) # chord angle
alpha=ae[7,m] # thermal expansion coefficient
EA=ee*aa
GJ=ee/2/(1+po)*aix
EIy=ee*aiy
EIz=ee*aiz
tem=0.5*(deltaT[i]+deltaT[j]) # average temperature change
dis[0]=disg[6*i] ; dis[1] =disg[6*i+1]; dis[2]= disg[6*i+2]
dis[3]=disg[6*i+3]; dis[4] =disg[6*i+4]; dis[5]= disg[6*i+5]
dis[6]=disg[6*j] ; dis[7] =disg[6*j+1]; dis[8]= disg[6*j+2]
dis[9]=disg[6*j+3]; dis[10]=disg[6*j+4]; dis[11]=disg[6*j+5]
fsec[:,ne]=calsecf_3dfrm(EA,GJ,EIy,EIz,theta,alpha,tem,dis,x1,y1,z1,x2,y2,z2)
# print out of result
prout_3dfrm(fnameW,npoin,nele,node,disg,fsec)
# information
dtime=time.time()-start
print('n={0} time={1:.3f}'.format(nfree*npoin,dtime)+' sec')
fout=open(fnameW,'a')
print('n={0} time={1:.3f}'.format(nfree*npoin,dtime)+' sec',file=fout)
fout.close()
# ==============
# Execution
# ==============
if __name__ == '__main__': main_3dfrm()
以 上