Pythonで作成した軸対称応力解析プログラムの適用事例です.
理論解
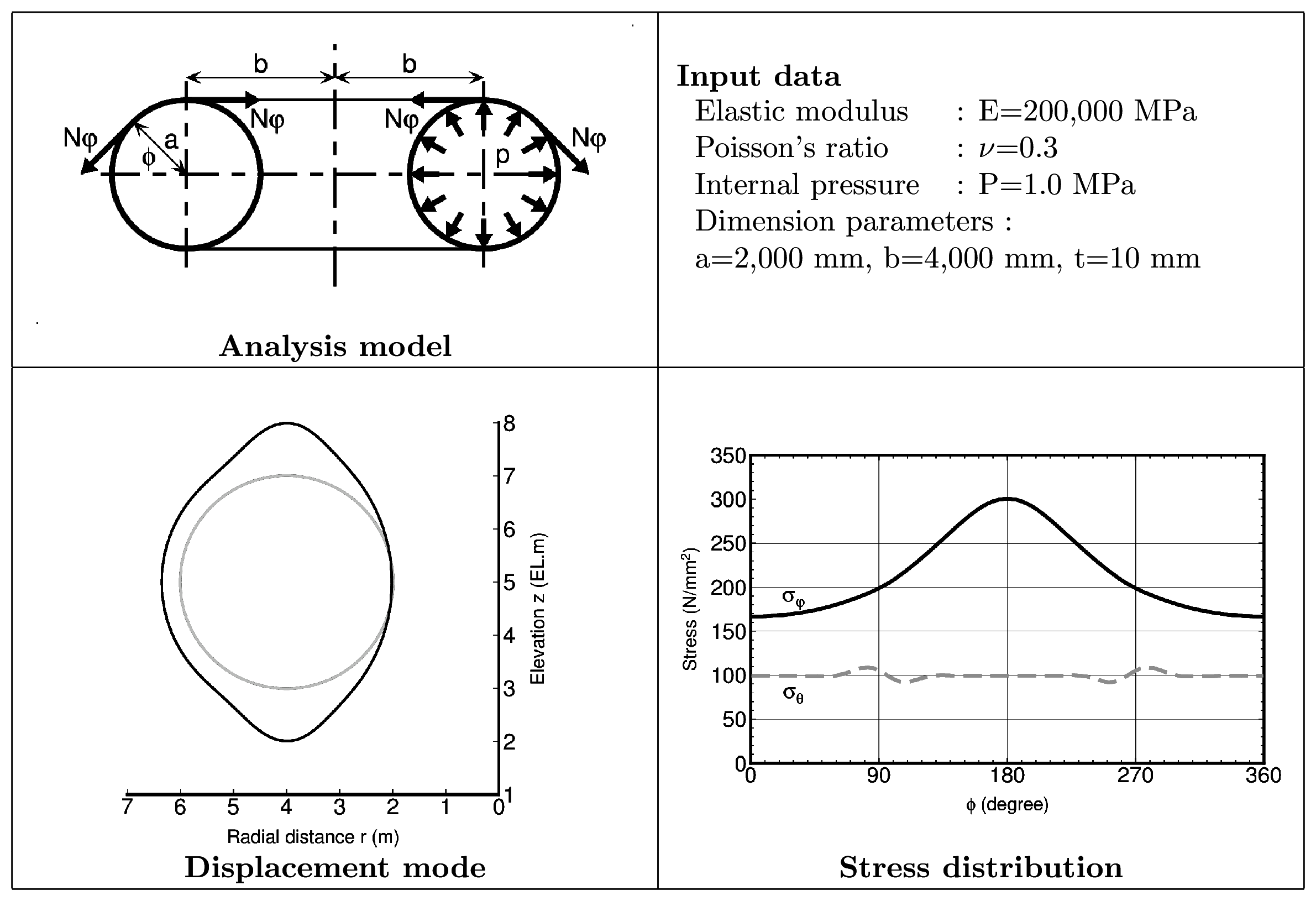
トーラス(トロイダル・シェル)とは,下図左に示すように,円環を中心軸(ここでは鉛直軸)の回りに回転させた,ドーナツ状の立体である.
上図右に示すように,均等内圧 p を受けるトーラスを考える.この場合,半径 a の円周方向軸力 $N_{\varphi}$ およびその軸方向軸力 $N_{\theta}$ は,Timoshenko (Theory of Plates and Shells) により,次式で与えられている.
$$
\begin{equation*}
N_{\varphi}=\cfrac{p a (r_0 + b)}{2 r_0} \qquad\qquad N_{\theta}=\cfrac{p a}{2}
\end{equation*}
$$
上式より,$N_{\varphi}$ は場所により変化するが,$N_{\theta}$ は,半径 a の円環上で均一な値をとることが分かる.
ここで,代表点での$N_{\varphi}$を書き直してみると,
$$
\begin{align*}
&N_{\varphi}=p a \left\{1 + \cfrac{a}{2(b - a)}\right\} & (r_0 = b - a) \
&N_{\varphi}=p a & (r_0 = b) \
&N_{\varphi}=p a \left\{1 - \cfrac{a}{2(b + a)}\right\} & (r_0 = b + a)
\end{align*}
$$
となり,円環の内側,すなわち回転軸側 ($r_0 = b - a$) の円周方向応力が大きくなることがわかる.
また,半径 a の円環の頂部と底部の円周方向応力は,通常の均等内水圧を受ける半径 a の直線円環の周方向軸力と同じ値となる.
軸対称FEMによる解析
以下に示すトーラスの発生応力を,軸対称FEM解析にて予測した.解析条件は以下のとおり.ここに,t はトーラスを構成する材料の板厚を示す.
| E (MPa) | po | p (MPa) | a (mm) | b (mm) | t (mm) |
|---|---|---|---|---|---|
| 200,000 | 0.3 | 1.0 | 2,000 | 4,000 | 10 |
| 要素数:360 (半径 a の円を中心角 1 度で分割) | |||||
軸対称FEMでは荷重は回転軸に対し 1 rad あたりの荷重を入力するようになっている.水圧についても例外ではなく,定義に忠実に荷重を作成・入力する必要があることに注意.
上図右下の応力分布図において,
水平軸の角度は,変位図を参照して,
トーラス外側最外点(水平左端)をゼロとして,頂部が90度,回転軸側最内点が180度,底部が270度としている.
解析結果と Timoshenko の解との比較を下表に示す.
| Location | FEM | Timoshenko | ||
|---|---|---|---|---|
| (φ) | σφ | σθ | σφ | σθ |
| 0 (r=b+a) | 166.59 | 99.54 | 166.66 | 100.00 |
| 90 (r=b) | 198.43 | 105.62 | 200.00 | 100.00 |
| 180 (r=b-a) | 300.54 | 99.55 | 300.00 | 100.00 |
| 応力の単位は MPa | ||||
プログラム
プログラムはGistへのリンクで示します.
- 軸対称FEM解析プログラム (py_fem_asnt.py)
- 作図用データ作成プログラム (py_fig_data.py)
- GMTによる変位モード・応力分布図作成スクリプト (a_gmt_gra.txt)
- トーラスモデル作成スクリプト (a_gmt_model.txt)
- トーラス解析用入力データ (inp_torus.txt)
- gnuplotによるトーラス作図スクリプト (gpl_torus.txt)
以 上