プログラムとしての仕上がりは下の投稿のほうがいいと思いますので参考にしていただければと思います.
概要
Pythonによる線形弾性2次元FEM応力解析プログラムを作ってみた.
要素は,1要素4節点のアイソパラメトリック要素であり,1要素に4ガウス積分点を持つ.
扱える荷重は以下の通り.
- 節点外力
- 節点温度変化
- 自重および地震時慣性力
理論式
節点変位計算式
$$
[\boldsymbol{k}]\{\boldsymbol{u}\}=\{\boldsymbol{f}\}+\{\boldsymbol{f_t}\}+\{\boldsymbol{f_b}\}
$$
$$
\begin{align}
&[\boldsymbol{k}]=t\cdot \int_A [\boldsymbol{B}]^T[\boldsymbol{D}][\boldsymbol{B}] dA \
&\{\boldsymbol{f_t}\}=t\cdot \int_A [\boldsymbol{B}]^T[\boldsymbol{D}]\{\boldsymbol{\epsilon_0}\} dA \
&\{\boldsymbol{f_b}\}=t\cdot\gamma\cdot \int_A [\boldsymbol{N}]^T [\boldsymbol{N}] dA \cdot \{\boldsymbol{w}\}
\end{align}
$$
- $[\boldsymbol{k}]$ : 要素剛性マトリックス
- $\{\boldsymbol{u}\}$ : 節点変位ベクトル
- $\{\boldsymbol{f}\}$ : 節点外力ベクトル
- $\{\boldsymbol{f_t}\}$ : 温度変化による節点力ベクトル
- $\{\boldsymbol{f_b}\}$ : 自重・地震加速度による節点ベクトル
- $[\boldsymbol{D}]$ : 応力ー歪関係マトリックス
- $t$, $\gamma$ : 要素厚さ,要素単位体積重量
- $\{\boldsymbol{w}\}$ : 節点加速度ベクトル(重力加速度に対する比率で入力)
要素応力算定式
$$
\{\boldsymbol{\sigma}\}=[\boldsymbol{D}]\{\boldsymbol{\epsilon}-\boldsymbol{\epsilon_0}\}
$$
$\{\boldsymbol{\epsilon_0}\}$は,温度変化による歪
節点変位ー任意位置ひずみ関係式
$$
\{\boldsymbol{\epsilon}\}=[\boldsymbol{B}]\{\boldsymbol{u}\}
$$
$\{\boldsymbol{\epsilon}\}$は,要素内任意点の歪
節点変位ー任意位置歪算定式
$$
\{\boldsymbol{v}\}=[\boldsymbol{N}]\{\boldsymbol{u}\}
$$
$\{\boldsymbol{v}\}$は,要素内任意点の変位
使えるか?
Pythonはインタプリタなので,計算速度的に使い物になるか不安であったが,節点数:3417,要素数:3257,自由度:6834のモデルでの計算時間は,7.9秒であり,使えるレベルであることが確認できた.
プログラム
プログラムは,長いので,Gistに貼り付けたものにリンクを貼っています.
なお,コンター作図といっても,要素を応力レベルに応じて色分けして塗りつぶしているだけです.私の目的では別に内挿してコンターラインを引いて貰う必要はないため.
- 2次元FEM応力解析プログラム(py_fem_plnt.py)
- 主応力コンター作図プログラム(py_fig_cont.py)
- 主応力ベクトル&変位モード作図プログラム(py_fig_vect.py)
- 3417節点モデルの入力データ(inp_arch.txt)
入力データフォーマット
npoin nele nsec npfix nlod NSTR # 基本量
t E po alpha gamma gkh gkv # 材料特性
..... (1~nsec) .....
node1 node2 node3 node4 isec # 要素-節点関係,材料特性番号
..... (1~nele) .....
x y deltaT # 節点座標,節点温度変化
..... (1~npoin) .....
node kox koy rdisx rdisy # 変位拘束条件
..... (1~npfix) .....
node fx fy # 外力
..... (1~nlod) .....
| npoin, nele, nsec | 節点数,要素数,材料特性数 |
| npfix, nlod | 拘束節点数,載荷節点数 |
| NSTR | 応力状態(平面歪:0,平面応力:1) |
| t, E, po, alpha | 板厚,弾性係数,ポアソン比,線膨張係数 |
| gamma, gkh, gkv | 単位体積重量,水平及び鉛直方向加速度(gの比) |
| x, y, deltaT | 節点x座標,節点y座標,節点温度変化 |
| node, kox, koy | 拘束節点番号,x及びy方向拘束の有無(拘束:1,自由:0) |
| rdisx, rdisy | x及びy方向変位(無拘束でも0を入力) |
| node, fx, fy | 載荷重節点番号,x方向荷重,y方向荷重 |
出力データフォーマット
npoin nele nsec npfix nlod NSTR
4 1 1 2 2 1
sec t E po alpha gamma gkh gkv
1 1.0000000e+00 1.0000000e+03 0.0000000e+00 1.0000000e-05 2.3000000e+00 0.000 0.000
node x y fx fy deltaT kox koy
1 0.0000000e+00 0.0000000e+00 0.0000000e+00 0.0000000e+00 0.0000000e+00 1 1
2 1.0000000e+00 0.0000000e+00 0.0000000e+00 0.0000000e+00 0.0000000e+00 0 1
3 1.0000000e+00 1.0000000e+00 0.0000000e+00 1.0000000e+01 0.0000000e+00 0 0
4 0.0000000e+00 1.0000000e+00 0.0000000e+00 1.0000000e+01 0.0000000e+00 0 0
node kox koy rdis_x rdis_y
1 1 1 0.0000000e+00 0.0000000e+00
2 0 1 0.0000000e+00 0.0000000e+00
elem i j k l sec
1 1 2 3 4 1
node dis-x dis-y
1 0.0000000e+00 0.0000000e+00
2 8.8817842e-19 0.0000000e+00
3 1.7763568e-18 2.0000000e-02
4 4.1448326e-18 2.0000000e-02
elem sig_x sig_y tau_xy p1 p2 ang
1 -7.4014868e-16 2.0000000e+01 1.1333527e-16 2.0000000e+01 0.0000000e+00 9.0000000e+01
n=8 time=0.044 sec
| node, dis-x, dis-y | 節点番号,x方向変位,y方向変位 |
| elme, sig_x, sig_y, tau_xy | 要素番号,x方向直応力,y方向直応力,せん断応力 |
| p1, p2, ang | 第一主応力,第二主応力,第一主応力の方向 |
| n, time | 全自由度,計算時間 |
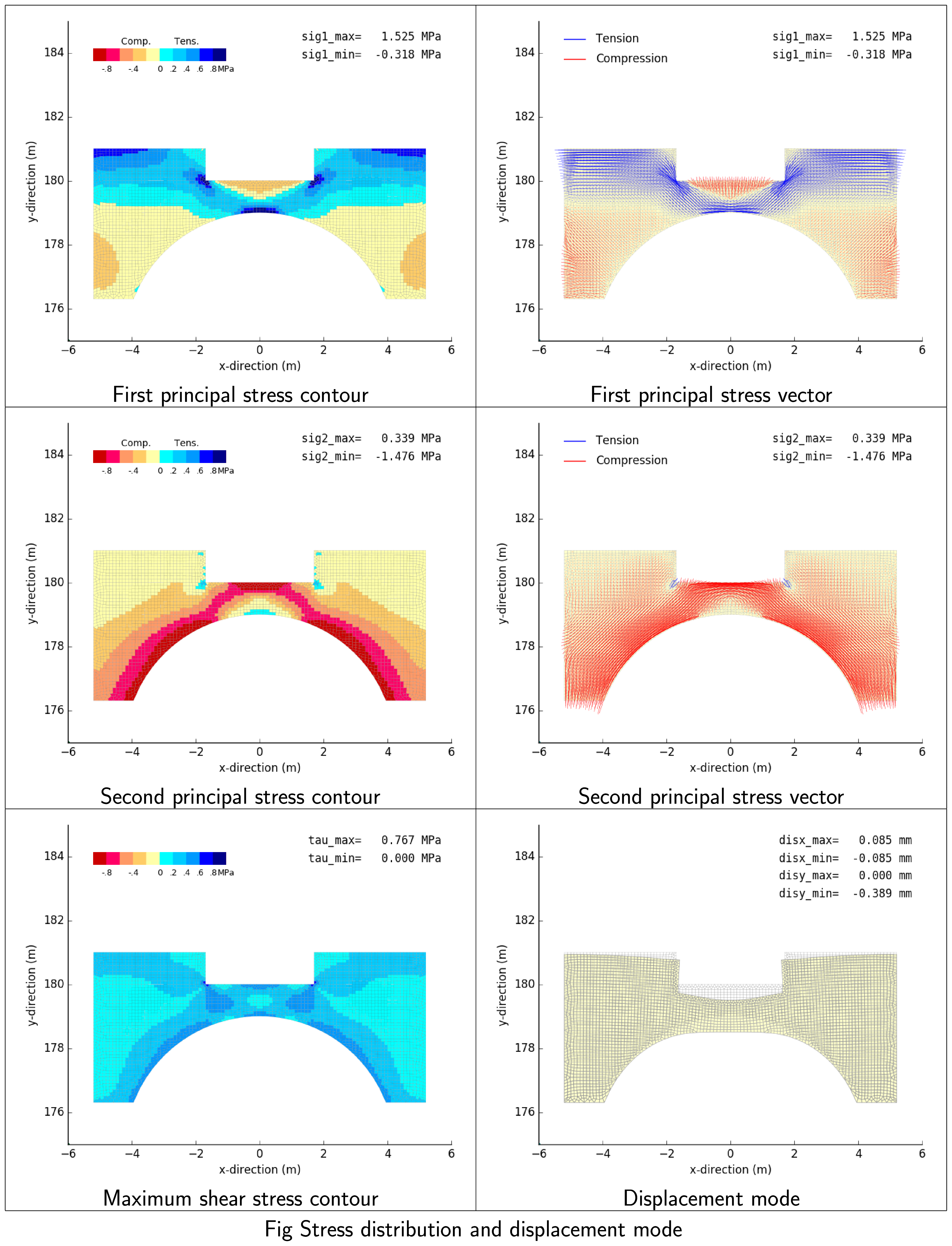
出力事例
以 上