LoginSignup
5
3

More than 5 years have passed since last update.

@damyarou

Pythonで２次元飽和ー不飽和浸透流解析

Last updated at Posted at 2016-11-24

(2017.11.19 修正)

一部プログラムミスがあったためプログラムを修正

概要

ざっくりとした感想

２次元FEM応力解析プログラムを作ったので，ついでに，２次元飽和ー不飽和浸透流解析プログラムを作ってみた．
要素は，２次元応力解析と同じく，１要素４節点４ガウス積分点を有するアイソパラメトリック要素である．

実際の所，使えるかであるが，節点数１３１７，要素数１２２７，収束計算回数10回で，計算時間3.7秒であり，この程度の規模の問題であれば，特にストレスを感じることはない．
Numpyの行列演算と，連立一次方程式を解くルーチンが優秀なのだろう．

プログラムする上で心がけた事項は以下の通り．

  • 配列は全てNumpy配列とする．リストは用いない．
  • forの使用は極力避け，Numpyの行列演算を用いる．ただし１次元ベクトルの積などで予期せぬ結果となる場合があるので注意を要する
  • 連立一次方程式を解くには，x=numpy.linalg.solve(A, b)で十分．境界条件処理により，行列は非対称となるので，コレスキー分解などはどっちみち使えない．
  • 上記を行うことで，プログラム本体の見通しは非常に良くなる
  • 入出力部が，ごちゃごちゃしてしまうが，これは避けられないことか？

飽和浸透流解析

飽和定常浸透流解析は，以下の連立一次方程式を解く問題である．

$$
[k]\{h\}=\{q\}
$$

$$
\begin{bmatrix}k_{11} & k_{12} & \dots \\
k_{21} & k_{22} & \dots \\
\dots & \dots & \dots \\
\dots & \dots & k_{nn}\end{bmatrix}
\begin{Bmatrix}h_1 \\ h_2 \\ \dots \\ h_n \end{Bmatrix}
=\begin{Bmatrix}q_1 \\ q_2 \\ \dots \\ q_n \end{Bmatrix}
$$

$$
\begin{bmatrix}k_{11} & k_{12} & \dots \\
k_{21} & k_{22} & \dots \\
\dots & \dots & \dots \\
\dots & \dots & k_{nn}\end{bmatrix}
\begin{Bmatrix}h_{\text{unknown}} \\ h_{\text{unknown}} \\ \dots \\ h_{\text{given}} \end{Bmatrix}
=\begin{Bmatrix}q_{\text{given}} \\ q_{\text{given}} \\ \dots \\ q_{\text{unknown}} \end{Bmatrix}
$$

ここで，$\{q\}$は節点流量ベクトル，$\{h\}$は全水頭ベクトル，$[k]$は透水行列であり，以下の特性を有する．

  • 透水行列$[k]$は定数，
  • 節点流量ベクトル$\{q\}$の既知成分に相当する全水頭ベクトル$\{h\}$は未知数
  • 節点流量ベクトル$\{q\}$の未知成分に相当する全水頭ベクトル$\{h\}$は既知数

このため，既知数と未知数の関係の処理を行った後，一回連立方程式を解くことにより解が得られる．

(連立一次方程式を解くための既知数と未知数の関係の処理)

$q_i$，$q_j$を除く流量および $h_i$，$h_j$ が既知,$h_i$，$h_j$ を除く全水頭および $q_i$，$q_j$ が未知とすれば，透水マトリックスの $k_{ii}$ および $k_{jj}$ を $1$ とし，それ以外の $i$ 列および $j$ 列の要素をゼロとする処理を行う．また透水マトリックスにおける $i$ 列および $j$ 列の効果を右辺に移項する．

$$
\begin{bmatrix}
k_{11} & \ldots & 0 & \ldots & 0 & \ldots & k_{1n} \\
\vdots & \ddots & \vdots & \ddots & \vdots & \ddots & \vdots \\
k_{i1} & \ldots & 1 & \ldots & 0 & \ldots & k_{in} \\
\vdots & \ddots & \vdots & \ddots & \vdots & \ddots & \vdots \\
k_{j1} & \ldots & 0 & \ldots & 1 & \ldots & k_{jn} \\
\vdots & \ddots & \vdots & \ddots & \vdots & \ddots & \vdots \\
k_{n1} & \ldots & 0 & \ldots & 0 & \ldots & k_{nn}
\end{bmatrix}
\begin{Bmatrix}
h_1 \\
\vdots \\
-q_i \\
\vdots \\
-q_j \\
\vdots \\
h_n
\end{Bmatrix}
=\begin{Bmatrix}
q_1 \\
\vdots \\
0 \\
\vdots \\
0 \\
\vdots \\
q_n
\end{Bmatrix}
-h_i
\begin{Bmatrix}
k_{1i} \\
\vdots \\
k_{ii} \\
\vdots \\
k_{ji} \\
\vdots \\
k_{ni}
\end{Bmatrix}
-h_j
\begin{Bmatrix}
k_{1j} \\
\vdots \\
k_{ij} \\
\vdots \\
k_{jj} \\
\vdots \\
k_{nj}
\end{Bmatrix}
$$

飽和-不飽和浸透流解析

飽和-不飽和浸透流解析での連立方程式は，以下の特性を有する．

  • 境界条件には，流量既知，全水頭既知，浸潤面が出現する境界の3種類を考慮する必要がある．
  • 浸潤面が出現する境界以外は，流量か全水頭のいずれかが既知となる．
  • 浸潤面が出現する境界上では流量・全水頭とも未知数となる．
  • ただし浸潤面が出現する境界は，基本的に大気に接する境界であるため，雨の流入などを考慮しなければ流量は流出のみ(プログラム上は0以下)， 圧力水頭も0以下という制約がある．
  • 飽和領域での透水行列の成分は定数であるが，不飽和領域での透水行列の成分はサクション圧(負の圧力水頭)の関数となっている．

このため，収束計算により，未知数を定める必要がある．
収束計算の方法は，全節点に全水頭の初期値を与え，得られた解を次の収束計算の入力値とする，逐次代入法とした．この方法は，全節点の水頭を仮定するため，全要素の透水行列を仮定した水頭から設定でき，計算フローを単純化できる．
全水頭の初期値は，全水頭既知境界以外は，飽和領域の最小全水頭を与えるのが，解の精度・収束性を考慮したうえで有効のようである．

不飽和透水特性（van Genuchten モデル）

地盤の不飽和透水特性モデルは，飽和度-サクション圧関係，飽和度-不飽和透水係数比をテーブルで入力する方法もあるが，解析上，連続関数で取り扱うほうが，プログラムが単純化できるため，van Genuchten モデルを採用した．

$$
S_e=\left\{\frac{1}{1+\left(\alpha\cdot h_s\right)^n}\right\}^m \qquad n=\frac{1}{1-m} \quad (0<m<1)
$$

$$
K_r=(S_e)^{0.5}\cdot\left\{1-\left(1-S_e{}^{1/m}\right)^m\right\}^2 \qquad (0 \leqq S_r, K_r \leqq 1)
$$

$$
K=K_r \cdot K_0
$$

  • $S_e$ : Degree of saturation
  • $K_r$ : Relative hydraulic conductivity function
  • $h_s$ : Suction head
  • $\alpha$ : Scaling parameter
  • $m$ : Non-dimensional parameter
  • $K$ : Permiability coefficient
  • $K_0$ : Saturated permiability coefficient

プログラム

プログラムを載せると長くなるので，自分のHPへのリンクを貼っておく．

入力データ・フォーマット

npoin  nele  nsec  koh  koq  kou  idan
Ak0  alpha  em
..... (1~nsec) .....
node-1  node-2  node-3  node-4  isec
..... (1~nele) .....
x  z  hvec0
..... (1~npoin) .....
nokh  Hinp
..... (1~koh) .....
nokq  Qinp
..... (1~koq) .....
noku
..... (1~kou) .....
npoin, nele, nsec 節点数，要素数，材料特性数
koh, koq, kou 水頭指定節点数，流量指定節点数，浸潤境界節点数
idan 解析断面（０：鉛直断面，１：水平断面）
Ak0 要素の飽和透水係数
alpa, em 要素の不飽和透水特性
node-1, node-2, node-3, node-4, isec 要素を構成する節点番号，要素の材料特性番号
x, z, hvec0 節点のxおよびz座標，収束計算用初期水頭値
nokh, Hinp 水頭指定節点番号および水頭値
nokq, Qinp 流量指定節点番号および流量値
noku 浸潤境界節点番号

出力データ・フォーマット

npoin  nele  nsec   koh   koq   kou  idan
    9     4     1     6     0     0     1
  sec             Ak0           alpha              em
    1   1.0000000e-05   0.0000000e+00   0.0000000e+00
 node               x               z            hvec            qvec   koh   koq   kou
    1   0.0000000e+00   0.0000000e+00   1.0000000e+01   0.0000000e+00     1     0     0
    2   1.0000000e+00   0.0000000e+00   1.0000000e+01   0.0000000e+00     1     0     0
    3   2.0000000e+00   0.0000000e+00   1.0000000e+01   0.0000000e+00     1     0     0
    4   0.0000000e+00   1.0000000e+00   0.0000000e+00   0.0000000e+00     0     0     0
    5   1.0000000e+00   1.0000000e+00   0.0000000e+00   0.0000000e+00     0     0     0
    6   2.0000000e+00   1.0000000e+00   0.0000000e+00   0.0000000e+00     0     0     0
    7   0.0000000e+00   2.0000000e+00   0.0000000e+00   0.0000000e+00     1     0     0
    8   1.0000000e+00   2.0000000e+00   0.0000000e+00   0.0000000e+00     1     0     0
    9   2.0000000e+00   2.0000000e+00   0.0000000e+00   0.0000000e+00     1     0     0
 node  Hinp
    1   1.0000000e+01
    2   1.0000000e+01
    3   1.0000000e+01
    7   0.0000000e+00
    8   0.0000000e+00
    9   0.0000000e+00
 elem     i     j     k     l   sec
    1     1     2     5     4     1
    2     2     3     6     5     1
    3     4     5     8     7     1
    4     5     6     9     8     1
 node            hvec            pvec            qvec   koh   koq   kou
    1   1.0000000e+01   1.0000000e+01   2.5000000e-05     1     0     0
    2   1.0000000e+01   1.0000000e+01   5.0000000e-05     1     0     0
    3   1.0000000e+01   1.0000000e+01   2.5000000e-05     1     0     0
    4   5.0000000e+00   5.0000000e+00  -6.7762636e-21     0     0     0
    5   5.0000000e+00   5.0000000e+00   2.7105054e-20     0     0     0
    6   5.0000000e+00   5.0000000e+00   0.0000000e+00     0     0     0
    7   0.0000000e+00   0.0000000e+00  -2.5000000e-05     1     0     0
    8   0.0000000e+00   0.0000000e+00  -5.0000000e-05     1     0     0
    9   0.0000000e+00   0.0000000e+00  -2.5000000e-05     1     0     0
 elem              vx              vz              vm              kr
    1  -5.5511151e-21   5.0000000e-05   5.0000000e-05   1.0000000e+00
    2   5.5511151e-21   5.0000000e-05   5.0000000e-05   1.0000000e+00
    3  -5.5511151e-21   5.0000000e-05   5.0000000e-05   1.0000000e+00
    4   5.5511151e-21   5.0000000e-05   5.0000000e-05   1.0000000e+00
Total inflow =  1.0000000e-04
Total outflow= -1.0000000e-04
Max.velocity in all area     =  5.0000000e-05 (ne=1)
Max.velocity in inflow area  =  5.0000000e-05 (ne=1)
Max.velocity in outflow area =  5.0000000e-05 (ne=3)
iii=2  icount=9  kop=0
n=9  time=0.007 sec
node, hvec, pvec, qvec 節点番号，全水頭，圧力水頭，流量
elem, vx, vz, vm 要素のx・z方向流速および合成流速
Kr 要素の不飽和透水特性（１：飽和，１＞：不飽和）
Total inflow, Total outflow モデル領域への全流入量および全流出量
iii, icount 収束計算回数，計算完了条件を満たす自由度数
kop 浸潤面境界節点のうち圧力水頭が０となる節点数
n, time 全自由度，計算時間

出力事例

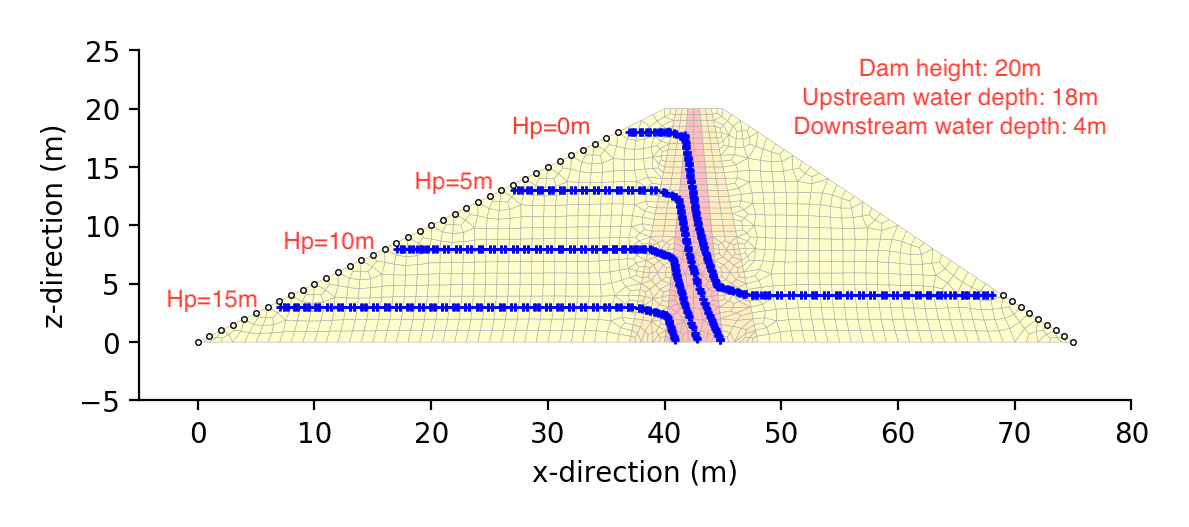
簡易コンター作成プログラムにより，圧力水頭０， ５， １０， １５ｍのコンターを引いてみた図．
上流側では高さ18m，下流側では高さ4mの水深を与えている．
コンター図そのものは，素人レベルのものであるが，計算はうまく回っているようである．
なお，赤字で示した圧力水頭やダム諸元は，MacのPreviewで追加書きしたものである．

ここらへんの作図は，GMT(Generic Mapping Tools)のコンター機能に任せて作図したほうが，報告書用としては見栄えがする．

ちなみに，実際のダムでは，コアとフィルターの境界付近で圧力水頭の低下が発生し，解析結果に示すようにコア内部での圧力低下は起こらないことは，周知の事実である．
あくまでも，解析事例ということで，理解いただきたい．

_fig_seep4_cont.png

以　上

5
3
5

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
5
3