本記事は42tokyoアドベントカレンダーの9日目の記事になります!
(昨日は狩野達哉さん、スタートアップに関する基本的な知識パターンでした。とても勉強になったので読んでみてください)
はじめに
10月からフランス発の謎のエンジニア養成機関42tokyoで学んでいます。
先生、メンターの類はおらず、自力で調べ、生徒どうし教え、教わりながら日々課題に取り組んでいます。鬼の自走力が身に付くよい環境だと思います。
その課題(の結構序盤に)C言語のprintf関数を作りましょうというけっこう骨太な課題があります。charやらintやらの出力は割と簡単にできるのですが、double(倍精度浮動小数点型)の出力で結構てこずったので、このアドベントの機会にまとめておこうと思います。浮動小数点型を理解したい方や、これからprintfの課題に取り組む42生のお役に立てれば幸いです。(ちなみに、doubleの出力はボーナスパートです。)
なお、ググれどもググれどもなかなかいい情報が見つかりませんでしたので、本記事の内容は完全な自己流になります。間違いや改善点などあれば教えていただけますと幸いです。
完全なソースコードはgithub(https://github.com/dai65527/putfloat )にあります。
この記事のゴール
以下のことができることを本記事のゴールとします。
- 出力に使用するのはシステムコール関数のwriteのみ。
- float型(単精度浮動小数点型、32bit)を対象にする。
- 整数部23桁、小数部149桁を標準出力に出力する(桁数については後述)。
- 本家printfと出力が合うようにする。
printfではdouble型(倍精度浮動小数点型、64bit)しか扱いませんが、今回は解説のしやすさ(単に桁が少ないだけですが)からfloat型(単精度浮動小数点型、32bit)型を対象にします。また、実際のprintfでは桁数を切って丸めて出力するのが基本なのですが、今回は扱いません。
IEEE754形式の浮動小数点
だいたいの環境ですと、浮動小数点を表すのにIEEE754形式が用いられています(wiki)
まずはそれを理解するところからスタートです。
そもそも浮動小数点数とは
浮動小数点数は、以下のような形式で表されている実数(含む小数)です。
(浮動小数点数)=(-1)^{(符号)} ×(仮数)×(基数)^{(指数)}
例えば、10進数の123.456は次のように表します。
123.456=(-1)^0×1.23456×10^2
上の例を見るとわかりやすいですが、浮動小数点数は以下の4つの情報で表すことができます。
- 符号:0なら正1なら負。
- 仮数:0以上で基数より小さい数。
- 基数:n進数のnに当たる部分。
- 指数:基数の何乗か。いわゆるオーダー。
基数のn乗という表現を使うことで、少ない情報で量でとても大きな数字から、小さな数字までを扱うことができます。
IEEE754の表現
コンピュータにおいて浮動小数点数を扱う際は、上記の浮動小数点数の各情報は有限のbit数の中に保持されます。今回扱うIEEE754の規格の単精度浮動小数点型(32bit、C言語のfloat型)では、下の図のように保存されています(wikiより拝借)。

もちろん基数は2になります。これはそのまま先ほどのような式にはあてはめられず、指数、仮数については少し工夫がされています。
指数のバイアス
指数部は8bit、つまり0から255(=2^8-1)までの幅を持っています。ここで、0と255は特別な意味を持つ(後述)ので、実際に指数として使うのは1から254です。そして、負の数を表す必要があるため、この値から127を引いた-126から127までが実際の指数になります。この127という数字をバイアスと呼びます。
仮数のケチ表現
仮数は23bit分の情報をもっていますが、基本的に最上位bitは常に1になる(1.010...×2^nの形になる)ため、最上位bitに1を追加した、計24bitとして扱います。これをケチ表現といいます。24bitを1bitケチって23bitで保存しているからケチってことですね。
指数のバイアスと仮数のケチ表現を考慮すると、IEEE754の浮動小数点型以下のような浮動小数点の形式で表すことができます。
(浮動小数点数)=(-1)^{(符号)} ×(1.仮数)_{(2)}×2^{(指数-127)}
先ほどの画像に当てはめると以下のようになります。添え字の(2)は2進数という意味です。
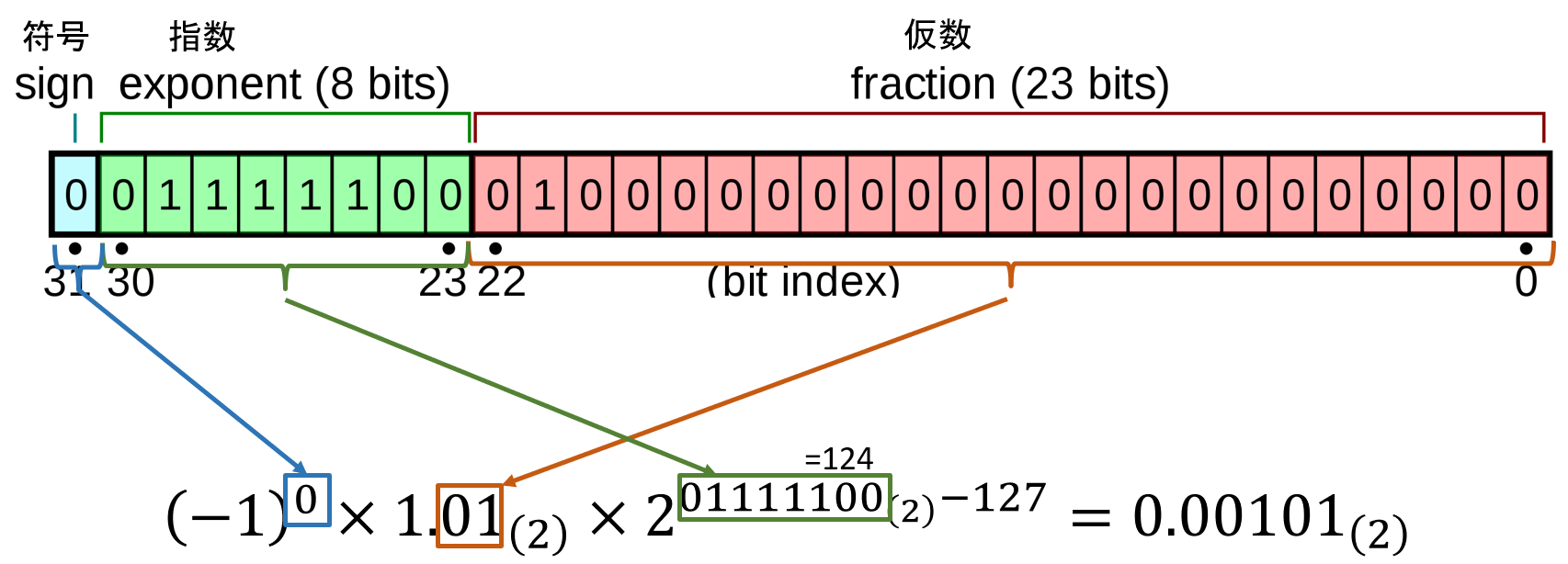
指数部が0のとき(0と非正規数)
先ほど述べましたが、指数部が0の場合は特別な意味になります。この場合はケチ表現を使わずに、仮数部23ビットをそのまま仮数とします。このように表す数を非正規数といいます。逆にケチ表現を用いている場合を正規数といいます。非正規数を用いることで、正規数の最小値(1×2^-126)よりも0に近い値を表現することができます。
また、**仮数部も0の場合は0(ゼロ)**をあらわしています。なお、指数部と仮数部が0でも符号部は0と1がとることができるため、浮動小数点型のゼロには「0」と「-0」があります。
指数部が255のとき(infとnan)
指数部が255(最大値)の場合も特別な意味を持ちます。
- 仮数部が0:inf (無限大)
- 仮数部が0以外:nan(not a number)
inf(無限大)は0以外の数を0で割った場合など、nanは負の平方根や0を0で割った場合などに発生します。これも0の場合と同様に符号を持てます(「-inf」と「inf」がある)。nanの符号は無視されたりされなかったり処理系依存のようです。(https://ja.wikipedia.org/wiki/NaN )
IEEE754のまとめ
上記の話をまとめると次のようになります。
| 種類 | 指数部 | 仮数部 |
|---|---|---|
| ゼロ | 0 | 0 |
| 非正規数 | 0 | 0以外(非ケチ表現) |
| 正規数 | 1~254 | 任意(ケチ表現) |
| inf | 255 | 0 |
| nan | 255 | 0以外 |
浮動小数点型を出力するまでの流れ
浮動小数点型がコンピュータ上でどのように表されるかがわかったところで、次は実際に出力するところを考えていきます。大まかに以下の流れで行います。
- 符号部、指数部、仮数部を別々の変数に取り出す。
- 2進数を10進数の形式に変換する。
- 10進数を標準出力へ出力する。
関数printfloatに直すと以下のような感じですね。floatの情報を格納する構造体s_ifloatを定義して使用します。
void printfloat(float num)
{
struct s_ifloat ifloat;
ifloat = store_ifloat(num); // 符号部、指数部、仮数部を別々の変数に取り出す
convert_ifloat(&ifloat); // 2進数->10進数へ変換
print_ifloat(ifloat); // 標準出力へ出力
}
1. 符号部、指数部、仮数部の取り出し
まず、float型の変数からIEEE754の形式に沿って格納されている符号部、指数部、仮数部を取り出します。(必ずしも取り出さなくても良いのですが、取り出したほうが操作しやすいので取り出します)
取り出した情報を格納するための構造体s_ifloatを以下のように定義します。
struct s_ifloat
{
uint8_t sign; // 符号1bitを収納
uint8_t exp; // 指数部8bitを収納
uint32_t frac; // 仮数部23bitを収納
};
それぞれ、以下の図のようなイメージで保存します。指数部signは最下位ビットの方につめてそのまま使えます。指数部は8bitちょうどなのでそのまま詰め込みます。仮数部は23bitに対して32bitあるのですが、上位bit側につめて使います。(そちらの方が個人的に使い勝手がよかったため。)
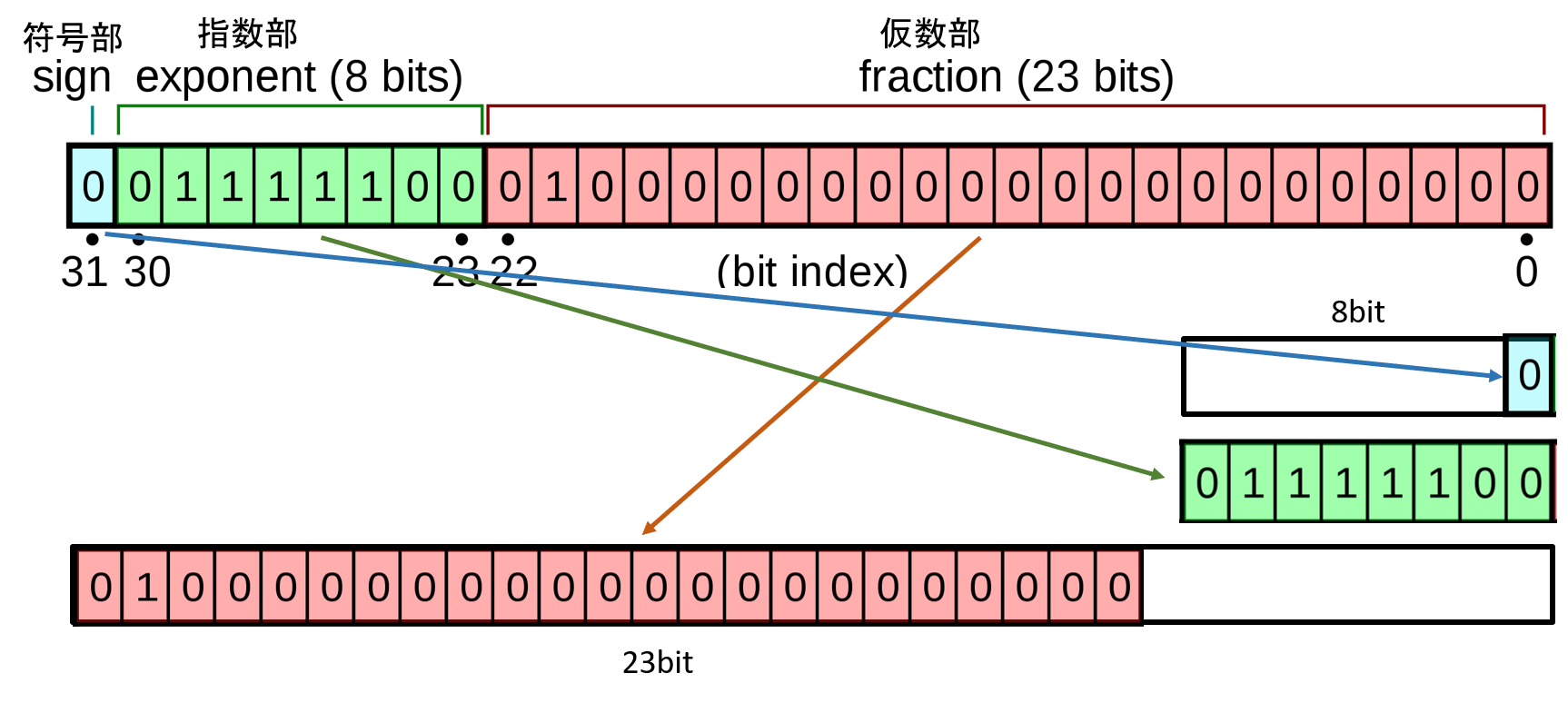
コードにすると以下のstore_ifloat関数のようになります。bitシフトして取り出します。
struct s_ifloat store_ifloat(float num)
{
struct s_ifloat ifloat;
uint32_t mem;
memcpy(&mem, &num, sizeof(uint32_t));
ifloat.sign = mem >> 31;
ifloat.exp = mem >> 23;
ifloat.frac = mem << 9;
return (ifloat);
}
float型ままbit演算しようとするとコンパイラにおこられるので、32bitの符号なし整数型にmemcpyを使ってコピーします。(余談ですが、42tokyoではmemcpyを使うことは禁止されています。自作しなくてはいけません。)
2. 2進数を10進数に変換する
取り出した仮数、指数は2進数は10進数に直して出力しなくてはいけません。ここが一番めんどくさいポイントです。
float型の最大桁数
最初のめんどくさいポイントは桁数です。まず、最大値の桁数から考えてみましょう。
ケチ表現を含む24bitの最大値は、2進数で111,111,111,111,111,111,111,111です。指数部の最大値は前述の通り127ですので、float型の最大値は次のようになります。
float_{max}=1.11111111111111111111111_{(2)}×2^{127}=3.4028...×10^{38}
というわけで、整数部には最大39ケタの数字が入ります。整数部だけでintやlongでは扱えない桁数になっています。
続いて、小数点以下の桁数をみていきましょう。非正規数の場合、ケチ表現をのぞく23bitの仮数部の最小値は、0.000,000,000,000,000,000,000,01になり、指数部の最小値は-126ですので、float型で表現できる最小値(というより最も0に近い数)は次のようになります。
float_{min}=0.00000000000000000000001_{(2)}×2^{-126}=2^{-126-23}=2^{-149}
これを10進数に直すと、小数点以下149桁になります。これは、下記のように2進数の小数を10進数の変換する際、2で割るごとに1桁ずつ増えていってしまうからです。以下のように2^(-n)は小数点以下n桁になります。
2^0=1
2^{-1}=0.5
2^{-2}=0.25
2^{-3}=0.125
以上より、float型を10進数で全て出力するには、整数部は最大39ケタ、小数部は最大149ケタ必要になります。したがって、64bitのlonglong型でも128bitの整数型でも全然たりません。なので、今回は1桁ずつ配列に格納してやることにします。
構造体ifloatに整数部を格納するintarrayと小数部を格納するfracpartという配列を追加します。(fracpartという変数名が変数fracと被ってしまいますがいい名前が思い浮かばなかった)
# define FLT_FRACSIZE 150 // 10進数での小数部の最大桁数 + 計算用余裕1
# define FLT_INTSIZE 39 // 10進数での整数部の最大桁数
struct s_ifloat
{
uint8_t sign;
uint8_t exp;
uint32_t frac;
int8_t intpart[FLT_INTSIZE]; // 追加 10進数の整数部を保存
int8_t fracpart[FLT_FRACSIZE]; // 追加 10進数の小数部を保存
};
※ マクロFLT_FRACSIZEの+1はこのあと行うfracpartを2で割る処理のときに1ケタ余裕があった方が楽だからであり、深い意味はありません。
(補足) float型の精度について
10進数に変換する過程で、桁数は多く出ますが、float型の精度は見た目の桁数より全然小さいです。精度は仮数部24bitで表現できる幅が最大なので、10進数に直すと、7桁程度となります。(2^24-1 = 16,777,215が最大ってことですね。) 数値計算などに用いる際は気をつけましょう。
10進数への変換
この先は、intpartとfracpartに数字を格納していく作業になります。
整数部の変換と小数部の変換で勝手が違うので、以下のように、convert_ifloat関数を2つの関数に分けてしまいます。
void convert_ifloat(struct s_ifloat *ifloat)
{
convert_intpart(ifloat); // 整数部の出力
convert_fracpart(ifloat); // 小数部の出力
}
整数部の変換
仮数部から整数部のみ取り出す
まず、整数部の変換を行います。ここでのめんどくさいポイントは、仮数部fracの全てが整数部なのか、一部が整数部なのか、全てが整数部でないのかが、指数部expの値で変わることです。
なので、まず、expの値で場合わけして、fracから整数部分frac_intpartを取り出します。
void convert_intpart(struct s_ifloat *ifloat)
{
uint8_t i; // カウンタ(あとで使う)
int offset; // fracの整数部分までのoffset
uint32_t intpart_bin; // fracの整数部分を格納
int8_t n[FLT_INTSIZE]; // 2^n乗を格納(あとで使う)
memset(ifloat->intpart, 0, sizeof(ifloat->intpart));
if (ifloat->exp < 127 || ifloat->exp == 255) // 整数部は0
return ;
else if (ifloat->exp < 127 + 23) // ifloat->fracの一部が整数部
offset = ifloat->exp - 127;
else // ifloat->exp >= 127 + 23 => ifloat->fracの全てが整数部
offset = 23;
if (offset == 0)
intpart_bin = 1 << offset;
else
intpart_bin = (ifloat->frac >> (32 - offset)) | (1 << offset);
(後略)
}
expが127より小さい場合は127のバイアスをのぞくと指数部が負になるので、整数部が0になります。また、127+23より大きい場合はfracの23bit全てが整数部になります。それ以外の場合は、一部が整数部となるので、その分をoffsetに保存しています。
なお、intpartはmemsetで最初に0で初期化しておきます。(また、余談ですが、42tokyoではmemsetを使うことも禁止されています。これも自作しなくてはいけません。というかシステムコール以外ほとんど自作します笑)。
そして整数部が0の場合はそのまま返してしまいます。
そして、fracを32-offset分右にシフトすることで、整数部分のみ取り出し、かつその1つ上位にケチ表現分のビットを立てます。これをintpart_binに保存すれば、intpart_binにfracの整数部分のみが入ります。
(修正)20.12.20
offset=0の際に32bitシフトの未定義動作が発生してしまっていたため、修正しました。
整数部を10進数に変換する
あとは普通に基数変換をします。最下位ビットから順にnビット目が立っていたら、intpartに2^(n-1)を足していく作業です。この際、intpartは配列ですので、そのためにarray_double、array_add関数を用意しておきましょう。また、2^nを計算して格納するために、nというintpartと同じ要素数の配列も用意します。
void convert_intpart(struct s_ifloat *ifloat)
{
(さっきの続き)
intpart_bin = (ifloat->frac >> (32 - offset)) | (1 << offset);
memset(n, 0, sizeof(n));
n[FLT_INTSIZE - 1] = 1; // n=1からスタート(最も右を1の位とする)
for (i = 0; i < 24; i++) // 0~24ビットを確認する
{
if (intpart_bin & (1 << i)) // bitが立っていれば2^n乗を足す
array_add(ifloat->intpart, n, FLT_INTSIZE);
array_double(n, FLT_INTSIZE); // nを2倍して次へ
}
while (i++ <= ifloat->exp - 127) // iがexpより小さければその分2倍していく
array_double(ifloat->intpart, FLT_INTSIZE);
24bit分intpart_binをチェックして、bitが立っていればintpartに2^iを足していきます。24bit確認しながら足したら、あとは残りのexpの分intpart自体を2倍していけば、整数部は完成です。
小数部の変換
こちらもだいたい10進数と同じ要領ですが、若干勝手が違います。
仮数部から小数部のみ取り出す
先ほどと同様に小数部のみ取り出しますが、小数部は上の位から確認していくので、最上位ビットからつめてfracpart_binに格納します。
void convert_fracpart(struct s_ifloat *ifloat)
{
int8_t i; // カウンタ
uint32_t fracpart_bin; // fracの整数部分を格納
int8_t n[FLT_FRACSIZE]; // 2^(i-1)を格納
memset(ifloat->fracpart, 0, sizeof(ifloat->fracpart));
if (ifloat->exp >= 23 + 127 || (ifloat->exp == 0 && ifloat->frac == 0)) // 小数部0の場合
return ;
else if (ifloat->exp >= 127) // 一部のみ小数部の場合
fracpart_bin = ifloat->frac << (ifloat->exp - 127);
else if (ifloat->exp == 0) // 非正規数(ケチ表現分bitなし)
fracpart_bin = ifloat->frac;
else // 全て小数部かつ正規数(ケチ表現分bitを入れる)
fracpart_bin = ifloat->frac >> 1 | (1 << 31);
(続く)
}
整数部と同様にmemsetを使って全てのメモリを0初期化し、小数部0の場合はそのままリターンしています。また、正規数の場合はケチ表現分のbitを追加しています。
小数部を10進数に変換
ここまできたら、小数部の10進数に変換していきます。基本的にはfracpart_binのチェックしていき2^(-i-1)の小数部をfracpartに足していくだけです。
整数部と同様に2^(-i-1)を格納するための配列nを用意してそれを足します。今回は倍じゃなくて2で割るので、そのための関数array_divbytwoを用意しておきます。
void convert_fracpart(struct s_ifloat *ifloat)
{
(さっきの続き)
memset(n, 0, sizeof(n));
n[0] = 5; // 2^(-1)(=0.5)からスタート
for (i = 0; i < (126 - ifloat->exp); i++)
array_divbytwo(n, FLT_FRACSIZE); // あらかじめ指数に合わせて割っておく
for (i = 0; i < 24; i++)
{
if (fracpart_bin & (1 << (31 - i))) // bitが立っていればfracpartに足していく
array_add(ifloat->fracpart, n, FLT_FRACSIZE);
array_divbytwo(n, FLT_FRACSIZE);
}
気をつけなければいけないのはfracpartにnを足していく前に、126-exp回nを2で割らないといけません。これで、fracpart_binの位置を指数に合わせることができます。
そのあとは24bit分fracpart_binを確認し、bitが立っていればfracpartにnを足していきます。
これで、小数部の変換も終了です。
3. 出力
10進数への変換が終わったので、あとは出力するだけです。今回は丸めについては扱わないので、単純に変換後の数を全て表示するようにします(見にくいですが)
printfに実装する場合は%f, %g, %eなどの仕様に従いうまく表示させましょう。(実はここも結構しんどかったです)
void print_ifloat(struct s_ifloat ifloat)
{
int i;
char c;
if (ifloat.exp == 255 && ifloat.frac != 0) // nanの場合
{
write(1, "nan\n", 4);
return ;
}
if (ifloat.sign == 1) // 符号ビットが1の場合'-'を出力
write(1, "-", 1);
if (ifloat.exp == 255) // infの場合
{
write(1, "inf\n", 4);
return ;
}
for (i = 0; i < FLT_INTSIZE; i++) // 整数部の出力
{
c = ifloat.intpart[i] + '0';
write(1, &c, 1);
}
write(1, ".", 1);
for (i = 0; i < FLT_FRACSIZE - 1; i++) // 小数部の出力
{
c = ifloat.fracpart[i] + '0';
write(1, &c, 1);
}
}
これで、終了です。
結果
比較用の関数を作って、結果を見てみましょう。
// 比較表示用関数
void printcomp(float num)
{
// printfの表示(nan, inf以外は整数部39ケタ、小数部149ケタ表示する)
if (isnan(num) || isinf(num))
printf("printf : %f\n", num);
else
printf("printf : %0*.*f\n", FLT_INTSIZE + FLT_FRACSIZE, FLT_FRACSIZE - 1, num);
// 自作printfloatの表示(nan, inf以外は整数部39ケタ、小数部149ケタ表示する)
fflush(stdout);
write(1, "putfloat: ", 10);
printfloat(num);
write(1, "\n", 1);
}
int main(void)
{
float num;
uint32_t mem;
printcomp(42);
printcomp(4.2);
printcomp(M_PI); // 円周率 (math.hで定義)
printcomp(FLT_MAX); // 正規数の最大 = 3.40282347e+38F (float.hで定義)
printcomp(FLT_MIN); // 正規数の最小= 1.17549435e-38F (float.hで定義)
mem = 1;
memcpy(&num, &mem, sizeof(uint32_t));
printcomp(num); // 非正規数の最小 (仮数部の最下位bitのみ1)
printcomp(0.0/0.0); // nan
printcomp(1.0/0.0); // inf
printcomp(-1.0/0.0); // -inf
return (0);
}
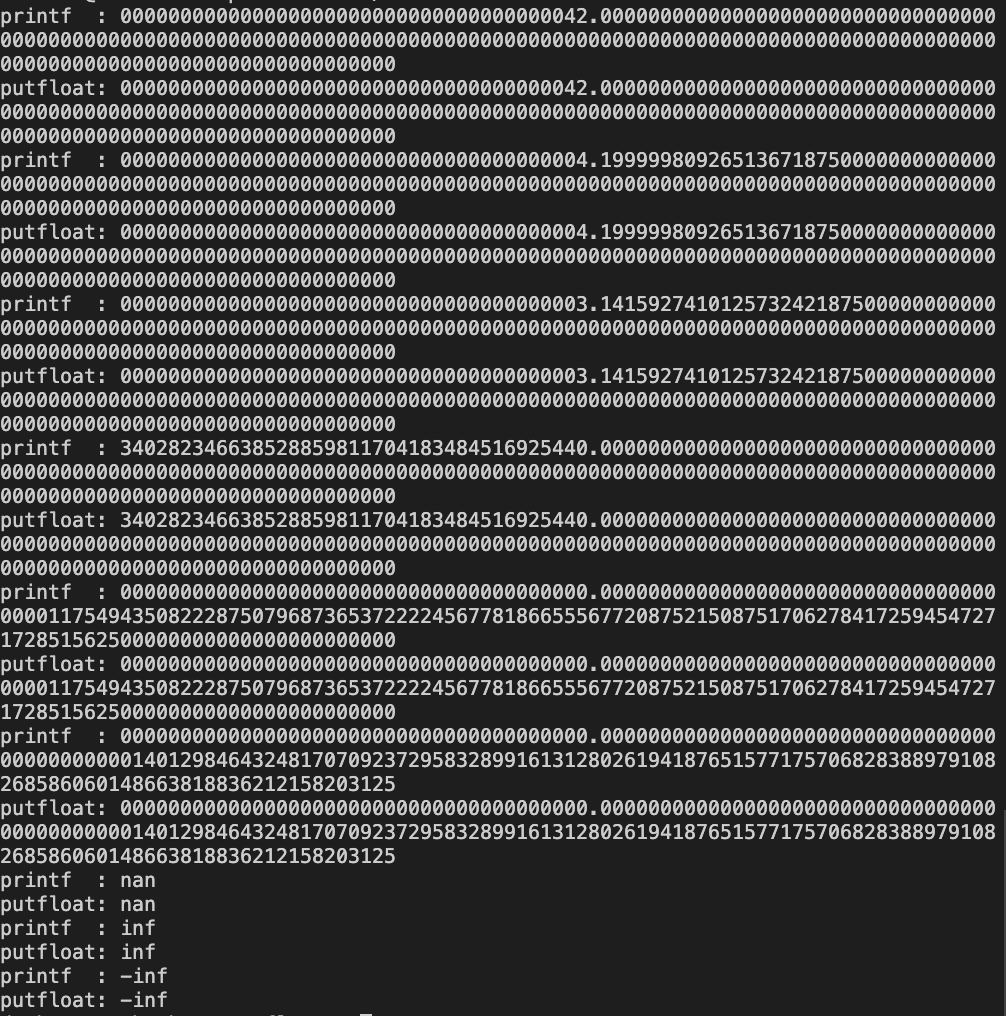
出力結果。
printf : 000000000000000000000000000000000000042.00000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000
putfloat: 000000000000000000000000000000000000042.00000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000
printf : 000000000000000000000000000000000000004.19999980926513671875000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000
putfloat: 000000000000000000000000000000000000004.19999980926513671875000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000
printf : 000000000000000000000000000000000000000.00000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000
putfloat: 000000000000000000000000000000000000000.00000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000
printf : 000000000000000000000000000000000000003.14159274101257324218750000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000
putfloat: 000000000000000000000000000000000000003.14159274101257324218750000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000
printf : 340282346638528859811704183484516925440.00000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000
putfloat: 340282346638528859811704183484516925440.00000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000
printf : 000000000000000000000000000000000000000.00000000000000000000000000000000000001175494350822287507968736537222245677818665556772087521508751706278417259454727172851562500000000000000000000000
putfloat: 000000000000000000000000000000000000000.00000000000000000000000000000000000001175494350822287507968736537222245677818665556772087521508751706278417259454727172851562500000000000000000000000
printf : 000000000000000000000000000000000000000.00000000000000000000000000000000000000000000140129846432481707092372958328991613128026194187651577175706828388979108268586060148663818836212158203125
putfloat: 000000000000000000000000000000000000000.00000000000000000000000000000000000000000000140129846432481707092372958328991613128026194187651577175706828388979108268586060148663818836212158203125
printf : nan
putfloat: nan
printf : inf
putfloat: inf
printf : -inf
putfloat: -inf
コピペしたのかと思うほどきれいにそろってますね。最初にうまくいったときは結構興奮しました。(これが楽しくてコーディングがやめられません)
終わりに
こんなこと知らなくても実務上問題になることはほぼないのだろうと思います。ですが、このために浮動小数点のことしか考えなかった数日間で私のエンジニアとしての基礎体力は相当上がったと思います。(もともとnot ITなエンジニアで、bit演算ってなんですか。って状態からのスタートでした。)
こういうコンピュータサイエンスの基礎体力から身に付けられるのが42のカリキュラムです。本当に楽しいので、皆さんも是非42Tokyoへの入学を検討してみてはいかがでしょうか。
明日の42tokyo Advent Calendar 2020は、Hinataさんです。何やら中国コスメの話があるらしいですが...多分僕にはよくわからないです!! なんだかキラキラですね!!!!! お楽しみに!!