こんにちは、@daifukusanです。
今回は、pythonから使える数理最適化のライブラリであるpulpから呼び出せる便利な関数を自作した話になります。
この関数は、有償のソルバー(Gurobiなど)が標準で提供しているもののため、実務においてはそちらを使ったほうが安全かつ高速です。
趣味で最適化ソルバーを利用したい場合に、参考になれば幸いです。
今回作成した関数は、computeIISという関数で既約不整合部分系(Irreducible Inconsistent Subsystem: IIS) と呼ばれる制約条件の一部を出力するものになります。
この言葉を知らない方もいるかと思うので、まずはそちらから説明します。
実装だけ知りたい方は、3章、4章のみ見てください
1. 既約不整合部分系(IIS)とは
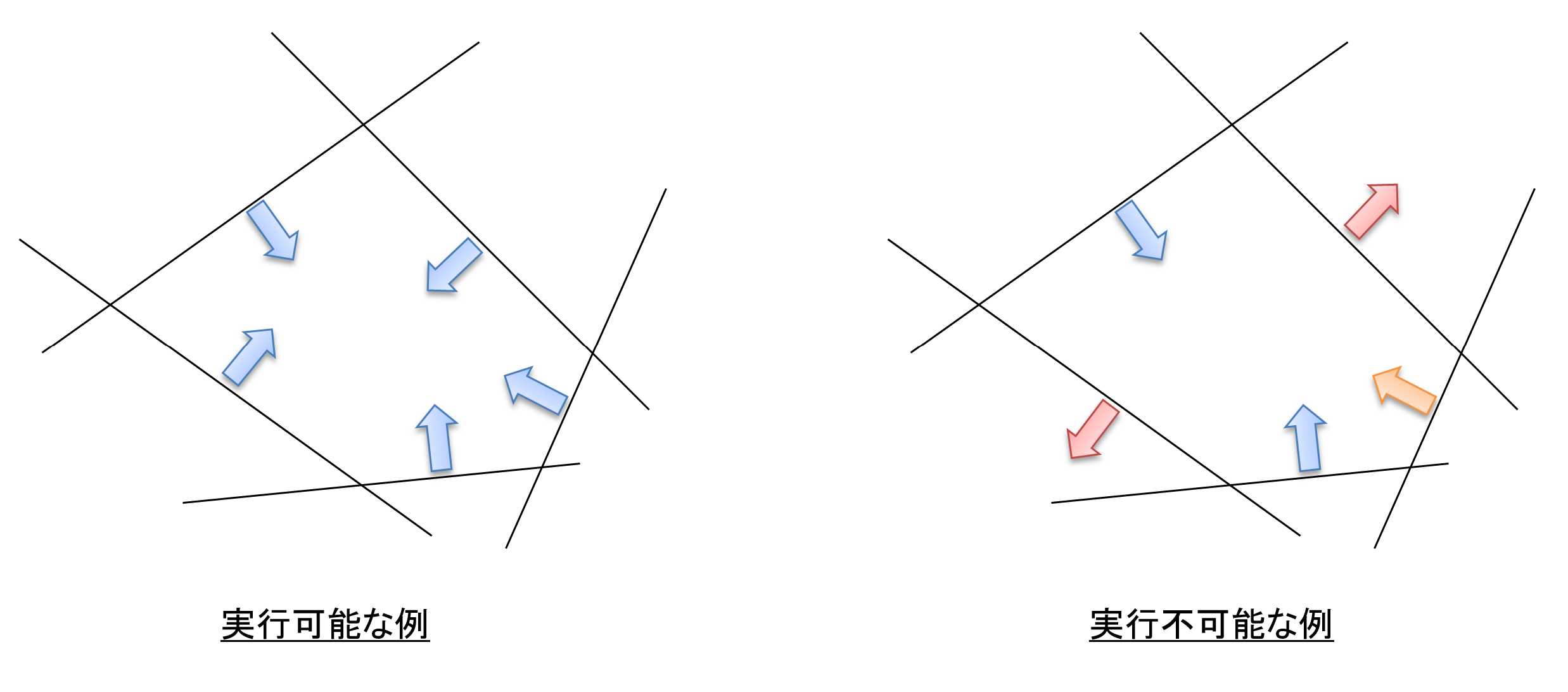
既約不整合部分系を説明するため、数理モデルの「実行可能」と「実行不可能」の状態を図で示します。
図中の直線は制約条件の境界を表します。例えば、$5x + 3y \leq 8$ という不等式では、等号が成立する部分がこの境界です。矢印は不等号が成立する領域を示し、境界で分けられた領域のうち矢印側が制約条件を満たす領域です。
左図では、5つの制約条件すべてを満たす領域が中心に存在します。この領域を「実行可能領域」と呼び、実行可能領域がある場合、数理モデルは実行可能(feasible) と言えます。
右図では、赤色の矢印が互いに反対を向いています。この場合、5つの制約条件をすべて満たす領域は存在しません(赤色の領域が画面外で交わっても、オレンジ色の矢印の条件を満たせません)。実行可能領域がない数理モデルを実行不可能(infeasible) と言います。
既約不整合部分系とは、実行不可能な数理モデルにおいて、「実行不可能の原因となる最小の制約条件集合」を指します。右図では、赤色とオレンジ色の矢印の3つの制約条件が同時に満たせないため、これらが既約不整合部分系(IIS)となります。
簡単に言えば、IISは「制約条件間の矛盾を引き起こす核となる部分」です。
図的に解釈しやすかったため、不等式制約を用いて説明しました。
ただし、既約不整合部分の概念自体は等式制約・不等式制約に関わらず定義できるものであるため、注意して下さい。
2. 既約不整合部分系(IIS)の用途
IISの主な用途は以下の3つです。
- 数理モデルのデバッグ
- 運用時のオペレーションミスのチェック
- 説明可能なAI
2.1. 数理モデルのデバッグ
設計の誤りやコーディングミスによって作成された誤った数理モデルの修正指針を得られます。例えば、実行可能なはずのテストデータで実行不可能となった場合、IISが示す制約条件の周辺にバグがある可能性が高く、効率的なデバッグが可能になります。
2.2. 運用時のオペレーションミスのチェック
システム稼働後の実運用で効果を発揮します。業務担当者がパラメータ入力時に起こした、単純な入力チェックでは検出困難なミスを防げます。IISに含まれる制約条件には入力ミスしたパラメータに関わる制約が含まれる可能性が高いため、原因の特定が容易になります(ただし、原因の正確な類推には業務制約の理解が必要です)。
2.3. 説明可能なAI
業務担当者が正しいパラメータで実行したにもかかわらず実行不可能となった場合、業務が成立しない条件を与えたことになります。この状況では業務成立のために関係部署との調整(納期延長や原材料追加発注など)が必要ですが、単に「システムが実行不可能と出力した」という理由だけでは調整は難しいでしょう。ほとんどの場合、業務が成立しない具体的理由を説明する必要があります。このような場合、IISは業務不成立の根拠を示す有効な手段となります。
これらの有用性があるIISですが、pulpの標準ソルバーCBCには実装されていないため、有償ソルバーのない環境では利用できません。そこで今回、IISを計算するcomputeIIS関数を自作しました。
3. IISの計算処理
IISの計算方法については、以下の資料が参考になります。
これらによると、IISを計算する方法は主に以下の4つです。
- Deletion Filterによる方法
- Additive Methodによる方法
- 1と2の組合せ
- Elastic Filterによる方法
今回はDeletion Filterを採用しました。Elastic Filterは実装が最も容易ですが、変数が制約条件数分増加するため大規模問題には不向きと判断しました。
論文によると、IISの対象となる制約条件は3種類あります。
- LC:一次の等式(不等式)で表される制約条件
- BD:各変数の上限・下限条件
- IR:変数の整数制約
本来はすべての制約条件でIISを計算すべきですが、今回はLCのみを対象とします。これは実装の簡略化と、BD・IR制約は実務上取り除くことが現実的でないためです。
3.1. Deletion Filterの仕組み
Deletion Filterの処理の流れは以下の通りです。
FUNCTION FindIIS(constraintSet)
// Input: constraintSet - 実行不可能な制約の集合
// 各制約について順に処理する
FOR EACH constraint IN constraintSet DO
// 現在の制約を一時的に除外
tempSet = constraintSet - {constraint}
// 制約を除いた集合の実行可能性をチェック
IF IsFeaisble(tempSet) THEN
// 実行可能になった場合は、その制約は必要なので戻す
constraintSet = constraintSet // 変更なし(制約を維持)
ELSE
// 実行不可能のままの場合は、その制約は冗長なので削除
constraintSet = tempSet // 制約を永久に削除
END IF
END FOR
// Output: 単一のIIS(Irreducible Infeasible Subset)を構成する制約の集合
RETURN constraintSet
END FUNCTION
Deletion Filterでは、実行不可能な数理モデルから制約条件を1つずつ除去します。除去後も実行不可能なら、その制約は実行可能性に影響しないため削除します。実行可能になれば、その制約が実行不可能性に寄与しているため元に戻します。最終的に残った制約集合がIISとなります。
処理の詳細は以下のスライドが参考になります。
https://www.sce.carleton.ca/faculty/chinneck/docs/CPAIOR07InfeasibilityTutorial.pdf#page=8
このロジックをそのまま実装すると、制約条件の数だけ数理モデルを解く必要があり、大規模問題では計算時間が膨大になります。そこで以下の2つの工夫を加えました。
3.2. Deletion処理のグループ化
制約条件を1つずつではなく、まとめて除去します。除去後も実行不可能なら一括削除し、実行可能なら元に戻します。この処理を制約条件数が十分減少するか、これ以上除去できなくなるまで繰り返します。本実装では制約条件を10分割し、分割単位で処理することで大幅な高速化を実現しています。
3.3. 最適化処理の打ち切り
グループ化処理では正確な実行可能性判断が不要なため、最適化処理を一定時間で打ち切ります。処理が進むにつれ制約条件数が減少し問題規模が小さくなるため、後半ほど解法速度は向上します。そのため序盤で時間切れとなる問題を後回しにしても全体効率への影響は限定的です。
3.4. computeIISのソースコード
以下が、今回作成したcomputeIISと内部で呼び出されるサブルーチンのソースコードです。
rebuild_model_with_active_variablesという関数は、制約を除去した際にどこからも参照されない変数がある場合のエラーを回避するため、不要な変数を除去したモデルを再構築する関数です。
import pulp
# 制約を削除した後に、使われている変数だけを含む新しいモデルを作成する関数
def rebuild_model_with_active_variables(old_model):
# 新しいモデルを作成
new_model = pulp.LpProblem(old_model.name, old_model.sense)
# 目的関数を移行
if old_model.objective:
new_model.objective = old_model.objective
# 使用中の変数を特定するための集合
active_vars = set()
# 制約条件から使用されている変数を収集
for constraint_name, constraint in old_model.constraints.items():
# 各制約式での変数を収集
for var in constraint.keys():
active_vars.add(var)
# 制約を新しいモデルに追加
new_model += constraint, constraint_name
# 目的関数に使われている変数も収集
for var in old_model.objective.keys():
active_vars.add(var)
return new_model
# Deletion処理をグループ化して行う関数
def deletion_filter_group(base_prob, prob, k_div, verbose=False):
cons_keys = list(prob.constraints.keys())
n_cons = len(prob.constraints)
for i in range(k_div):
if verbose:
print(f"Remove {i}th Group Constraint ({int((i/k_div)*n_cons)}-{int(((i+1)/k_div)*n_cons)}): ", end="")
cons_group = cons_keys[int((i/k_div)*n_cons):int(((i+1)/k_div)*n_cons)]
for name in cons_group:
del prob.constraints[name]
try:
status = prob.solve(pulp.PULP_CBC_CMD(msg=False, logPath='cbc_log.txt', timeLimit=15.0))
except:
# 未参照の変数がある場合、エラーが発生するため、不要な変数を除去したモデルを再構築
prob = rebuild_model_with_active_variables(prob)
status = prob.solve(pulp.PULP_CBC_CMD(msg=False, logPath='cbc_log.txt', timeLimit=15.0))
if status == pulp.LpStatusOptimal or status == pulp.LpStatusNotSolved:
if verbose:
print(f"{pulp.LpStatus[status]} -> retained")
for name in cons_group:
prob.addConstraint(name=name, constraint=base_prob.constraints[name])
else:
if verbose:
print(f"{pulp.LpStatus[status]} -> deleted")
return prob
def deletion_filter(base_prob, prob, verbose=False):
iis_list = []
cons_keys = list(prob.constraints.keys())
for name in cons_keys:
if verbose:
print(f"Remove Constraint {name} : ", end="")
del prob.constraints[name]
try:
status = prob.solve(pulp.PULP_CBC_CMD(msg=False, logPath='cbc_log.txt', timeLimit=60.0))
except:
# 未参照の変数がある場合、エラーが発生するため、不要な変数を除去したモデルを再構築
prob = rebuild_model_with_active_variables(prob)
status = prob.solve(pulp.PULP_CBC_CMD(msg=False, logPath='cbc_log.txt', timeLimit=60.0))
if status == pulp.LpStatusOptimal or status == pulp.LpStatusNotSolved:
if verbose:
print(f"{pulp.LpStatus[status]} -> retained")
prob.addConstraint(name=name, constraint=base_prob.constraints[name])
iis_list.append(name)
else:
if verbose:
print(f"{pulp.LpStatus[status]} -> deleted")
return iis_list
def computeIIS(base_prob: pulp.LpProblem, verbose=False):
prob = base_prob.deepcopy()
epoch = 0
prev_n_cons = -1
n_cons = len(prob.constraints)
k_div = 15
#
while n_cons > k_div*2 and prev_n_cons != n_cons:
prob = deletion_filter_group(base_prob, prob, k_div, verbose)
prev_n_cons = n_cons
n_cons = len(prob.constraints)
if verbose:
print(f'epoch finished. rest constraints:{n_cons}')
epoch += 1
return deletion_filter(base_prob, prob, verbose)
4. computeIISの実行例
実際に、computeIISを使って、どのようなことが分かるのか見てみます。
検証に使う最適化モデルとして、数独を解く数理モデルを用意しました。
import pulp
def solve_sudoku(fixed):
# 数理最適化問題(最大化)を宣言
problem = pulp.LpProblem("数独", pulp.LpMinimize)
# 集合を定義
I = list(range(9))
J = list(range(9))
K = list(range(1,10))
B = list(range(9))
Block = []
for b in B:
M = b // 3
N = b % 3
tmp = []
for i in range(3):
for j in range(3):
tmp.append((3*M+i,3*N+j))
Block.append(tmp)
# 変数を宣言
# x[i,j,k] : マス(i,j)に数字kを入れるとき1, そうでなければ0
x = {}
for i in I:
for j in J:
for k in K:
x[i,j,k] = pulp.LpVariable(f"x({i},{j},{k})", cat=pulp.LpBinary)
##### 制約条件を宣言 #####
# 1. 各マスには、1~9までの値が1つ入る
for i in I:
for j in J:
problem += pulp.lpSum(x[i,j,k] for k in K) == 1, f"マス({i},{j})に関する制約"
# 2.1. すべての横列には、1~9までの数字が1回ずつ入る。
for i in I:
for k in K:
problem += pulp.lpSum(x[i,j,k] for j in J) == 1, f"行{i},数字{k}に関する制約"
# 2.2. すべての縦列には、1~9までの数字が1回ずつ入る。
for j in J:
for k in K:
problem += pulp.lpSum(x[i,j,k] for i in I) == 1, f"列{j},数字{k}に関する制約"
# 3. 各ブロックには、1~9までの数字が1回ずつ入る。
for b in B:
for k in K:
problem += pulp.lpSum(x[i,j,k] for i,j in Block[b]) == 1, f"ブロック{b},数字{k}に関する制約"
# 4. 最初から値が入っているマスの値は固定する。
for i,j,k in fixed:
problem += x[i,j,k] == 1, f'マス({i},{j})を数字{k}で固定する制約'
##### 目的関数を宣言 #####
problem += 0, "目的なし"
##### 最適化問題を解く ####
result_status = problem.solve()
solved_puzzle = [[0 for _ in J] for _ in I]
if result_status == pulp.LpStatusOptimal:
# 最適解が得られていたら解を取得する
for i in I:
for j in J:
for k in K:
if x[i,j,k].value() == 1.0:
solved_puzzle[i][j] = k
return result_status, solved_puzzle, problem
puzzle, fixed = read_input('data/sudoku01_bad.csv')
status, solved_puzzle, problem = solve_sudoku(fixed)
IISを活用する際は、制約条件に適切な名前をつけることが重要です。分かりやすい名前により、得られたIISの解釈と活用が容易になります。
以下の数独データを例に考えてみましょう:
# 数独データ
+-------+-------+-------+
| 7 2 | | |
| 4 9 | 5 3 7 | 8 2 |
| 5 | 1 | |
+-------+-------+-------+
| 1 | 2 | 5 6 3 |
| 3 5 | 6 8 | 1 9 |
| 9 7 6 | | 4 2 |
+-------+-------+-------+
| 6 7 | 2 4 1 | 8 3 |
| 5 | 9 7 8 | 4 |
| 6 8 | 3 6 5 | 9 1 |
+-------+-------+-------+
左下のブロックに注目すると、6が書かれたマスが2つあり、数独として成立していません。この問題を数理モデルで解こうとすると、Infeasible(実行不可能)と判定されます。
このデータにcomputeIISを実行した結果は以下の通りです(実行結果は下4行で、それより上は実行時のログです。引数verboseをFalseにするとログは非表示になります)
compute IIS start. rest constraints:370
Remove 0th Group Constraint (0-37): Infeasible -> deleted
Remove 1th Group Constraint (37-74): Infeasible -> deleted
Remove 2th Group Constraint (74-111): Infeasible -> deleted
Remove 3th Group Constraint (111-148): Infeasible -> deleted
Remove 4th Group Constraint (148-185): Infeasible -> deleted
Remove 5th Group Constraint (185-222): Infeasible -> deleted
Remove 6th Group Constraint (222-259): Infeasible -> deleted
Remove 7th Group Constraint (259-296): Infeasible -> deleted
Remove 8th Group Constraint (296-333): Optimal -> retained
Remove 9th Group Constraint (333-370): Optimal -> retained
epoch finished. rest constraints:74
Remove 0th Group Constraint (0-7): Optimal -> retained
Remove 1th Group Constraint (7-14): Infeasible -> deleted
Remove 2th Group Constraint (14-22): Infeasible -> deleted
Remove 3th Group Constraint (22-29): Infeasible -> deleted
Remove 4th Group Constraint (29-37): Infeasible -> deleted
Remove 5th Group Constraint (37-44): Infeasible -> deleted
Remove 6th Group Constraint (44-51): Infeasible -> deleted
Remove 7th Group Constraint (51-59): Optimal -> retained
Remove 8th Group Constraint (59-66): Infeasible -> deleted
Remove 9th Group Constraint (66-74): Optimal -> retained
epoch finished. rest constraints:23
Remove 0th Group Constraint (0-2): Infeasible -> deleted
Remove 1th Group Constraint (2-4): Infeasible -> deleted
Remove 2th Group Constraint (4-6): Infeasible -> deleted
Remove 3th Group Constraint (6-9): Optimal -> retained
Remove 4th Group Constraint (9-11): Infeasible -> deleted
Remove 5th Group Constraint (11-13): Optimal -> retained
Remove 6th Group Constraint (13-16): Infeasible -> deleted
Remove 7th Group Constraint (16-18): Optimal -> retained
Remove 8th Group Constraint (18-20): Infeasible -> deleted
Remove 9th Group Constraint (20-23): Infeasible -> deleted
epoch finished. rest constraints:7
Remove Constraint ブロック6,数字6に関する制約 : Optimal -> retained
Remove Constraint マス(5,1)を数字7で固定する制約 : Infeasible -> deleted
Remove Constraint マス(5,2)を数字6で固定する制約 : Infeasible -> deleted
Remove Constraint マス(6,0)を数字6で固定する制約 : Optimal -> retained
Remove Constraint マス(6,2)を数字7で固定する制約 : Infeasible -> deleted
Remove Constraint マス(8,0)を数字6で固定する制約 : Optimal -> retained
Remove Constraint マス(8,1)を数字8で固定する制約 : Infeasible -> deleted
### show IIS result ###
0 ブロック6,数字6に関する制約
1 マス(6,0)を数字6で固定する制約
2 マス(8,0)を数字6で固定する制約
ログを見ると、最初は370本あった制約条件がグループ化したDeletion処理によって74本に削減され、次の繰り返しで7本にまで減少しています。この段階で個別処理に切り替えることで、効率的に計算を完了させています。
最終的に得られたIISは3つの制約条件で構成されています:
- ブロック6(左下ブロック)の数字6に関する制約
- マス(6,0)を数字6で固定する制約
- マス(8,0)を数字6で固定する制約
これらの制約条件から、左下ブロック内の2つの位置に数字6が重複して配置されていることが問題の原因だと容易に特定できます。
5. まとめ
本稿では、数理モデルの構築・運用時に強力なツールとなるIISを求める処理を自作しました。有償ソルバーを使用できる環境であれば、処理速度と安全性の観点からそちらの利用をお勧めします。
しかし、個人で最適化を勉強している方にとって有償ソルバーは敷居が高いため、同様の課題に直面している方はぜひ今回の手法を参考にしてみてください。