こんにちは、@daifukusanです。
自身の備忘録も兼ねて、線形計画問題の双対問題の導出手順を整理します。
ORや数理最適化を専門にされている方からすると自明なものですが、私と同じように導出が苦手な方の参考になれば幸いです。
1. 導出手順の整理
標準形の線形計画問題とその双対問題は以下の形をしています。
\begin{array}{ccc}
\begin{aligned}
\text{(LP0)} &\\
\min & \quad c^T x \\
\text{s.t.} & \quad Ax = b \\
& \quad x \geq 0
\end{aligned}
&
\hspace{3em}
&
\begin{aligned}
\text{(DP0)} &\\
\max & \quad b^T y \\
\text{s.t.} & \quad A^Ty \leq c \\
\\
\end{aligned}
\end{array}
ここで、線形計画問題が標準形であるとは、以下を満たす線形計画問題を指します。
- 目的関数を最小化する問題である
- すべての制約条件が等式制約である
- 変数 $x$ は非負である
一般の線形計画問題は、素直に表現した場合にこの標準形の形になるとは限りませんが、様々な変換を行うことで標準形にどんな線形計画問題でも標準形の形に書き換え可能であることが知られています。
そこで、今回は以下の方針で双対問題を導出していきます。
- 線形計画問題を標準形の形に書き換える
- 標準形の線形計画問題に対応する双対問題を得る
- 得られた双対問題を変形し、もとの線形計画問題の形と比較する
2. 行列表記の双対問題の導出
ここからは、様々な形式の線形計画問題に対して双対問題の導出を行い、得られた双対問題の形からその変換の法則性を整理します。
2.1. 目的関数を最大化する問題の場合
まずは、目的関数の最適化方向が最小化ではなく、最大化の場合を見ていきます。
この場合の定式化は以下のとおりです。
\begin{aligned}
\max & \quad c^T x \\
\text{s.t.} & \quad Ax = b \\
& \quad x \geq 0
\end{aligned}
このような問題の場合、$\bar{c} = -c$ と置くことで、$\bar{c}^Tx$ の最小化問題として書き直すことができます。
\begin{aligned}
\min & \quad \bar{c}^T x \\
\text{s.t.} & \quad Ax = b \\
& \quad x \geq 0
\end{aligned}
上記の問題は標準形のため、(LP0)から(DP0)への変換が使えます。
\begin{aligned}
\max & \quad b^T y' \\
\text{s.t.} & \quad A^T y' \leq \bar{c}
\end{aligned}
最後に、$\bar{c} = -c$ であること、$y'$ は自由変数のため$y' = -y$と置き換えても問題ないことを踏まえると、線形計画問題の双対問題は以下のように変換できます。
\begin{array}{ccccc}
\begin{aligned}
\text{(LP1)} &\\
\max & \quad c^T x \\
\text{s.t.} & \quad Ax = b \\
& \quad x \geq 0
\end{aligned}
&
\hspace{1em}
&
\begin{aligned}
\text{(DP1')} &\\
\max & \quad -b^T y \\
\text{s.t.} & \quad -A^Ty \leq -c\\
\\
\end{aligned}
&
\Leftrightarrow
&
\begin{aligned}
\text{(DP1)} &\\
\min & \quad b^T y \\
\text{s.t.} & \quad A^Ty \geq c\\
\\
\end{aligned}
\end{array}
このことから、主問題で最適化方向(最小化 or 最大化)が反転すると双対問題でも最適化方向が反転し、制約条件の不等号の向きも反転することがわかりました。
2.2. 変数が分離可能な場合
次に変数が$x_1$ 、$x_2$ のように分けて書ける場合を見ていきます。
扱うのは、以下の問題です。
\begin{aligned}
\min & \quad c_1^T x_1 + c_2^T x_2 \\
\text{s.t.} & \quad Ax_1 + Bx_2 = b \\
& \quad x_1,x_2 \geq 0
\end{aligned}
この場合、まず $\bar{c},\bar{A},\bar{x}$ を以下のように定義します。
\begin{aligned}
\bar{c} = \begin{bmatrix}
c_1 \\ c_2
\end{bmatrix},\quad
\bar{A} =[A \quad B],\quad
\bar{x} = \begin{bmatrix}
x_1 \\ x_2
\end{bmatrix}
\end{aligned}
これらを使って、標準形の線形計画問題とその双対問題が得られます。
\begin{array}{ccc}
\begin{aligned}
\text{(LP2')} &\\
\min & \quad \bar{c}^T \bar{x} \\
\text{s.t.} & \quad \bar{A}\bar{x} = b \\
& \quad \bar{x} \geq 0
\end{aligned}
&
\hspace{3em}
&
\begin{aligned}
\text{(DP2')} &\\
\max & \quad b^T y \\
\text{s.t.} & \quad \bar{A}^Ty \leq \bar{c}\\
\\
\end{aligned}
\end{array}
$\bar{c},\bar{A},\bar{x}$ を展開することで、最終的に以下の式が得られます。
\begin{array}{ccc}
\begin{aligned}
\text{(LP2)} &\\
\min & \quad c_1^T x_1 + c_2^T x_2 \\
\text{s.t.} & \quad Ax_1 + Bx_2 = b \\
& \quad x_1,x_2 \geq 0
\end{aligned}
&
\hspace{3em}
&
\begin{aligned}
\text{(DP2)} &\\
\max & \quad b^T y \\
\text{s.t.} & \quad A^T y \leq c_1\\
& \quad B^T y \leq c_2\\
\end{aligned}
\end{array}
このことから、主問題において変数が分離可能な場合、双対問題では制約条件が分離されます。 また、その制約条件は、分離した変数に対応する目的関数の係数ベクトル、制約条件の係数行列のみを使って表されています。
これは、線形計画問題の相補性条件を考えると、ある意味当然の結果です。
2.3. 制約条件が分離可能な場合
変数と同様に、制約条件が分離可能な場合も見ていきましょう。
\begin{aligned}
\min & \quad c^T x \\
\text{s.t.} & \quad Ax = b_1 \\
& \quad Bx = b_2 \\
& \quad x \geq 0
\end{aligned}
定式化に必要な定数 $\bar{b}、\bar{A}$ を次のように定義します。
\begin{aligned}
\bar{b} = \begin{bmatrix}
b_1 \\ b_2
\end{bmatrix},\quad
\bar{A} =\begin{bmatrix}
A \\ B
\end{bmatrix}
\end{aligned}
これらの定数を使えば、標準形の線形計画問題とその双対問題が得られます。
\begin{array}{ccc}
\begin{aligned}
\text{(LP3')} &\\
\min & \quad c^T x \\
\text{s.t.} & \quad \bar{A} x = \bar{b} \\
& \quad x \geq 0
\end{aligned}
&
\hspace{3em}
&
\begin{aligned}
\text{(DP3')} &\\
\max & \quad \bar{b}^T y \\
\text{s.t.} & \quad \bar{A}^Ty \leq c\\
\\
\end{aligned}
\end{array}
最後に$\bar{b}、\bar{A}$を展開しますが、それに合わせて変数$y$も$y_1, y_2$に分離します。
\begin{array}{ccc}
\begin{aligned}
\text{(LP3)} &\\
\min & \quad c^T x \\
\text{s.t.} & \quad Ax = b_1 \\
& \quad Bx = b_2 \\
& \quad x \geq 0 \\
\end{aligned}
&
\hspace{3em}
&
\begin{aligned}
\text{(DP3)} &\\
\max & \quad b_1^T y_1 + b_2^T y_2 \\
\text{s.t.} & \quad A^T y_1 + B^T y_2 \leq c\\
\\
\\
\end{aligned}
\end{array}
以上のことから分かる通り、主問題において制約条件が分離可能な場合、双対問題では変数が分離されます。 また、目的関数の係数ベクトルは、分離した制約条件に対応する右辺のベクトルで表されます。2.2の結果と比較すると、主問題と双対問題の形がちょうど逆転していることが分かる思います。
現実の問題では、変数、制約条件のどちらも分離可能なケースをよく扱います。
このような問題についても、2.2.と2.3.を組み合わせることで、同じように導出が可能です。
ここではその導出はせず、結果のみ記します。
\begin{array}{ccc}
\begin{aligned}
\text{(LP2+3)} &\\
\min & \quad c_1^T x + c_2^T x \\
\text{s.t.} & \quad Ax_1 + B x_2 = b_1 \\
& \quad C x_1 + D x_2 = b_2 \\
& \quad x_1, x_2 \geq 0 \\
\end{aligned}
&
\hspace{3em}
&
\begin{aligned}
\text{(DP2+3)} &\\
\max & \quad b_1^T y_1 + b_2^T y_2 \\
\text{s.t.} & \quad A^T y_1 + C^T y_2 \leq c_1\\
& \quad B^T y_1 + D^T y_2 \leq c_2\\
\\
\end{aligned}
\end{array}
2.4. 制約条件が不等式制約の場合
制約条件が不等式であるケースも現実の問題では頻出します。
この場合、補助変数 $w$を使い、以下の等価な問題として定義します。
\begin{array}{ccc}
\begin{aligned}
\min & \quad c^T x \\
\text{s.t.} & \quad Ax \geq b \\
& \quad x \geq 0
\end{aligned}
&
\Leftrightarrow
&
\begin{aligned}
\min & \quad c^T x + 0 w \\
\text{s.t.} & \quad Ax - Iw = b \\
& \quad x \geq 0, w \geq 0
\end{aligned}
\end{array}
ここで $I$ は単位行列です。
この定式化は変数が$x$と$w$に分離された線形計画問題のため、(LP2)から(DP2)の導出が使えます。
\begin{array}{ccccc}
\begin{aligned}
\text{(LP4)} &\\
\min & \quad c^T x + 0 w \\
\text{s.t.} & \quad Ax - Iw = b \\
& \quad x \geq 0, w \geq 0
\end{aligned}
&
\hspace{1em}
&
\begin{aligned}
\text{(DP4')} &\\
\max & \quad b^T y \\
\text{s.t.} & \quad A^T y \leq c\\
& \quad - I y \leq 0\\
\end{aligned}
&
\Leftrightarrow
&
\begin{aligned}
\text{(DP4)} &\\
\max & \quad b^T y \\
\text{s.t.} & \quad A^T y \leq c\\
& \quad y \geq 0\\
\end{aligned}
\end{array}
以上の結果から、不等式制約をもつ線形計画問題の場合、双対問題ではその制約式に対応する変数に下限(上限)制約が追加されることが分かります。
不等号の向きについては、この記事の最後に整理したいと思います。
2.5. 変数が自由変数(非負条件なし)の場合
標準形の問題では変数$x$ は非負でしたが、この条件がない場合を考えてみます。
このような場合は $x_+\geq 0, x_-\geq 0$ を導入し、$x=x_+ - x_-$ と置くことですべての変数を非負条件に置き換えることができます。
\begin{array}{ccc}
\begin{aligned}
\min & \quad c^T x \\
\text{s.t.} & \quad Ax = b \\
\\
\end{aligned}
&
\Leftrightarrow
&
\begin{aligned}
\min & \quad c^T x_+ - c^T x_- \\
\text{s.t.} & \quad Ax_+ - Ax_- = b \\
& \quad x_+ \geq 0, x_- \geq 0
\end{aligned}
\end{array}
この定式化についても2.4.と同じく(LP2)から(DP2)の導出が使えます。
\begin{array}{ccccc}
\begin{aligned}
\text{(LP5)} &\\
\min & \quad c^T x_+ - c^T x_- \\
\text{s.t.} & \quad Ax_+ - Ax_- = b \\
& \quad x_+ \geq 0, x_- \geq 0
\end{aligned}
&
\hspace{1em}
&
\begin{aligned}
\text{(DP5')} &\\
\max & \quad b^T y \\
\text{s.t.} & \quad A^T y \leq c\\
& \quad -A^T y \leq -c\\
\end{aligned}
&
\Leftrightarrow
&
\begin{aligned}
\text{(DP5)} &\\
\max & \quad b^T y \\
\text{s.t.} & \quad A^T y = c\\
\\
\end{aligned}
\end{array}
このことから、主問題が自由変数を含む場合、双対問題で変数に対応する制約式が等式制約になることがわかります。
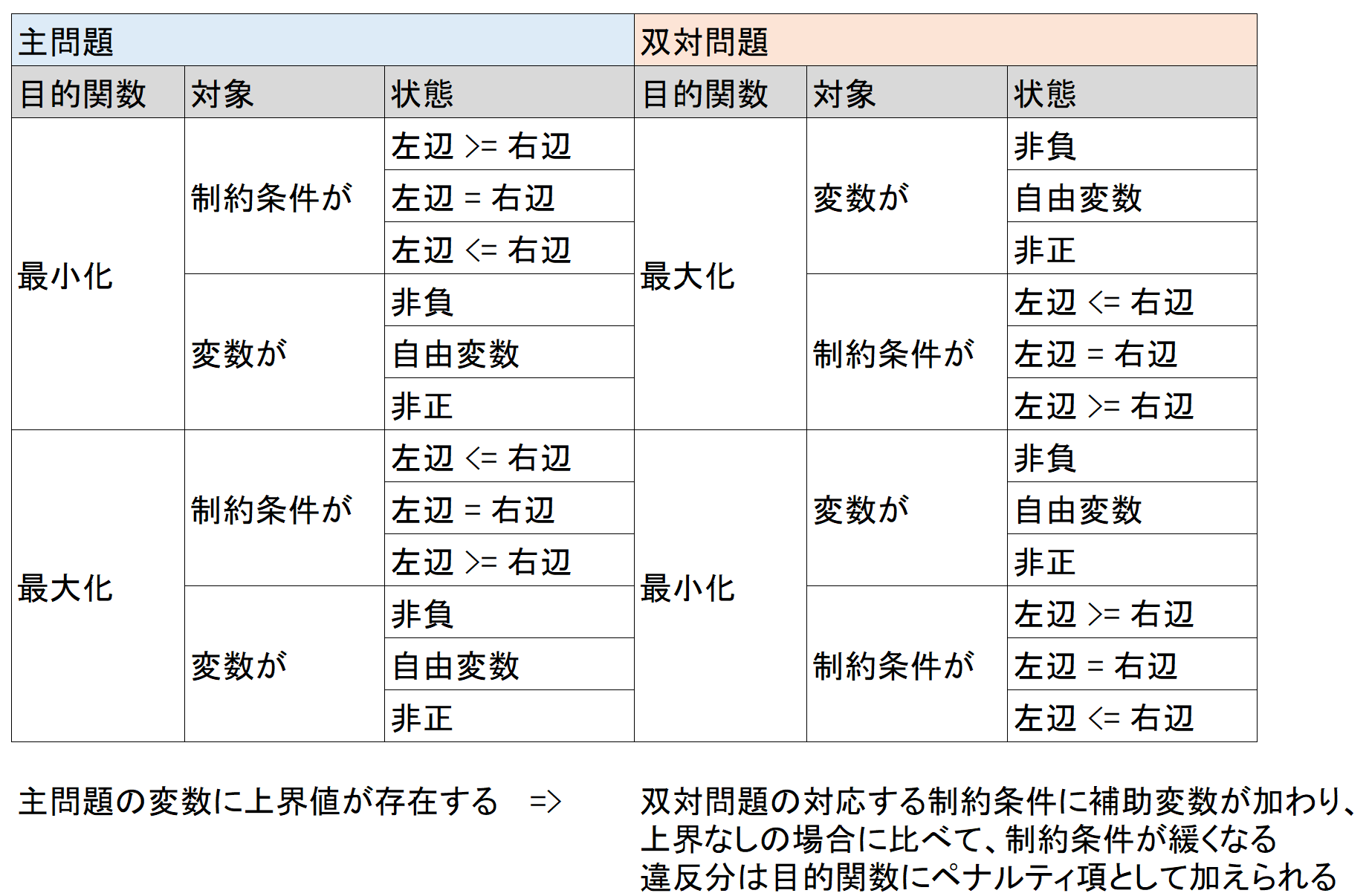
ここまでのことから、主問題の変数、制約条件の等号、不等号を見れば、双対問題の等号、不等号が推測できることがわかります。その関係は、以下の図が示す通り主問題と双対問題で変数、制約条件が入れ替わった形となっています。
2.6. 変数が上界を持つ場合
変数に上界が定められているケースの問題もよく扱います。
特に0-1整数計画問題を線形緩和した場合、$0 \leq x \leq 1$の形がよく出てきます。
この定式化も、双対問題が得やすい形に変形しますが、理解のため、2段階にわけて変形していきます。
\begin{array}{ccccc}
\begin{aligned}
\min & \quad c^T x \\
\text{s.t.} & \quad Ax = b \\
& \quad 0 \leq x \leq M \\
\\
\end{aligned}
&
\Leftrightarrow
&
\begin{aligned}
\min & \quad c^T x \\
\text{s.t.} & \quad Ax = b \\
& \quad Ix \leq M e \\
& \quad x \geq 0
\end{aligned}
&
\Leftrightarrow
&
\begin{aligned}
\min & \quad c^T x + 0 w \\
\text{s.t.} & \quad Ax = b \\
& \quad I x + I w = M e \\
& \quad x \geq 0, w \geq 0
\end{aligned}
\end{array}
まずは、標準形に書き直しやすくするため、上界の制約 $x \leq M$ を分離しました。ここで$e$はすべての要素が1のベクトルです。
単位行列をかけてもベクトルの値は変化しないので、$I x$の形に書き換えています。
また、等式制約に置き換えたいので、補助変数wを導入して等式制約に置き換えています。
この形は、変数、制約条件ともに分離した形のため、(LP2+3)から(DP2+3)への変換を行います。
\begin{array}{ccccc}
\begin{aligned}
\text{(LP6)} &\\
\min & \quad c^T x + 0 w \\
\text{s.t.} & \quad Ax = b \\
& \quad I x + I w = M e \\
& \quad x \geq 0, w \geq 0
\end{aligned}
&
\hspace{0.5em}
&
\begin{aligned}
\text{(DP6')} &\\
\max & \quad b^T y + M e^T z' \\
\text{s.t.} & \quad A^T y + I z' \leq c\\
& \quad I z' \leq 0
\end{aligned}
&
\underset{z = -z'}{\Leftrightarrow}
&
\begin{aligned}
\text{(DP6)} &\\
\max & \quad b^T y - M e^T z \\
\text{s.t.} & \quad A^T y - z \leq c\\
& \quad z \geq 0
\end{aligned}
\end{array}
得られた双対問題はやや解釈が難解です。丁寧に見ていきましょう。
(DP6)の制約条件を変形し、$z \geq A^T y_1 - c$と置くと、$z$は(DP0)の制約条件の違反ベクトルとみなせます。
そのため、(DP6)は目的関数に(DP0)からの違反分をペナルティとして組み込んだものと解釈できます。
このペナルティ項の大きさは主問題の変数の上界値 $M$ で決まります。
そのため、上界値を大きくすると制約違反が行われなくなり、(DP0)の結果に近づきます。
理論上は上界値が無限大に発散すれば、(DP6)の目的関数値は(DP0)の目的関数値に収束するため、上界制約なしの場合の結果と整合が取れています。
3. 全体のまとめ
ここまで、さまざまな形式の主問題について、双対問題の導出方法と得られた結果を見てきました。
これまでの議論をまとめると以下の表になります。
主問題の変数、制約条件の形に応じて、対応する双対問題がどのような形を取るのかが行ごとに纏まっています。
4. 最後に
今回は行列形式の線形計画問題を扱いましたが、実社会で使われる問題を定式化する場合、多くは$\Sigma$ を使った一次式(一次不等式)の組として表現されることが多いです。
例えば、最初に紹介した(LP0)、(DP0)は以下のように表現されます。
\begin{array}{ccc}
\begin{aligned}
\text{(LP0)} &\\
\min & \quad \sum_{j \in J}c_j x_j \\
\text{s.t.} & \quad \sum_{j \in J} a_{ij}x_j = b_i \quad \text{for }i \in I\\
& \quad x_j \geq 0 \quad \text{for } j \in J
\end{aligned}
&
\hspace{3em}
&
\begin{aligned}
\text{(DP0)} &\\
\max & \quad \sum_{i \in I}b_i y_i \\
\text{s.t.} & \quad \sum_{i \in I}a_{ij}y_i \leq c_j \quad \text{for }j \in J\\
\\
\end{aligned}
\end{array}
機会があれば、この$\Sigma$ 記法での双対問題の導出についても整理して、典型的な問題に対する双対問題の導出を試してみたいと思います。