BoTorchのMC獲得関数で最小化タスク解きたいとき

概要

BoTorchでモンテカルロ(MC)獲得関数を使って最小化タスクをときたいときに困った備忘録です.

BoTorchのMC獲得関数は基本的に最大化タスクを解くことを前提としています.
例えば, EIのbotorch.acquisition.monte_carlo.qExpectedImprovementの例では

MC-based batch Expected Improvement.
This computes qEI by (1) sampling the joint posterior over q points (2) evaluating the improvement over the current best for each sample (3) maximizing over q (4) averaging over the samples
qEI(X) = E(max(max Y - best_f, 0)), Y ~ f(X), where X = (x_1,…,x_q)

のように改善量が$\max(y - y_{\rm best}, 0)$で定義されていて, 最大化タスクを前提とした実装になっています.
利用時は以下のような形になります.

model = SingleTaskGP(train_X, train_Y)
best_f = train_Y.max()[0]
sampler = SobolQMCNormalSampler(1024)
qEI = qExpectedImprovement(model, best_f, sampler)
qei = qEI(test_X)

解析的獲得関数のbotorch.acquisition.analytic.ExpectedImprovementの場合は引数にmaximize (bool)があり, maximize=Falseとすることで最小化タスクを行うことができますが, MC獲得関数にはmaximizeオプションがないです.

※ 過去にPRが出ていますが, 修正範囲が大きいことと, 目的変数を反転させることで対応可能であるためマージされずCloseされています.
Add maximize option in subclasses of MCAcquisitionFunction #1321

Thanks for the PR. The reason we don't have this option is b/c this behavior is easily achievable by passing an objective that flips the sign. In particular, things get kind of weird if the model is multi-output and the objective is not simply the identity function. E.g. if we're adding a ConstrainedMCObjective then this behavior of maximize won't work as intended as it negates the constraint-penalized objective (rather than constraint penalizes the negated objective, which is what one should do in that case). So we did not add the maximize option in order to avoid these kinds of ambiguities/confusions. Does that make sense?

書いてある通りで, 目的変数の符号を反転するだけです.

実行例

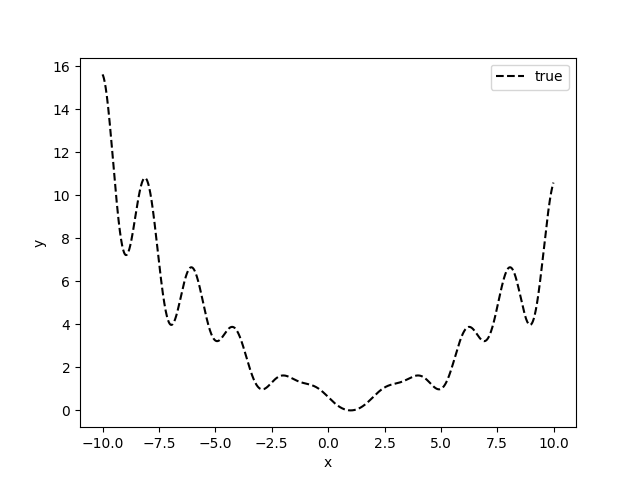
次の関数の最小値を探索します.

import torch
from botorch.test_functions.synthetic import Levy

def f(x):
    problem = Levy(dim=1)
    return torch.unsqueeze(problem(x), dim=1)
bounds = torch.tensor([[-10.0], [10.0]])

以下でoptimizerを実装しています.

from botorch.models import SingleTaskGP
from gpytorch.mlls import ExactMarginalLogLikelihood
from botorch import fit_gpytorch_model
from botorch.utils.transforms import unnormalize, normalize
from botorch.models.transforms.outcome import Standardize
from botorch.sampling.normal import SobolQMCNormalSampler
from botorch.acquisition.monte_carlo import qExpectedImprovement, qNoisyExpectedImprovement
from botorch.optim import optimize_acqf


class BayesOptimizer:
    def __init__(self):
        self.model = None
        self.sampler = SobolQMCNormalSampler(sample_shape=torch.Size([128]))

    def fit_gp(self, X, y):
        """
        GPのフィッティング
        """
        self.model = SingleTaskGP(X, y, outcome_transform=Standardize(m=1))
        mll = ExactMarginalLogLikelihood(self.model.likelihood, self.model)
        fit_gpytorch_model(mll)

    def get_candidates(self, X, y, direction, q=1):
        """
        実験候補点取得.
        Xは0-1正規化されている想定
        """
        if direction == 'minimize':
            # 最小化タスクの場合は目的変数の符号反転
            y = -y
        self.fit_gp(X, y)
    
        X_dim = X.size()[1]
        bounds = torch.zeros(2, X_dim)
        bounds[1] = 1
        # acq_func = qExpectedImprovement(model=self.model, sampler=self.sampler, best_f=y.max())
        acq_func = qNoisyExpectedImprovement(model=self.model, X_baseline=X, sampler=self.sampler, best_f=y.max())
        candidates, acq_values = optimize_acqf(acq_func, bounds=bounds, q=q, num_restarts=10, raw_samples=100)
        return candidates.detach()

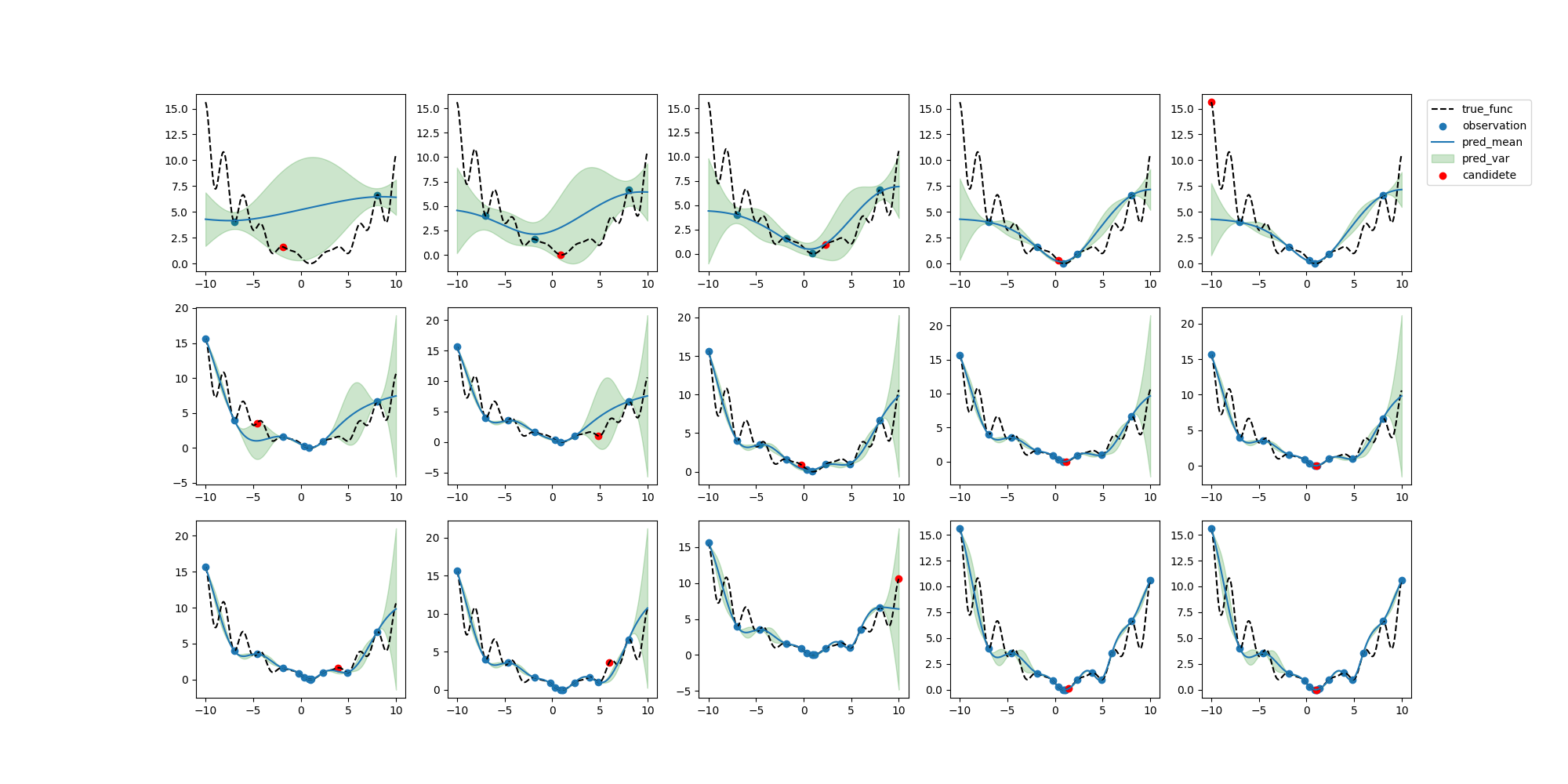
探索実行

# 初期観測データ生成
x_obj = torch.tensor([[-7], [8.0]]).double()
y_obj =f(x_obj)

for i in range(10):
    # ベイズ最適化による探索
    optimizer = BayesOptimizer()
    x_obj_norm = normalize(x_obj, bounds)
    x_candidates = optimizer.get_candidates(x_obj_norm, y_obj, direction='minimize')
    x_candidates = unnormalize(x_candidates, bounds)
    # 候補点の観測
    y_candidates = f(x_candidates)
    # 観測データに追加
    x_obj = torch.cat([x_obj, x_candidates])
    y_obj = torch.cat([y_obj, y_candidates])

探索経過をプロットすると以下のようになります.

参考文献

• https://botorch.org/api/acquisition.html#botorch.acquisition.monte_carlo.qExpectedImprovement