はじめに
タイトルが長い!!!!
ですがよろしくお願いします。
今回 明治大学Advent Calendar 2018 2回目の投稿になります![]() 。
。
最近授業でMATLABを多く使うようになったのですが、便利だなぁと思うのと同時に
あれ?MATLABを駆使すれば数学オリンピックの問題もすぐ解けるのでは、、、?
と思いましたので、やってみようと思います。
※今回使用させていただく問題、内容は、数学オリンピック財団のサイト
から引用、参考にさせていただいています。
概要
- 数学オリンピックについて述べる
- MATLABを使って実際の問題を解いてみる
- 私の数学オリンピックに挑戦した感想を述べる
数学オリンピックって?
まずは、数学オリンピックについて述べたいと思います。
今回は特に、**日本数学オリンピック(JMO)**について述べます。
日本数学オリンピック
日本数学オリンピック(JMO)は毎年1月(成人の日)に予選が行われ、予選通過者が2月の本選に進みます。その後本選や合宿などを通して、国際数学オリンピック(IMO)に出場する人が選ばれます。
誰でも出れるわけではなく、募集要項には
大学教育を受けていない満20未満の者
と書いてあります。つまりもう私は受けられません、、トホホ![]() 。
。
多くの人は高校1,2年生です。(中学生ももちろん受けられます)。
予選と本選
予選
予選は3時間で12問のテストです。答え方は短答式です。つまり途中式とかいらないから、答えだけ書いて正解ならオッケー!ということです。
なので予選では証明の問題は出ません。
幾何や整数論、組み合わせ、式変形の問題が多い印象です。
(積分の問題は範囲外です)
年によって異なりますが、だいたい7,8問正解できればAランク合格となり、本選に進むむことができます。さらに3,4問でも正解できればBランク合格となります。Bランクでは本選に進むことはできませんが、Bランクの中でも上位の人は地区表彰をもらえるチャンスがあります。
(実際は12点満点ですが、まぁまず12問目は超難問です。ですので、だいたい10問くらいから解ける問題を頑張る!という感じです。)
本選
予選の時間、3時間もなかなか長いですが、本選は記述式で、なんと
全5問 4時間です。ナゲェ
(私はかつて大学入試で「4問 2.5時間」のテストをしたことがありますが、それに比にならないくらい1問に対する時間の割合が大きいです、、)
私は本選まで進んだことはないのですが、本選に進んだ友達曰く
「問題のレベル全くが違う、、、」
と言っていました。。。
というわけで、今回は短答式である、予選の問題をやってみようと思います!
MATLABで解くぞー!!!
JMO 2016 第1、2問
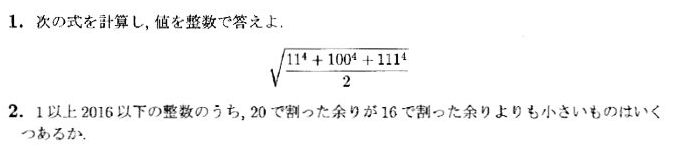
(http://www.imojp.org/challenge/old/jmo26yq.html)
どうですか、1問目からこの計算
4乗はなんとか計算できそうですけど、その後に根号を外すのが大変そう、、
(この問題、実際は簡単に計算できる方法があります。)
というわけで。
MATLABでプログラム書いてみた
%2016数オリ予選1,2問%
%1問目は普通に計算させる%
sqrt((11^4+100^4+111^4)/(2))
%2問目は順に数を調べて、数え上げる%
S=0;
for i=1:2016
if (mod(i,20)<mod(i,16))
S=S+1;
end
end
%Sが求める答え%
S
そして、出力はこちら
ans =
11221
S =
600
つまり、答えは11221と600個
うん
どっちも合ってたわ、正解だわ。
これMATLABで行けるわ。
さすがですね、ゴリ押しで解けちゃいました。
というわけで他の問題もさっくり解けるのでは??
やってみよう!!
JMO 2016 第9問
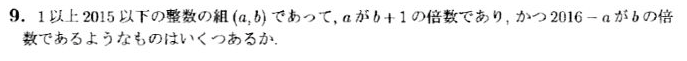
(http://www.imojp.org/challenge/old/jmo26yq.html)
この問題、本来なら色々考察をして解かなければいけないのですが、MATLABならどうでしょう。
というわけで書いてみました
%2016数オリ予選9問%
%最初から順に調べて確認させる%
S=0;
for a=1:2015
for b=1:2015
if((mod(a,b+1)==0)&&(mod(2016-a,b))==0)
S=S+1;
end
end
end
%答えを出力させる%
S
出力はこちら
S =
1980
つまり答えは1980個うん、合ってます。出来ちゃいました。
これやっぱりMATLAB使えば解けるのでは??
よーし、どんどんやってみよう!!
JMO 2018 第4問
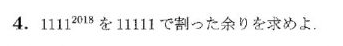
(http://www.imojp.org/challenge/old/jmo28yq.html)
よーし!やるぞー!!
%2018数オリ予選4問%
A=1111^2018;
mod(A,11111)
短い、すぐ終わる。
出力はこちら
ans =
NaN
、
、
、
、
あ、あれっ??
答えが、、、でない、、!?
それはそうだよね
$1111^{2018}$は、常用対数を用いて桁数を調べると**6147桁!!**そりゃ、パソコンが全部計算できるわけないですよね、、、
(実際MALTAB上では$1111^{2018}$は「Inf」と表示されてしまいます。)
このように、数学オリンピックの問題は、真面目にやると値がとても大きくなるような数が出てきます(特に整数論は2018乗のように西暦の数だけ累乗させるのが大好きみたいです)。そしてそれをうまく工夫することで計算、考え方を簡単にして解くわけです。ほとんどの問題はゴリ押しでは到底計算できません
さらに、答えに根号が入っているような問題は、普通はMATLABで解くことができません(そのまま数値で出てきてしまうので根号を含めることができない)。というかまず幾何の問題だって解けません。
というわけで
多分MATLABでは予選通過できない!!!
ちゃんちゃん![]()
、
、
、
せっかくなので
1問くらいはちゃんと解答を書いてみようと思います。
JMO 2015 第5問
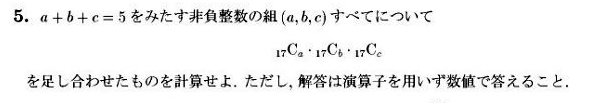
(http://www.imojp.org/challenge/old/jmo24yq.html)
この問題をやってみようと思います。
①まずはMATLABで
%2015数オリ第5問%
%答えを入れておくための変数を用意%
S=0;
%当てはまる組み合わせを調べて、全部計算させる%
for a=0:5
for b=0:(5-a)
S=S+nchoosek(17,a)*nchoosek(17,b)*nchoosek(17,(5-a-b));
end
end
S
(MATLABにはコンビーネーションを計算するコマンドがあるのでプログラムが短くて済みます。やったね!)
出力はこちら
S =
2349060
というわけで、正解は2349060でした。
②自分で解いてみる
それでは解答を考えてみましょう。
まず、問題を見ると、コンビーネーションCの数字に17が書いてありますね、、ウワァ計算が大変そう、、、
しかしよく考えると$a+b+c=5$を満たす非負整数$(a,b,c)$の組みはあまりないような気がします。(実際に計算すると21通りです)
しかも、どのコンビネーションも
$${}_{17} C$$
となっているので、例えば$(a,b,c)=(0,0,5)$の時と、$(a,b,c)=(5,0,0)$の時の
$$_{17}C_a \cdot _{17}C _b \cdot _{17}C _c $$
の値は変わりません。
つまり、どの文字ににどの数字が当てはまるか、というより5という数字の分け方に注目すれば良いというのがわかります。
数字の分け方だけなら5パターンしかないので、そこまで複雑にはなりませんね。というわけで計算してみましょう。
解答
(ア)数字の分け方が**(5,0,0)**のとき
この場合、$a,b,c$に数字を当てはめる場合の数は3通りなので
\cdot _{17}C_a \cdot _{17}C _b \cdot _{17}C _c=3 \cdot _{17}C_5 \cdot _{17}C _0 \cdot _{17}C _0 = 18564
(イ)数字の分け方が**(4,1,0)**のとき
この場合、$a,b,c$に数字を当てはめる場合の数は6通りなので
$$_{17}C_a \cdot _{17}C _b \cdot _{17}C _c=6 \cdot _{17}C_4 \cdot _{17}C _1 \cdot _{17}C _0 = 242760$$
(ウ)数字の分け方が**(3,2,0)**のとき
この場合、$a,b,c$に数字を当てはめる場合の数は6通りなので
$$_{17}C_a \cdot _{17}C _b \cdot _{17}C _c=6 \cdot _{17}C_3 \cdot _{17}C _2 \cdot _{17}C _0 = 554880$$
(エ)数字の分け方が**(3,1,1)**のとき
この場合、$a,b,c$に数字を当てはめる場合の数は3通りなので
$$_{17}C_a \cdot _{17}C _b \cdot _{17}C _c=3 \cdot _{17}C_3 \cdot _{17}C _1 \cdot _{17}C _1 = 589560$$
(オ)数字の分け方が**(2,2,1)**のとき
この場合、$a,b,c$に数字を当てはめる場合の数は3通りなので
$$_{17}C_a \cdot _{17}C _b \cdot _{17}C _c=3 \cdot _{17}C_2 \cdot _{17}C _2 \cdot _{17}C _1 = 943296$$
(ア)~(オ)で求めた数を全て足して
$$18564+242760+554880+589560+943296=2349060$$
となり、答えが出てきました。
③ もっと簡単に求めたい!
先ほどの解答でも一応答えは求まりますが、計算量が多いですよね、、、これだと計算ミスしてしまいそう、、
いろいろ調べていたら、数学オリンピックの過去問集[1]にもっと簡潔な解答があったので、紹介しょうと思います。
解答
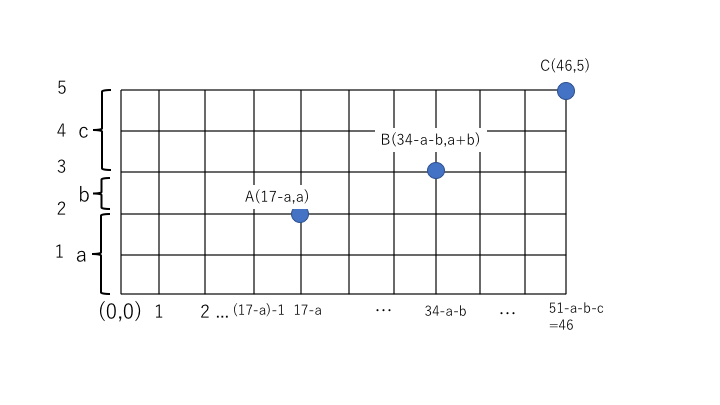
このとき
$$A(17-a,a),B(34-a-b,a+b),C(51-a-b-c,a+b+c)$$
となるが、$a+b+c=5$であることから、
$$C(46,5)$$
であることが分かる。
原点$(0,0)$から2点A,Bを通って点Cに行く最短経路の場合の数は
_{17}C_a \cdot_{17-a}C_{17-a} \times _{17}C_b \cdot _{17-b}C _{17-b} \times _{17}C_c \cdot _{17-c}C_{17-c}
=_{17}C_a \cdot _{17}C_{b} \cdot _{17}C_c
となる。
ここで$a+b+c=5$を満たす全ての$a,,b,c$について$_{17}C_a \cdot _{17}C _b \cdot _{17}C _c$を考えると、この数の総和は原点$(0,0)$から点$C(46,5)$に向かう最短経路の場合の数と等しくなる。したがって、求める答えは
_{51}C_5=2349060
き、綺麗にまとまっていて美しい、、
私が考えた計算方法よりも圧倒的にすっきりしていますね、、
ただ、この考えを解答時間内に思いつけるのでしょうか、、
私ならこんな上手な方法を思いつく前に**(解法分かったし、計算すれば答え出るぞ!!)**と一目散にコンビネーションの計算をしてますね、、笑
(解法がすぐ分かる問題の方が少ないので、思い立ったら計算しまくって答えを求めるのも良いと思います。なんせ3時間ありますから。)
「最短経路」なんて問題文には一言も書いていないですから、この発想が出るだけでも相当数学に長けていると思います。
まとめ
MATLABでも解ける問題はある。ただ少ない。
数学オリンピックの問題は、工夫を見つけることで、比較的楽に計算できる!
しかし、その工夫の仕方が難しくて、見つけるのがとても大変。
でもとっても楽しい!!数オリ最高!!
最後に、、、数オリの感想
はじめの方にも少し書きましたが、私は本選に進んだことはありません。
2014,2015年に受けましたが、それぞれ1点のCランクと4点のBランクです。
(いくらなんでも1点はやばいですね、、笑)
2015年の方は、2問ほど計算ミスで落としてしまい、(あぁ、なんであんなミスをしたんだ、、)と予選帰りの電車で落ち込んでました。実際のところ6点だった友達が地区表彰をもらっていたので、とても悔しかったです。。。
しかし、数学オリンピックの解答時間中、**夢中で計算したり、考えたりする時間がとっても楽しくて。**あぁ、私は数学が好きだったんだな、と自覚させてくれました。私が今、数学系の勉強をしているのも、数学オリンピックのおかげです。
ありがとう、数オリ!
参考文献 引用
[1] 公益財団法人 数学オリンピック財団 監修『数学オリンピック2014~2018』日本評論社.
数学オリンピック財団 国内大会 国際大会の過去問
http://www.imojp.org/challenge/