Bカーブの可変抵抗の入力値を使って擬似的にAカーブのようなデータを取り出す

可変抵抗の種類について

可変抵抗には抵抗値の変化の特性によって、Aカーブ、Bカーブ、Cカーブといった主に3種類のものが存在するようです。
一般的にはAカーブ、Bカーブのものがよく使われるようですが、用途毎に準備しておくのも無駄ですし、Amazon等で安く購入できる物はBカーブのものが多い印象です。

都合によりAカーブのような特性をもたせたかったのですが手元にBカーブの可変抵抗しか持ち合わせていなかったので、計算式を用いて擬似的にAカーブ、それも任意のカーブ具合に調整できないか考えてみました。

計算式

前提

RaspberryPi等で、12bitのA-Dコンバータ経由で可変抵抗の値を取得する場合を想定しています。
私の場合はRaspberryPi4BとMCP3208-CI/Pを使用しました。

Bカーブの可変抵抗をそのまま使用する場合の計算式

$y＝a\ x$
ここで、$x$は12bitなので0～4095まで変化します。この変化量はBカーブなので、回転角度増加とリニアに連動します。
もし、求める値$y$の範囲を0～100としたい場合は、
$y=x/4095\times100$
とします。

yの値をAカーブ的に変化させる場合の計算式

$y=a\ x^n$
このように、$n$乗を追加するだけです。
ただ、これだけでは$n$の値によって求める$y$の範囲が大きく変動してしまいますので、求める値$y$の範囲を0～100としたい場合は
$y= x^n / 4095^n \times 100$
とします。

nの値について

上記の式において、$n$の値を変更することによりカーブの具合を調整することができます。
具体的には$n$の値が1に近づくほどBカーブ（直線的）に近くなり、大きくなればなるほどカーブがきつくなります。
下の図のように$n$を2,2.5,3と大きくするにつれてカーブがきつくなるのがわかると思います。

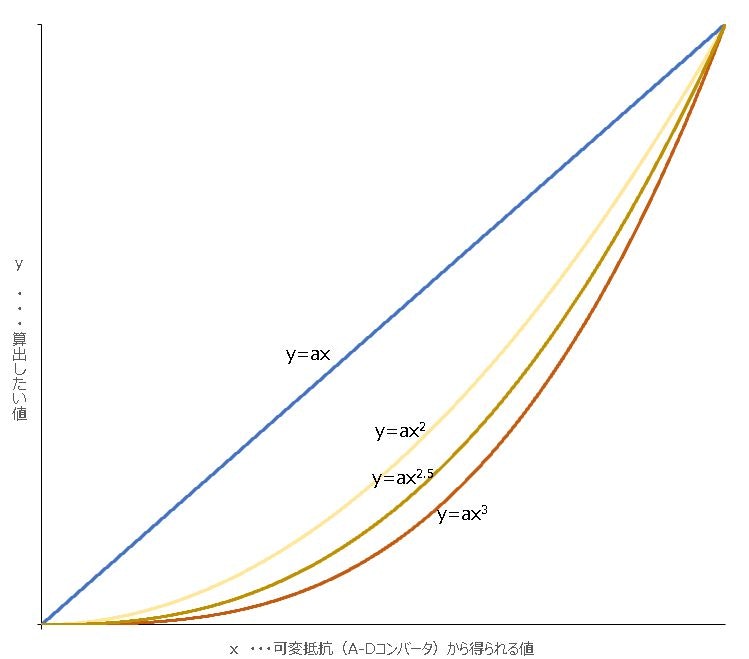
通常のAカーブの可変抵抗を使用する場合と比べ、このカーブの具合を任意で調整できるところが利点かと思います。

Pythonでの記述例

EXPO = 2.5     #ここの値を修正
SRANGE = 4095  #可変抵抗からの入力最大値
RRANGE = 100   #計算により求める値の最大値

  iv0 = Decimal(str(ここに可変抵抗からの入力値 ** EXPO / SRANGE ** EXPO * RRANGE ))
  i0  = str(iv0.quantize(Decimal('0.1'), rounding=ROUND_HALF_UP)) #四捨五入する桁を指定

※私が使用したケースでは最後に文字列として出力したかったため、最終行で文字列に変換しています。