統計検定を受けるのでRで統計学を基礎から勉強していく の続きです。
今回は2次元のデータの相関関係と回帰分析を取り上げます。
2次元のデータ
2つの変数$x$, $y$ からなる組 $(x, y)$ を観測して一連の観測値 $(x_1, y_1), (x_2, y_2), ..., (x_n, y_n)$ を得る場合、データ $\{(x_i, y_i)\}$ を 2次元のデータ という。
相関と回帰
-
2次元のデータについて、変数 $x$, $y$ を対等のものと見る見方を 相関 という。
$x$, $y$ の相互関係を調べるのが中心。→ 相関関係 -
2次元のデータについて、変数 $y$ が $x$ に(あるいは $x$ が $y$ に) 従っているものと見る見方を 回帰 という。
$y$ が $x$ から決定される様子や程度を調べるのが基本。→ 回帰分析
相関関係
散布図
2次元のデータを$\{(x, y)\}$ を $x-y$ 平面上の $n$ 個の点として図示したものを 散布図 という。
例
9人のメンバーの身長 $x$とバスト $y$ を測定した時の2次元データを
{(157, 78), (162, 88), (159, 80),
(159, 76), (155, 75), (161, 78),
(159, 90), (156, 82), (154, 74)}
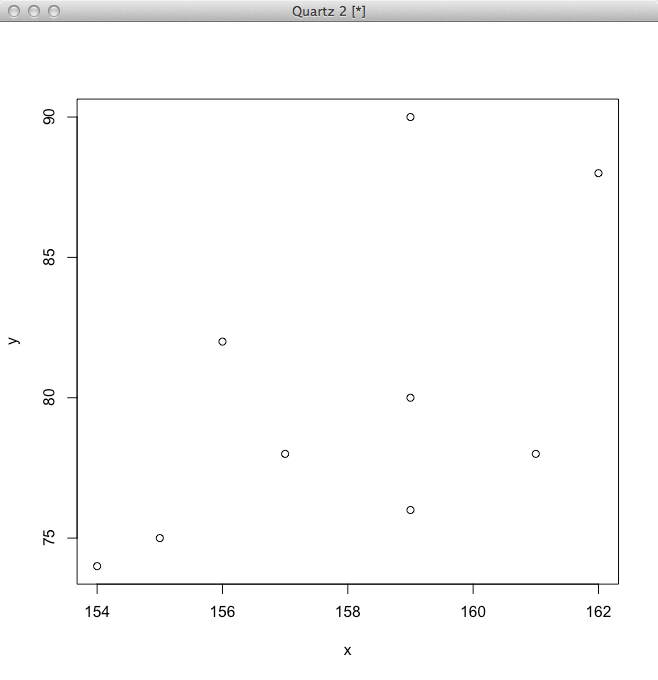
とする。このデータの散布図を R で描くには以下のようにする。
> # まず身長とバストをそれぞれベクトルとして入力する
> x <- c(157, 162, 159, 159, 155, 161, 159, 156, 154)
> y <- c(78, 88, 80, 76, 75, 78, 90, 82, 74)
> # plot(x, y) 関数でプロットを行う
> plot(x, y)
相関係数
2次元のデータ $\{(x_i, y_i)\}$ について $x$ が増加すると $y$ も増加する、などの相関関係があるかどうかを調べる際に、相関の程度を示す指標として使われるのが ピアソンの 積率相関係数、あるいは単に相関係数とよばれるものである。
相関係数$r_{xy}$は以下のように定義される:
r_{xy} := \frac{\sum(x_i - \bar{x})(y_i - \bar{y})/n}{\sqrt{\sum(x_i - \bar{x})^2/n}\sqrt{\sum(y_i - \bar{y})^2/n}}
= \frac{\sum(x_i - \bar{x})(y_i - \bar{y})}{\sqrt{\sum(x_i - \bar{x})^2}\sqrt{\sum(y_i - \bar{y})^2}}
ここで、中央の式の分母は変数 $x$, $y$ の標準偏差 $\sigma_x$, $\sigma_y$ の積である。分子は $x$ の偏差 $x - x_i$ と $y$ の偏差 $y - y_i$ を同時に考えた時の平均でありこれを 共分散 (covariance) とよぶ。共分散を $\sigma_{xy}^2$と書けば、相関係数は
r_{xy} = \frac{\sigma_{xy}^2}{\sigma_x \sigma_y}
と書ける。相関係数は $ -1 \leq r_{xy} \leq 1 $ の値を取る。
- $r_{xy} > 0$ のとき、この2次元データには 正の相関 があるという。
- $r_{xy} < 0$ のとき、この2次元データには 負の相関 があるという。
R で実習
まずは定義に従って相関係数を計算してみる。
> # x の標準偏差を求める
> sigma_x = sqrt(mean((x - mean(x))^2))
> sigma_x
[1] 2.538591
> # y の標準偏差を求める
> sigma_y = sqrt(mean((y - mean(y))^2))
> sigma_y
[1] 5.300827
> # x と y の共分散を求める
> sigma_xy2 = mean( (x - mean(x)) * (y - mean(y)) )
> sigma_xy2
[1] 7.666667
> # 相関係数を計算する
> r_xy = sigma_xy2 / (sigma_x * sigma_y)
> r_xy
[1] 0.5697315
次に、相関関数を計算する関数を使ってみる。
># cor() 関数の method 引数に "pearson" を指定することでピアソンの相関係数が計算できる。
> cor(x, y, method="pearson")
[1] 0.5697315
$r_{xy} = 0.5697315 $ と求まり、メンバーの身長とバストの間には弱い正の相関があることがうかがわれる。
回帰
最小二乗法
2次元のデータ $\{(x_i, y_i)\}$ を回帰の視点から見るとする。$y$ が $x$ にしたがって決定される関係があるとき、$x$ を 独立変数 (independent variable), $y$ を 従属変数 (dependent variable) という。この関係がおおよそ、一次式
y = a x + b
で説明されると仮定するときに、係数 $a$, $b$ の値をどのように決めるのが最適であるか?
最小二乗法 (method of least squares) は各点 $(x_i, y_i)$ の直線 $y(x) = a x + b$ からの $y$ 座標についての隔たり $y_i - y(x_i)$ の二乗の和が最小となるように $a$, $b$ を決定する方法である。
すなわち、二乗の和 $L(a, b)$ を
L(a, b) := \sum_{i=1}^n (y_i - y(x_i))^2 = \sum_{i=1}^n (y_i - (a x_i + b))^2
と定義した時に、$L(a, b)$ を最小にするように $a$, $b$ を決めればよい。
それには $L$ を $a$, $b$ で偏微分してそれぞれ 0 とおいた方程式を解けばよい。
結果だけ書くと、
a = \frac{\sum x_i y_i - n \bar{x} \bar{y}}{\sum x_i^2 - n \bar{x}^2}, \\
b = \bar{y} - a \bar{x} .
得られた直線の方程式を $y$ の $x$ 上への 回帰直線 あるいは 回帰方程式 という。
R で実習
身長とバストのデータ $\{(x_i, y_i)\}$ について回帰直線を求めてみる。
> # まずは定義に従って計算する。
> n = length(x)
> a = (sum(x * y) - n * mean(x) * mean(y)) / (sum(x^2) - n * mean(x)^2)
> b = mean(y) - a * mean(x)
> c(a, b)
[1] 1.189655 -107.854406
> # つぎに、Rの関数 lsfit(x, y) を使って求めてみる。
> f <- lsfit(x, y)
> f$coefficients # 係数を見る。
Intercept X
-107.854406 1.189655
散布図に回帰直線を重ねて描くには、上の計算結果 a, b を使って、
> plot(x, y) # まず散布図を描く
> abline(b, a) # 回帰直線を引く。第一引数が切片、第二引数が傾き
とすればよい。または、lsfit(x, y) の計算結果 f を使って、
> abline(f)
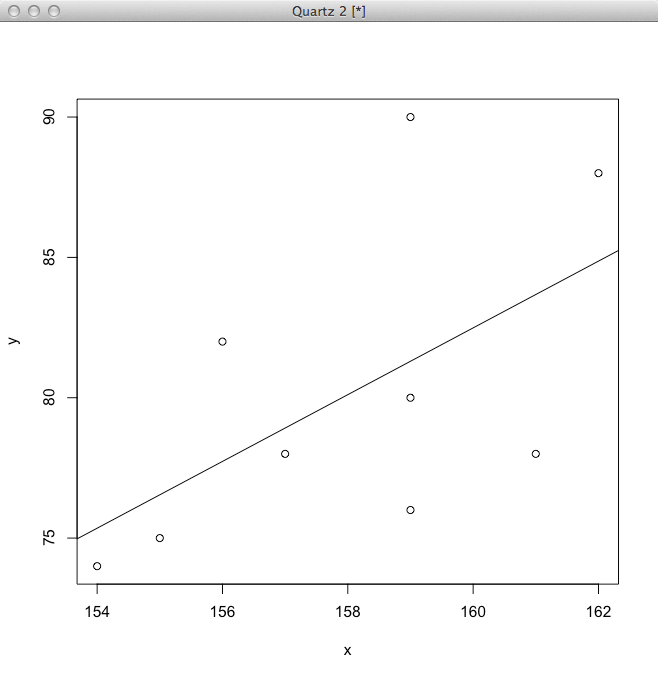
としてもよい。結果、下の図が得られる。
このデータは相関関係が弱いため、回帰直線を求める意味が薄いことに注意すること。