確率
事象$A$と$B$が独立であるとき。
P(A \cap B)=P(A)P(B)\\
加法定理 P(A \cap B)=P(A)+P(B)-P(A \cup B)\\
事象$A$と$B$が排反であるとき。
P(A \cap B)=P(\phi)=0\\
条件付き確率
ある事象$B$が起こるという条件のもとで、別のある事象$A$が起こる確率のこと。
P(A | B)=\frac{P(A \cap B)}{P(B)}\\
乗法定理 P(A \cap B)=P(B) \times P(A | B)\\
乗法定理 P(A \cap B)=P(A) \times P(B | A)\\
ベイズの定理
P\left(B_{i} | A\right)=\frac{P\left(A \cap B_{i}\right)}{P(A)}\\
P\left(B_{i} | A\right)=\frac{P\left(A \cap B_{i}\right)}{P(A)}=\frac{P\left(B_{i}\right) P\left(A | B_{i}\right)}{P(A)}\\
P\left(B_{i} | A\right)=\frac{P\left(A \cap B_{i}\right)}{P(A)}=\frac{P\left(B_{i}\right) P\left(A | B_{i}\right)}{P\left(A \cap B_{1}\right)+P\left(A \cap B_{2}\right)+\cdots+P\left(A \cap B_{k}\right)}\\
P\left(B_{i} | A\right)=\frac{P\left(B_{i}\right) P\left(A | B_{i}\right)}{P\left(A \cap B_{1}\right)+P\left(A \cap B_{2}\right)+\cdots+P\left(A \cap B_{k}\right)}=\frac{P\left(B_{i}\right) P\left(A | B_{i}\right)}{\sum_{j=1}^{k} P\left(B_{j}\right) P\left(A | B_{j}\right)}\\
確率質量関数
離散型確率変数$X$について、ある関数$p(x)$が下式を満たすとき、$p(x)$は$X$についての確率質量関数となる。
1 \geq p(x) \geq 0, \hspace{20px} \sum_{i=1}^{\infty} p(x_i) = 1\\
P(a \leq x \leq b) = \sum_{i=a}^b p(x_i)\\
確率密度関数
連続型確率変数$X$について、ある関数$y=f(x)$が下式を満たすとき、$f(x)$は$X$についての確率密度関数となる。
確率変数がある一点の値をとる確率は0になることから、”ある範囲”をとることで確率を求める。
f(x) \geq 0, \hspace{20px} \int_{-{\infty}}^{\infty} f(x)dx = 1\\
P(a \leq x \leq b) = \int_a^b f(x)dx\\
累積分布関数
累積分布関数とは「確率変数$X$がある値$x$以下の値となる確率」を表す関数。
F(x) = P(X \leq x)
離散型確率変数の場合
F(x) = P(X \leq x) = \sum_{X\leq x}P(X)\\
期待値 E(X)=\sum_{i=1}^{n} x_{i} \times p_{i}\\
分散V (X)=\sum_{i=1}^{n}\left(x_{i}-\mu\right)^{2} p_{i}\\
連続型確率変数の場合
F(x) = P(X \leq x) = \int_{-\infty}^{x}f(t)dt\\
期待値 E(X)=\int_{-\infty}^{\infty} x f(x) d x\\
分散 V(X)=E[(x-\mu)^{2}]=\int_{-\infty}^{\infty}(x-\mu)^{2} f(x) d x\\
k次モーメント E[(x-\mu)^{k}]=\int_{-\infty}^{\infty}(x-\mu)^{k} f(x) d x\\
分散を期待値から求める
\begin{aligned}
V(X) &=\int_{-\infty}^{\infty}(X-\mu)^{2} f(X) d X \\
&=\int_{-\infty}^{\infty}\left(X^{2}-2 X \mu+\mu^{2}\right) f(X) d X \\
&=\int_{-\infty}^{\infty} X^{2} f(X) d X-\int_{-\infty}^{\infty} 2 X \mu f(X) d X+\int_{-\infty}^{\infty} \mu^{2} f(X) d X \\
&=E\left(X^{2}\right)-2 \mu \int_{-\infty}^{\infty} X f(X) d X+\mu^{2} \\
&=E\left(X^{2}\right)-2 \mu \times E(X)+\mu^{2} \\
&=E\left(X^{2}\right)-2\{E(X)\}^{2}+\{E(X)\}^{2} \\
V(X) &=E\left(X^{2}\right)-\{E(X)\}^{2}
\end{aligned}
確率分布
正規分布
平均を$μ$・分散を$σ^2$とした場合に以下の確率密度関数で表される連続型確率分布。$X \sim \mathcal{N}(μ, σ^2)$と表記されます。
f(x)=\frac{1}{\sqrt{2 \pi} \sigma} \exp \left(-\frac{(x-\mu)^{2}}{2 \sigma^{2}}\right) \quad(-\infty<x<\infty)\\
\begin{aligned}
期待値 &E(X)=\mu\\
分散 &V(X)=\sigma^{2}
\end{aligned}
正規分布の再生性
2つの独立な正規分布に従うデータを足したデータ。
N\left(\mu_{1}+\mu_{2}, \sigma_{1}^{2}+\sigma_{2}^{2}\right)
標準正規分布
「平均$μ=0$、分散$σ^2=1$」の正規分布のこと。$X \sim \mathcal{N}(0, 1^2)$と表記されます。
f(x)=\frac{1}{\sqrt{2 \pi}} \exp \left(-\frac{x^{2}}{2}\right) \quad(-\infty<x<\infty)
標準化
ある確率変数Xが正規分布に従うとき、標準化を行えば「平均が0、分散が1の標準正規分布」に従う。
z=\frac{X-\mu}{\sigma}
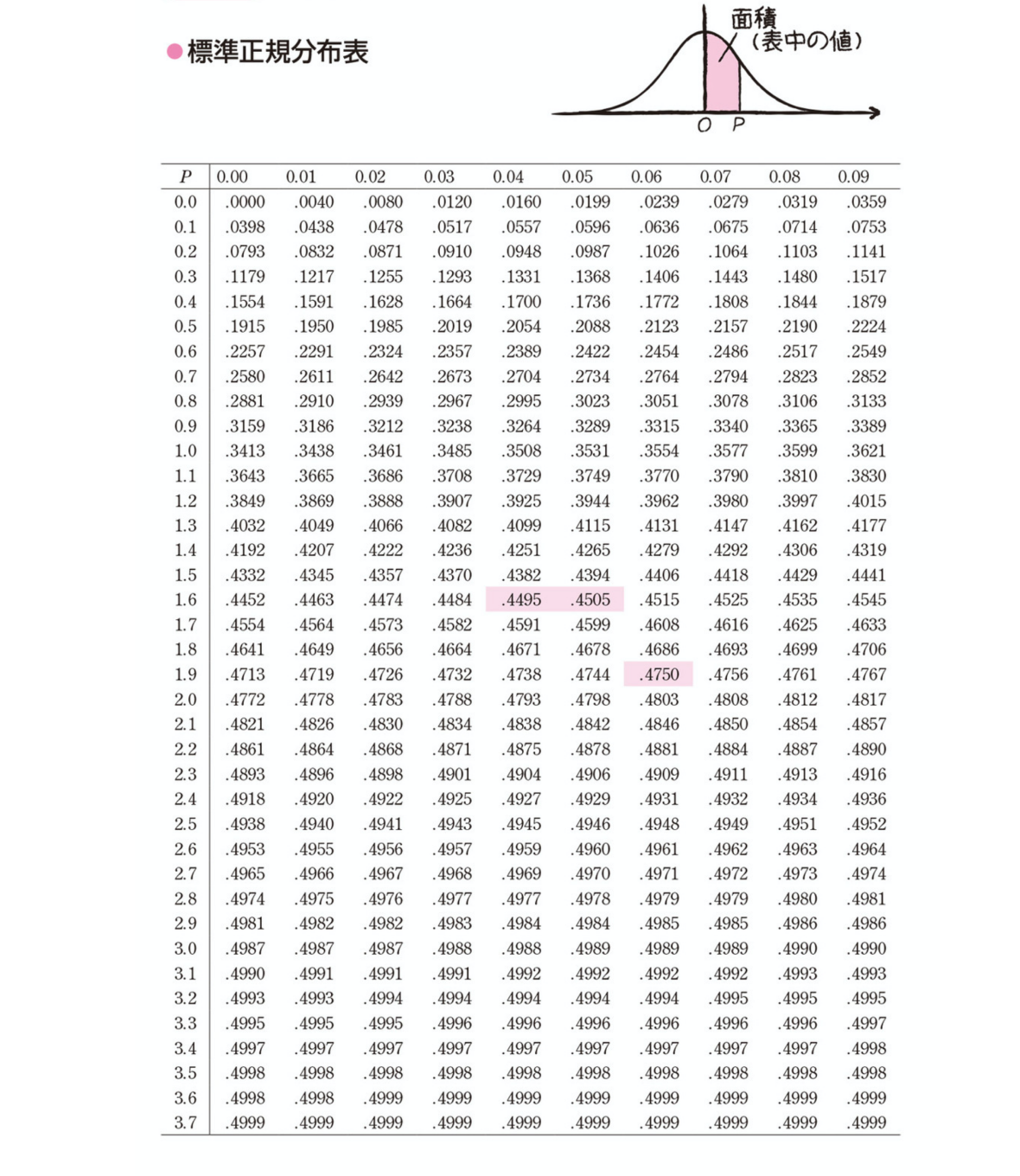
標準正規分布表
二項分布
ベルヌーイ試行を$n$回行って、成功する回数$X$が従う離散型確率分布。$X \sim \mathcal{Bin}(n, p)$と表記されます。
$n$がある程度大きい時、中心極限定理より、$\mathcal{Bin}(n, p)$は正規分布$N(np,np(1-p))$に近似できる。
P(X=k)=_{n} \mathrm{C}_{k} p^{k}(1-p)^{n-k} \quad(k=0,1,2, \cdots, n)\\
\begin{aligned}
期待値 &E(X)=n p\\
分散 &V(X)=n p(1-p)
\end{aligned}
ベルヌーイ試行
何かを行ったときに起こる結果が2つしかない試行のこと。
確率変数$X$がとる値を「1」、もう一方の結果を「失敗」とし、
確率変数$X$がとる値を「0」とします。
\begin{aligned}
&P(X=1)=p\\
&P(X=0)=1-p
\end{aligned}
ポアソン分布
ある期間に平均$λ$回起こる現象が、ある期間に$X$回起きる確率の離散型確率分布。$X \sim \mathcal{Po}(λ)$と表記されます。
P(X=k)=\frac{e^{-\lambda} \lambda^{k}}{k !} \quad(k=0,1,2, \cdots)\\
\begin{aligned}
期待値 &E(X)=\lambda\\
分散 &V(X)=\lambda
\end{aligned}
指数分布
次に何かが起こるまでの期間が従う連続型確率分布。$X \sim \rm{Ex}(λ)$と表記されます。
f(x)=\left\{\begin{array}{ll}
\lambda e^{-\lambda x} & x \geq 0 \\
0 & x<0
\end{array}\right.\\
F(x)=P(X \leq x)=\int_{-\infty}^{x} f(t) d t=\int_{0}^{x} \lambda e^{-\lambda t} d t=1-e^{-\lambda x}\\
\begin{array}{l}
期待値 E(X)=\frac{1}{\lambda} \\
分散 V(X)=\frac{1}{\lambda^{2}}
\end{array}\\
幾何分布
成功確率$p$がである独立なベルヌーイ試行を繰り返す時、初めて成功するまでの試行回数$X$が従う離散型確率分布。
P(X=k)=(1-p)^{k-1} p \quad(k=1,2,3, \cdots)\\
\begin{aligned}
期待値 &E(X)=\frac{1}{p}\\
分散 &V(X)=\frac{1-p}{p^{2}}
\end{aligned}
一様分布
離散一様分布
すべての事象の起こる確率が等しい離散型確率分布。
P(X=k)=\frac{1}{N} \quad(k=1,2, \cdots, N)\\
\begin{aligned}
期待値 &E(X)=\frac{N+1}{2}\\
分散 &V(X)=\frac{N^{2}-1}{12}
\end{aligned}
連続一様分布
確率変数$X$がどのような値でも、その時の確率密度関数$f(x)$が一定の値をとる連続型確率分布。
\begin{aligned}
&f(x)=\frac{1}{b-a} \quad(a \leq X \leq b)\\
&f(x)=0 \quad(X<a, X>b)
\end{aligned}\\
\begin{aligned}
期待値 &E(X)=\frac{a+b}{2}\\
分散 &V(X)=\frac{(b-a)^{2}}{12}
\end{aligned}
累積分布関数を用いて算出する場合
F(x)=P(-\infty \leq X \leq x)=\frac{x-a}{b-a}
標本分布
t分布
標準正規分布$N(0, 1)$に従う$Z$と自由度$n$のカイ二乗分布$W$があり、
これらが互いに独立であるとき、次の式から算出される$t$は自由度$n$の$t$分布に従います。
自由度を大きくすると標準正規分布に近づく。
t=\frac{Z}{\sqrt{\frac{W}{n}}}\\
\begin{array}{c}
期待値 E(X)=0 \quad(m>1) \\
分散 V(X)=\frac{m}{m-2} \quad(m>2)
\end{array}
t分布のパーセント点

カイ二乗分布
$Z_1,Z_2,…,Z_k$が互いに独立で標準正規分布$N(0, 1)$に従う確率変数であるときに、
次の式から算出される自由度$k$の$\chi^{2}$が従う連続型確率分布。
\chi^{2}=Z_{1}^{2}+Z_{2}^{2}+\cdots+Z_{k}^{2}\\
\begin{array}{l}
期待値 E(X)=k \\
分散 V(X)=2 k
\end{array}
カイ二乗分布の再生性
2つの確立変数$X_1,X_2$がそれぞれ独立に自由度$k_1,k_2$のカイ二乗分布に従うデータを足したデータ。
\chi^{2}(k_1+k_2)
正規分布に従う母集団からの無作為標本
確率変数$X_1,X_2,…,X_k$がそれぞれ独立に正規分布$N(\mu,\sigma^2)$に従うとき、自由度$k$のカイ二乗分布に従う。
\sum_{i=1}^{k}\left(\frac{X_{i}-\mu}{\sigma}\right)^{2} \sim \chi^{2}(k)\\
自由度k-1のカイ二乗分布に従う場合 \sum_{i=1}^{k}\left(\frac{X_{i}-\bar{X}}{\sigma}\right)^{2}=\frac{(k-1) S^{2}}{\sigma^{2}} \sim \chi^{2}(k-1)
カイ二乗分布と指数分布の関係
自由度2のカイ二乗分布は$λ=\frac{1}{2}$の指数分布と一致する。
f(x ; 2)=\frac{1}{2^{\frac{2}{2}} \Gamma\left(\frac{2}{2}\right)} e^{-\frac{x}{2}} x^{\frac{2}{2}-1}=\frac{1}{2 \times \Gamma(1)} e^{-\frac{x}{2}}=\frac{1}{2} e^{-\frac{x}{2}}
カイ二乗分布のパーセント点

F分布
自由度が$K_1、K_2$のカイ二乗分布$\chi_1\sim\chi^{2}(k_1)、\chi_2\sim\chi^{2}(k_2)$が互いに独立である場合に、
次の式から算出されるFが従う確率分布のこと。
Fは自由度$(K_1,K_2)$のF分布に従う。
F=\frac{\chi_{1}^{2} / k_{1}}{\chi_{2}^{2} / k_{2}}\\
\begin{array}{c}
期待値 E(X)=\frac{n}{n-2} \quad(n>2) \\
分散 V(X)=\frac{2 n^{2}(m+n-2)}{m(n-2)^{2}(n-4)} \quad(n>4)
\end{array}
t分布とF分布の関係
自由度1のカイ二乗分布は標準正規分布に従う確率変数を2乗したものに等しくなるので、
$t$が自由度$n$のt分布に従うとき、$t^2$は自由度$(1, n)$のF分布に従う。
t=\frac{Z}{\sqrt{\frac{W}{n}}}\\
両辺を2乗 t^{2}=\frac{Z^{2}}{\frac{W}{n}}
F分布の2.5パーセント点
2変数の確率分布(同時確率分布)
離散型同時確率分布
同時確率関数
f\left(x_{i}, y_{j}\right)=P\left(X=x_{i}, Y=y_{j}\right) \quad(i=1,2, \cdots ; j=1,2, \cdots)\\
\sum_{i} \sum_{j} f\left(x_{i}, y_{j}\right)=1\\
周辺確率関数
ある1つの確率変数を抜き出してその確率の総和を求めたもの。
\begin{array}{ll}
f_{x}\left(x_{i}\right)=\sum_{j} f\left(x_{i}, y_{j}\right)=P\left(X=x_{i}\right) & (i=1,2, \cdots) \\
f_{y}\left(y_{j}\right)=\sum_{i} f\left(x_{i}, y_{j}\right)=P\left(X=y_{j}\right) & (j=1,2, \cdots)
\end{array}
連続型同時確率分布
同時確率密度関数
P(a \leq X \leq b, c \leq Y \leq d)=\int_{a}^{b} \int_{c}^{d} f(x, y) d x d y\\
\int_{-\infty}^{\infty} \int_{-\infty}^{\infty} f(x, y) d x d y=1
周辺確率密度関数
\begin{array}{l}
f_{x}(x)=\int_{-\infty}^{\infty} f(x, y) d y \\
f_{y}(y)=\int_{-\infty}^{\infty} f(x, y) d x
\end{array}
期待値
\begin{array}{l}
E(X+Y)=E(X)+E(Y) \\
E(X-Y)=E(X)-E(Y)
\end{array}\\
XとYが独立である場合 E(X Y)=E(X) E(Y)
分散
\begin{array}{l}
V(X+Y)=V(X)+V(Y)+2 \operatorname{Cov}(X, Y) \\
V(X-Y)=V(X)+V(Y)-2 \operatorname{Cov}(X, Y)
\end{array}\\
共分散が0、すなわちXとYが独立である場合
\begin{array}{l}
V(X+Y)=V(X)+V(Y) \\
V(X-Y)=V(X)+V(Y)
\end{array}
共分散
共分散とは2変数の関係の強さを表す指標。
\operatorname{Cov}(X, Y)=E\left[\left(X-\mu_{x}\right)\left(Y-\mu_{y}\right)\right]\\
\begin{aligned}
上式を展開 \operatorname{Cov}(X, Y) &=E\left[\left(X-\mu_{x}\right)\left(Y-\mu_{y}\right)\right] \\
&=E\left(X Y-\mu_{x} Y-\mu_{y} X+\mu_{x} \mu_{y}\right) \\
&=E(X Y)-\mu_{x} E(Y)-\mu_{y} E(X)+\mu_{x} \mu_{y} \\
&=E(X Y)-\mu_{x} \mu_{y}-\mu_{x} \mu_{y}+\mu_{x} \mu_{y} \\
&=E(X Y)-\mu_{x} \mu_{y}
\end{aligned}
相関係数
$X$と$Y$の共分散$\operatorname{Cov}(X,Y)$をそれぞれの標準偏差で割ったもの。
\rho=\frac{\operatorname{Cov}(X, Y)}{\sqrt{V(X) V(Y)}}
補足:高校数学
シグマ
シグマは和の記号で、シグマの右側にある数値を
一定の条件の下で足し合わせることを表します。
「一定の条件」は、シグマの下側と上側についてる文字で指定する。
$i$の範囲がすでに決められている場合には、下に示したようにシグマの上下に
$a$や$b$の値がでてこない表記をすることがあります。
これは「考えている全ての範囲の$i$について$Xi$を足し合わせる」という意味。
\sum_{i=a}^{b}Xi\\
\sum_{i}Xi\\
微分f(x)
接線の傾きを求める方法で導関数を求めること。
y=x^{n} → f'(x)=nx^{n-1}\\
y=kx^{n} → f'(x)=k×nx^{n-1}\\
積分F(x)
ある領域の面積を求める方法で原始関数を求めること。
y=x^{n} → \int_{a}^{b}x^ndx=\begin{bmatrix}\frac{1}{n+1}x^{n+1}\end{bmatrix}_{a}^{b}\\
y=kx^{n} → \int_{a}^{b}kf(x)dx=k×\int_{a}^{b}f(x)dx\\