Tom Schaul, John Quan, Ioannis Antonoglou, David Silver
ICLR 2016
arXiv, pdf
どんなもの?
深層強化学習を安定して行うためのテクニックにExperience Replayがある.
この論文では,保存したExperienceに優先順位をつけてサンプリングを行うことで,深層強化学習の性能の向上を目指す.
先行研究との差分
深層強化学習に有効な,保存したExperienceへの優先順位の与え方,サンプリング方法を提案した.
技術や手法のキモ
Prioritizing with TD-error
遷移によってどれだけ学習できたか,というのは直接求められないため,TD誤差を用いる.
このTD誤差の大きさは,その遷移がどれだけの「驚き」や「予想外」をもたらすかを表している.
Greedy TD-error priorization
replay memoryに保存された遷移のうち,TD誤差の絶対値が最大のものをリプレイする.
しかしながら,greedy TD-error priorizationには3つの問題点がある.
- リプレイされた行動のTD誤差のみが更新される.そのため,初めにTD誤差が小さかった場合は長期間リプレイされないままになる点
- スパイクノイズにセンシティブである点
- TD誤差の大きな遷移が頻繁にリプレイされてしまう.そのため,多様性が乏しく,過学習を起こしてしまう
Stochastic sampling method
これを克服するため,遷移$i$のサンプリング確率を以下のように定義する.
P(i) = \frac{{p_{i}}^{\alpha}}{\Sigma_{k}{p_{k}}^{\alpha}}
$p_{i} > 0$は遷移$i$の優先度,$\alpha$はどれだけ「優先度」に重きを置くかを表すハイパーパラメータ.
$\alpha = 0$で一様な場合と同じ.
以下の2種類を提案している.
Proportional prioritization (direct)
p_{i} = |\delta_{i}| + \epsilon
$\epsilon$は小さい正の定数で,TD誤差が0であった場合に,サンプリングされなくなるのを防ぐ.
Rank-based prioritization (indirect)
p_{i} = \frac{1}{rank(i)}
$rank(i)$はreplay memoryがTD誤差によってソートされたときの遷移$i$の順位.
このとき,
P(i) = \frac{\Bigl(\frac{1}{rank(i)}\Bigr)^\alpha}{\Sigma_{k}\Bigl(\frac{1}{rank(k)}\Bigr)^\alpha}
と,$\alpha$のべき乗則分布になる.(?)
direct,indirectどちらの分布もTD誤差の絶対値に対して単調だが,後者は外れ値に対してinsensitiveなのでよりロバストらしい.
(?)実装の際のサンプリングについて書かれていたがいまいち理解できていない.
Annealing the bias
Prioritized replayにはuncontrolled fashionによって,異なるサンプリングの分布に収束させてしまうようなbiasが掛かってしまう.
このbiasを修正するためにimportance-sampling (IS) weightを使用する.
w_{i} = \Bigl(\frac{1}{N} \cdot \frac{1}{P(i)}\Bigr)^{\beta}
$\beta = 1$でfully compensate.
Q-learningの更新の際の重み付けには,$\delta_{i}$の代わりに$w_{i}\delta_{i}$を用いる.
安定のため,重みは$\frac{1}{\max_i{w_{i}}}$で正規化する.
$\beta$の値は学習の終了時に1になるように,例えば$\beta_{0}$から1まで線形にスケジューリングする.
以下は,Double DQNにPrioritized Experience Replayを用いる際のアルゴリズム.
どうやって有効性を検証したか
57種類のAtari gamesのスコアで比較.
2つのハイパーパラメータ$\alpha, \beta_{0}$はあらかじめ8つのゲームを使って決定.
$\alpha=0.7, \beta_{0}=0.5$ for the rank-based variant, $\alpha=0.6, \beta_{0}=0.4$ for the proportional variant.
$\alpha, \beta_{0}$は,アグレッシブさとロバストさのトレードオフの関係にある.
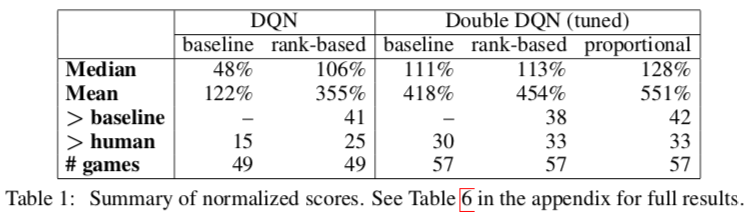
上の表はDQN,Double DQNに適用した結果.
$>$baselineはベースラインのスコアを上回ったゲーム数.
DQN+rank-basedで大幅な向上.
Double DQNにおいても向上が見られた.
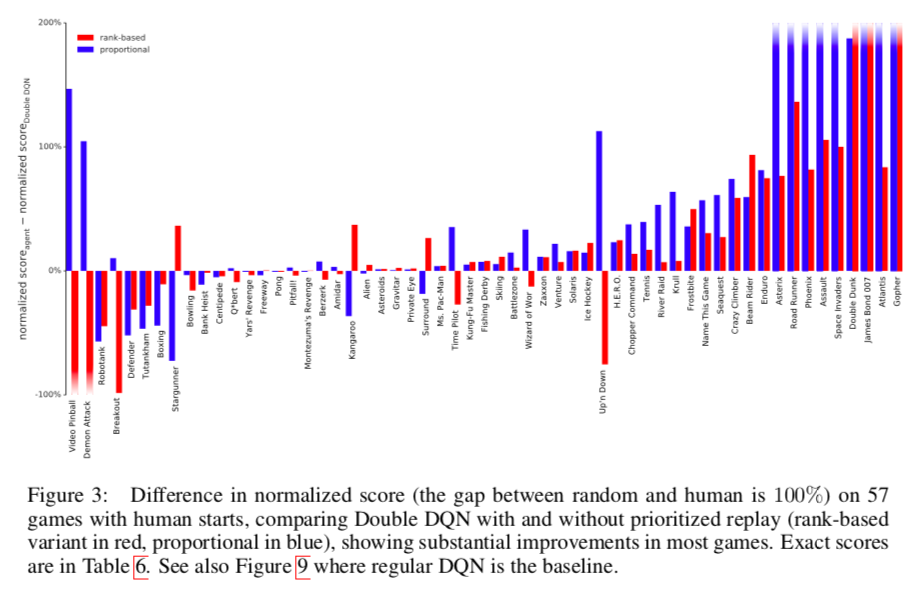
上のグラフはDouble DQNにPrioritized replayを加えた際のnormalized scoreの変化を表している(スコアの100%はrandomとhumanの差に相当).
横軸がゲームの種類,縦軸がnormalized scoreの差.
青がrank-based,赤がproportionalの場合.
だいたいのゲームで向上が見られた.
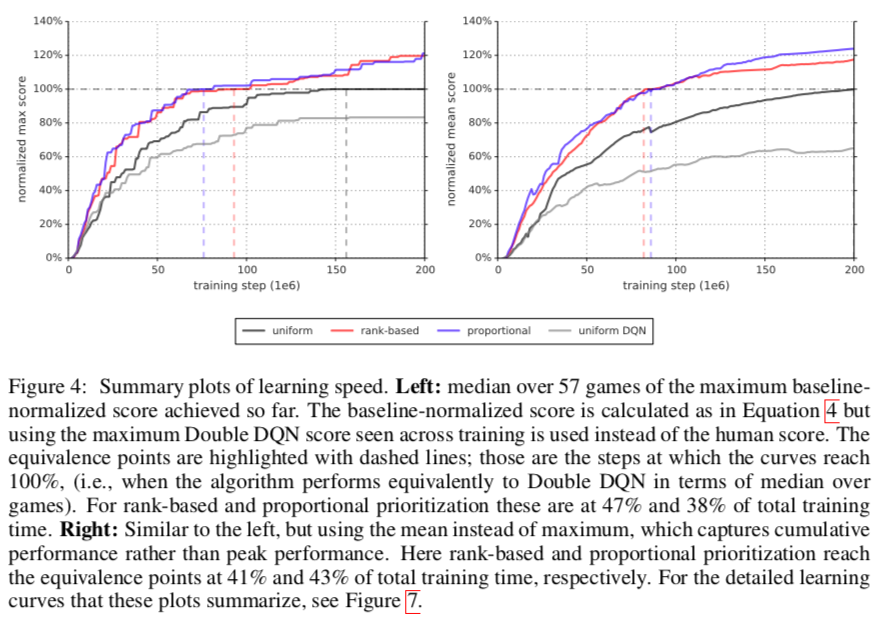
上のグラフは横軸がstep,縦軸がnormalized score(左がmax score,右がmean score).
黑uniform(Double DQN),赤rank-based,青proportional,灰uniformDQN
スコアが100%に到達したステップ数を比較すると,Prioritized replayを加えた方が学習が非常に効率良く進んでいることが分かる.
議論はあるか
- rank-basedの方が外れ値の影響を受けないためロバストだと思っていたが,エラーのスケールがrankに隠れてしまい,パフォーマンスが落ちる場合があった(in sparse reward scenarios).
- どちらのvariantsにおいても実際は,DQNのにおけるrewardsとTD誤差のclippingによって外れ値が除かれているのでは(そのせいでproportionalの方が良かった?) .
- いくつかの遷移の記録はリプレイされないまま捨てられ,多くの遷移は記録されてからずいぶん経ってからリプレイされる.Prioritized replayはこれらの問題を解決する.