参考: 安川章, 「できる人が使っている最小二乗法の一発フィット」,『Interface(インターフェース)』2017年 08 月号(CQ出版), p.143
擬似逆行列を使って求める方法が参考記事に紹介されているのでグラフ電卓 TI-Nspire で再現してみる。
何かを測定して次のデータ対が得られたとする。このデータが N 次函数で近似できるものと假定する。
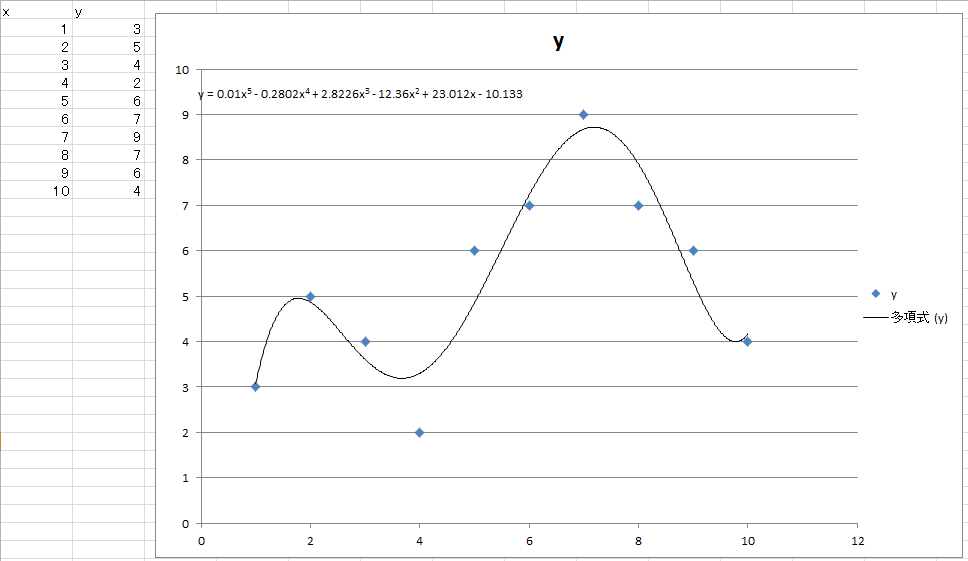
x = {1,2,3,4,5,6,7,8,9,10}
y = {3,5,4,2,6,7,9,7,6,4}
このデータを次のように行列で表現する。
a = [ [x[0]^N, x[0]^(N-1), ......, x[0]^0],
[x[1]^N, x[1]^(N-1), ......, x[1]^0],
.
.
.
[x[k]^N, x[k]^(N-1), ......, x[k]^0] ]
b = [ [y[0]], [y[1]], ......, [y[k]] ]
coeffs = [ [coeffs[N]], [coeffs[N-1]], ......, [coeffs[0]] ]
a * coeffs = b
未知数 coeffs = b * (a^-1) が N 次近似函数の各次数の係数である。
一般にデータのほうが未知数よりも圧倒的に多いため行列 a は正方行列にはならず逆行列 (a^-1) が求まらない。そこで逆行列の代わりに擬似逆行列を利用する。理窟はわからないがこれで最小二乗法と同じ結果になるとの由。擬似逆行列は次式で求まる。
a の擬似逆行列 = ((a の転置行列) * a)^-1 * (a の転置行列)
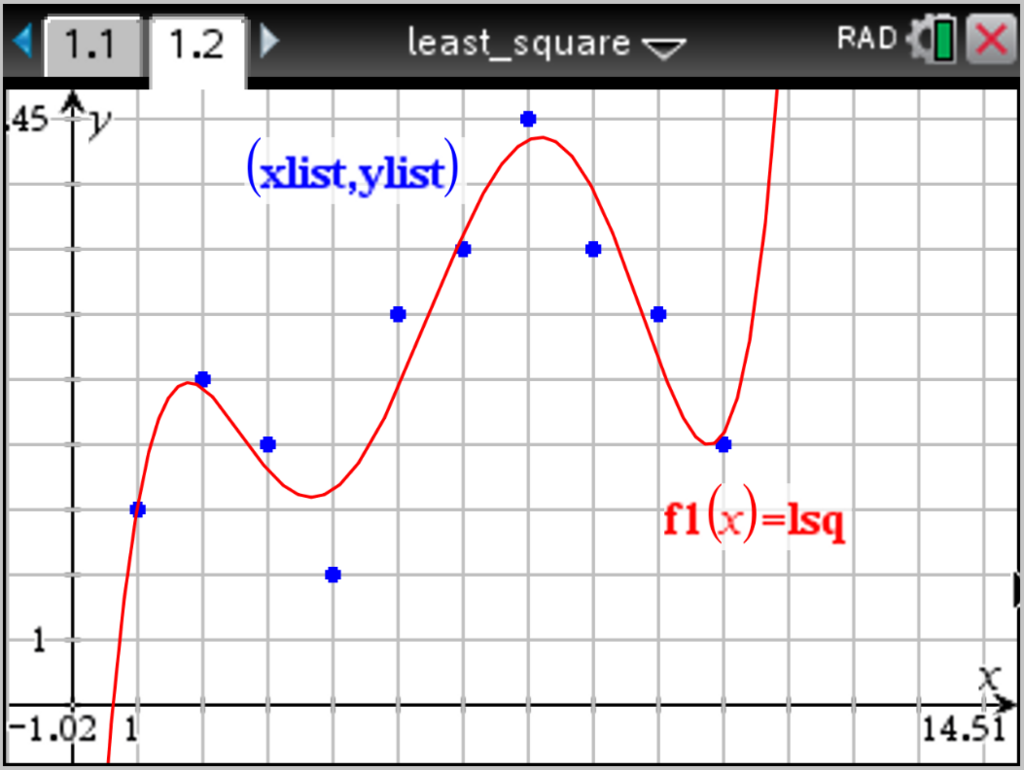
グラフ電卓 TI-Nspire (TI Basic) で組んだプログラム:
(.tns ファイル: https://drive.google.com/open?id=1sTE-hB8h4cQ_xC7vn_EQP2B7nA0pxvZC)
Define least_square(xlist, ylist, order)=
Func
:Local a, a_trans, a_pinv, coeffs, poly_func
:a:= seq(seq(xlist[m]^(n), n, order, 0, −1), m, 1, dim(xlist)) © 行列 a を組み立てる。
:a_trans:= a@t © 行列 a の転置行列を求める。
:a_pinv:= (a_trans * a)^(−1) * a_trans © 行列 a の擬似逆行列を求める。
:b:= (list▶mat(ylist))@t © 行列 b を組み立てる。
:coeffs:= a_pinv * b © 擬似逆行列を使って多項式の各次数の係数を求める。
:coeffs:= mat▶list(coeffs)
:poly_func:= polyEval(coeffs, x) © 近似多項式を組み立てて、
:Return approx(poly_func) © 返す。
:EndFunc
実行結果 (5 次函数で近似してみた):
`(見る/隠す) 3 次までなら回帰分析用の函数が用意されているのでそれを使ったほうが早い`
今回作った least_square() 函数と同じ結果が得られる。
1 次の場合:
2 次の場合:
3 次の場合:
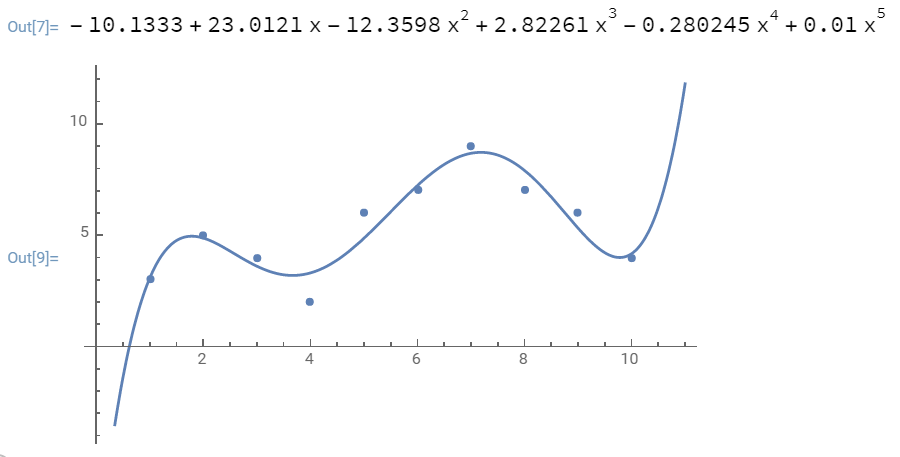
`(見る/隠す) Wolfram の場合 (Fit[] 函数を使う)`
Wolfram の場合は Fit[] 函数で近似多項式が求まる。
構文: Fit[{{x1, y1}, {x2, y2}, ......, {xn, yn}}, {x^0, x^1, ......, x^n }, x]
返値: 多項式
xList = {1,2,3,4,5,6,7,8,9,10};
yList = {3,5,4,2,6,7,9,7,6,4};
order = 5;
xyList = Transpose[{xList, yList}]; (* {{x1, y1}, {x2, y2}, ...} に変換する *)
scatPlt = ListPlot[xyList]; (* 点列の散布図 *)
n = Table[x^n, {n, 0, order}];
polyEq = Fit[xyList, n, x] (* 近似多項式を求める *)
polyPlt = Plot[polyEq, {x, 0, 11}]; (* 近似多項式のグラフ *)
Show[polyPlt, scatPlt] (* 点列の散布図と近似多項式のグラフとを一緒に描く *)
実行結果:
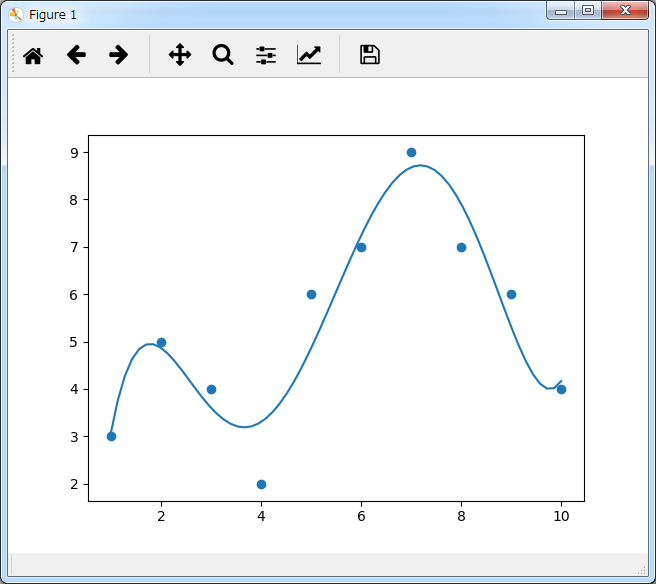
`(見る/隠す) Python の場合 (numpy.polyfit() 函数を使う)`
Python の場合は numpy.polyfit() を使えば簡単に近似多項式が求まる。
構文: numpy.polyfit([x 軸の点列], [y 軸の点列], 次数)
返値: N 次 ～ 0 次の順番に係数の並んだリスト
.py3
import matplotlib.pyplot as plt
import numpy as np
import sympy as sym
x = sym.Symbol("x")
xList = np.array([1,2,3,4,5,6,7,8,9,10])
yList = np.array([3,5,4,2,6,7,9,7,6,4])
N = 5
coeffs = np.polyfit(xList, yList, N)
print("%s ～ 0 次の係数: %s" % (N, coeffs))
eq = np.poly1d(coeffs)
print("近似多項式: %s" % (sym.expand(eq(x))))
x_numbers = np.linspace(xList[0], xList[-1], 2**6+1)
plt.scatter(xList, yList)
plt.plot(x_numbers, eq(x_numbers))
plt.show()
実行結果:
5 ～ 0 次の係数: [ 1.00000000e-02 -2.80244755e-01 2.82261072e+00 -1.23598485e+01 2.30121445e+01 -1.01333333e+01]
近似多項式: 0.0100000000000009*x**5 - 0.280244755244777*x**4 + 2.82261072261092*x**3 - 12.3598484848493*x**2 + 23.0121445221459*x - 10.1333333333339
`(見る/隠す) Excel の場合 ([近似曲線の追加]を使う)`
Excel の場合は表計算をする必要すらない。まず散布図を描いてから、グラフ上のどれか要素を右クリックし、[近似曲線の追加]、[多項式近似] の順に選択し、[次数] ボックスで次数を指定すれば多項式近似曲線が描かれる。[グラフに数式を表示する] チェックボックスをオンにすると数式も一緒に表示される。
実行結果:
