この記事は 機械学習の数理 Advent Calendar 2018 の 11 日目のための記事です. 間に合いましたか?
この記事について
McInnes らによる "Uniform Manifold Approximation and Projection (UMAP)" を読み, その解説を試みます.
UMAP は t-SNE のようにデータの次元削減とその可視化を提供する手法です.
t-SNE よりも可視化の結果がより良く見える (同じクラスタはよりまとまっている) ことや, データを fuzzy topology というこれまで使われてこなかったけど数学的裏付けがあってイケてる方法で表現したぜ! と言ってる点が目を引き, 読んでみようと思ったのですが, 圏論の言葉で書かれており読むのに苦労していたら12月になっていました.
機械学習界隈で圏論に馴染みがあることを仮定するのは無理があると思うので, 圏論の言葉を極力使わずに説明を試みたいと思います. (そのためにいくつか誤魔化しがあります.)
リンク
論文と著者による実装は以下にあります.
- arxiv:1802.03426
-
github:lmcinnes/umap
-
pip install umap-learnでいけます (NOTE:-learnを忘れずに)
-
その他に以下を参考にしました.
-
kaggle - Dimensionality reduction with UMAP on MNIST
- UMAP の使い方を説明してくれるチュートリアルとして読めます.
-
nLab - simplicial set
- simplicial set (単体的集合) の解説です. Wikipedia より図がちゃんと載ってて良い.
概要
Uniform Manifold Approximation and Projection (UMAP) は t-SNE と同様に, 与えられた点列について次元削減 (次元圧縮) を行って 2, 3 次元ユークリッド空間に写すことで, 可視化を行ってくれるようなツールです. kaggle - Dimensionality reduction with UMAP on MNIST にもあるように, MNIST における画像データをそのまま 28x28 次元ユークリッド空間の点だと思って UMAP を適用するだけで, かなり良いクラスタリングが為されたような二次元の点に写されていることが観察できます.
ちなみに私もMNISTの画像 10,000 枚で試してみました. プロットの色がラベルに相当します. UMAP と t-SNE で比較しています. 正直, t-SNE は遅すぎてパラメータ調整が嫌になりますね.
| Method | Result | Time |
|---|---|---|
| UMAP |  |
CPU times: user 27.9 s, sys: 412 ms, total: 28.3 s |
| t-SNE |  |
CPU times: user 4min 23s, sys: 556 ms, total: 4min 24s |
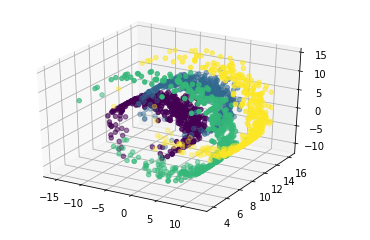
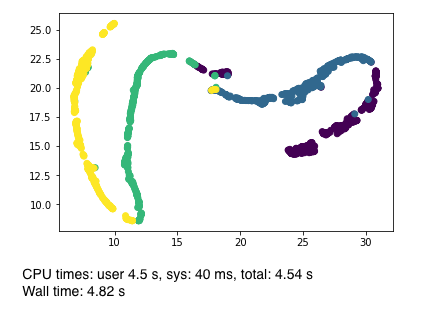
もののついでなので, この手のダミーデータとしてよく使われる Swissroll についても試してみました.
手法は大きく3つのフェーズから成ります.
- リーマン多様体 (~ 距離空間) の推定
- 観察されるデータはこの多様体の上に一様分布しているものだと仮定する
- タイトル回収
- 距離空間の fuzzy topological 表現
- ここが論文のメインではあるのですが...
- 次元削減の方法
- ここでは元のデータを fuzzy topology で表現したものと, ターゲットの次元の点列 (例えば二次元) を fuzzy topology で表現したものとを比べて, 2つを近くなるように, ターゲットの点列を動かしていく
- 一応ここで fuzzy topology 表現にしたことの良さがあります
順に見ていきます.
あ、ですます調は疲れるのでここでやめます.
1: リーマン多様体の推定
UMAP の入力は点列である. すなわち, ある自然数 $n$ があって, $$x_1, x_2, \ldots, x_N \in \mathbb R^n$$ が与えられる.
ここで $\mathbb R^n$ は $n$ 次元ユークリッド空間.
UMAPの第1フェーズは多様体学習を行う.
すなわち, データ $x_i$ は $\mathbb R^n$ の点と見做せるが, 実際にはある図形 $M \subset \mathbb R^n$ があって, $x_i \in M$ の点として観察されると考えるのが自然である.
例えば画像であれば, そもそも $\mathbb R_{\geq 0}^n$ であるし, その中でもランダムノイズのようなものを考慮しないなら, そのようなものはデータ空間から除外したい (場合によるけど).
となるともちろん, $M$ の距離はユークリッド距離であるのは不自然で, 一般に $M$ はリーマン多様体であるとしておく. $M$ のある部分の点はよく観察される, などの偏りが計量によって表現される. そしてその推定に次のような補題を用いる (これは論文の Lemma 1 を非形式的に (かつ不正確に) 書き直したもの).
補題
点列 $X = \{x_1,\ldots,x_N \in \mathbb R^n \}$ がリーマン多様体 $M \subset \mathbb R^n$ から一様にサンプリングされたものとする. また, $M$ の計量は局所的には単位行列の定数倍で表現されるとする (つまり, ユークリッド空間を定数倍しただけの空間とみなせることを仮定している).
このとき, 各点 $x_i$ を中心に ($M$ の計量で) 半径 $1$ の球をとったとき, 球の内部に含まれる $X$ の点の個数は, その中心の点 $x_i$ に依らず一定である.
これを用いれば次のことが言える.
したがって, 逆に定数 $k (<N)$ というもの決めておいて, $x_i$ を中心に $k$ 個の点をギリギリ含むような, ユークリッド空間の中の球を描いたとき, その半径を $x_i$ の周りの計量での距離 $1$ として定めればよい.
この方法で定まる距離を $d_M$ と書くことにする.
Extended-Pseudo-Metric Space
今のうちにこの論文の議論の中で用いる距離空間について定義しておく.
ここでは通常の距離をさらに緩めた EPMet (Extended-Paused-Metric) を用いる.
EPMet $(X,d)$ は次の3つを公理とする関数
$$d : X \times X \to \mathbb R_{\geq 0} \cup \{ \infty \}$$
のこと.
- $d(x,y) \geq 0$ and $d(x,x)=0$
- $d(x,y) = d(y,x)$
- $d(x,z) \leq d(x, y) + d(y,z)$
注意として, 無限の距離を許すことと, 異なる二点間の距離がゼロであることを許すこと.
もちろん $(M, d_M)$ は EPMet になっている.
さらに $X$ が有限空間の場合の EPMet を FinEPMet と呼ぶことにする.
入力の点列だけからなる空間のことを考える場合はこちらを用いることになる.
2: 距離空間の fuzzy topological 表現
ここがこの論文のメインである. けど別に理解しなくてもUMAPは説明できるし実装できるとかいうね
Fuzzy topology は昔あったファジー理論を複体に取り入れたようなもの (これで説明終わってもいいんじゃない?).
(ちょうど今の "AI" という言葉と同じように "ファジー制御" という言葉がありとあらゆる家電やビジネスシーンに取り入れられたことがあるという話を伝え聞いたことがあります.)
散々言ったところでせっかく読んだので説明します.
話の流れ
次の概念を順に導入していきます.
- fuzzy set
- ファジーな集合
- simplicial set
- 複体のこと
- fuzzy simplicial set
- 1 と 2 の組み合わせ
- FinReal
- 単体を EPMet に変換する
- FinSing
- EPMet を fuzzy simplicial set に変換する
fuzzy set
集合というもののデータ構造について考える.
集合 $X$ があるとき, 自由にとってきた数 $x$ について $$x \in X$$ または $$x \not\in X$$ を判定することが集合というデータには求められる.
値が属するかどうかを判定する述語はよくメンバーシップ関数と呼ばれる.
すなわち, 集合 $X$ について, 次のような関数 $\mu_X$ のことを $X$ のメンバーシップ関数と言う.
$$\mu_X(x) = \begin{cases}
1 & \text{ when } x \in X \\
0 & \text{ otherwise }
\end{cases}$$
便宜的にありえる数 $x$ の全体を $\mathrm{Any}$ という集合だとしておくと $$\mu_X \colon \mathrm{Any} \to \{0,1\}$$ である.
逆に, メンバーシップ関数 $\mu$ があるときに, 集合自体は $\mu(x)=1$ なる $x$ を全て集めてきたもの, として構成することができる.
$$X = \{ x \in \mathrm{Any} \mid \mu(x) = 1 \}$$なので集合 $X$ と書く代わりに集合 $\mu$ と書いても問題ない (台となる $\mathrm{Any}$ が明らかな場合).
さて fuzzy set はメンバーシップ関数の値を緩めたもので, そのメンバーシップ関数は数を受け取ったら $[0,1]$ の実数を返す.
$$\mu \colon \mathrm{Any} \to [0,1]$$その値は "membership strength" と呼ばれ, $0$ であるほど集合に属して無くて, $1$ であるほど集合に属している. 属する確率だと思ってもいいかもしれない.
メンバーシップ関数 $\mu$ ととり得る値の全体 $A$ (あるいは $\mathrm{Any}$) によって, $(A, \mu)$ を fuzzy set と呼ぶ. あるいは $A$ が明らかな場合, 単に fuzzy set $\mu$ と書くことにする.
集合のときと同様に, メンバーシップ関数 $\mu$ から集合の形にすることを考える. fuzzy set 自体は実数を受け取ったら, その値以上の strength で属する値全てを集めてきたものであるとする.
$$X \colon [0,1] \to \mathrm{Sets}$$ $$X(a) = \{ x \in \mathrm{Any} \mid \mu(x) \geq a \}$$
したがって, $a \leq b$ について, $X(a) \supseteq X(b)$ という関係がある.
このような関数 $X$ のこともまた fuzzy set と呼ぶ.
simplicial set
正確な定義は nLab - simplicial set を参照のこと.
Definition 2.2 にある図を眺めるだけでも, なんとなくわかりそう.
simplicial set は単体的複体を圏論的に定義し直したもの.
ここでは簡単に単体的複体 $X$ について, その $n$ 次元以下の部分複体を集めてきた集合を $X_n$ として与えるようなものを, simplicial set $X$ と定義する.
例えば $X_0$ は $X$ が持つ頂点だけを集めたもの. $X_1$ は $X_0$ に辺を加えたもの.
あ、ところでこの論文はたぶん $n$ を $1$ スタートにして $X_1$ が頂点だとしてる.
この記事では $0$ スタートにします (nLab がそうなのでこっちが一般的だと思うことにする).
fuzzy simplicial set
simplicial set $X$ は, 各 $n$ について集合 $X_n$ を与えるものであった.
この集合を fuzzy set にしたのが fuzzy simplicial set である.
簡単.
例えば fuzzy simplicial set $X$ があるときに, これが strength $a$ 以上で持つ $n$ 次元以下部分単体を集めた集合を $X^n_a = X^n(a)$ と書くことにする.
$X^n$ のメンバーシップ関数を $\nu^n$ とすれば, $$X^n_a = \{ \sigma \in \Delta^0 \cup \cdots \cup \Delta^n \mid \nu^n(\sigma) \geq a \}$$ と書ける.
ここで $\Delta^m$ は $m$-単体全体のこと.
FinReal
EPMet (FinEPMet) の話と fuzzy simplicial set の話をしたので, この2つの間の変換の話をする. ただしここからはだいぶアドホック.
FinReal は fuzzy な $n$-単体を FinEPMet に変換する (この記事ではそういうことにする).
strength $a \in [0,1]$ で存在する $n$-単体を $\Delta^n_a$ と書くことにすると (論文とは記法の意味が変わってるが),
$$\mathrm{FinReal}(\Delta^n_a) = (\{x_0,x_1,\ldots,x_n\}, d_a)$$
ただしここで
$$d_a(x_i, x_j) = \begin{cases}
-\log(a) & \text{ when } i \ne j \\
0 & \text{ otherwise }
\end{cases}$$
要するに右辺は 1 個の $n$-単体についての EPMet を定めている.
距離空間の台は $n+1$ 点からなる集合で, これは $\Delta^n$ が持つ $n+1$ 個の頂点のこと.
距離は, $a$ が $0 \mapsto 1$ で大きくなるに従って, 無限大から $0$ に向かって小さくなるような関数で定める.
この関数はどこから来たの? と思ってしまうけどね.
FinSing
FinSing は FinEPMet $(Y, d)$ に対して fuzzy simplicial set を与える操作.
つまり $X = \mathrm{FinSing}(Y, d)$ を定める.
ここで $X$ は $n \in \mathbb N$ と $a \in [0,1]$ に対して単体の集合 $X^n_a$ を与えるもので, それは次のように定められる.
$$X^n_a = \{ \overline{f(x_0) \cdots f(x_n)} \mid f \in \mathrm{Hom}(\mathrm{FinReal}(\Delta^n_a), Y) \}$$
ここで, まず $\mathrm{Hom}(A,B)$ は 2つの EPMet $(A,d_a)$ と $(B,d_b)$ について, $$f \colon A \to B$$ なる関数であって, 非拡大的であるようなもの. つまり,
$$\forall x,y \in A, d_b(f(x), f(y)) \leq d_a(x, y)$$
というもの. そういう関数 $f$ を全て集めてきたものを $\mathrm{Hom}(A,B)$ と書く.
ここでは $A=\mathrm{FinReal}(\Delta^n_a)$ であるので, 空間は $\{x_0,x_1,\ldots,x_n\}$ であって距離 $d_a$ も上の FinReal の章で定義したもの.
$f \in \mathrm{Hom}(\mathrm{FinReal}(\Delta^n_a), Y)$ とは, $i=0,1,\ldots,n$ について $f(x_i) \in Y$ を与えるものであって, しかも $$i \ne j \implies d(f(x_i),f(x_j)) \leq -\log(a)$$ なるもののこと.
このような関数 $f$ について $\overline{f(x_0) \cdots f(x_n)}$ というのは (これは私が今作った記号),
$Y$ の $n+1$ 点 ${f(x_0) \cdots f(x_n)}$ を頂点にして結んで出来る $n$ (以下)-単体のこと ($f$ が単射である必要はないので, 点が重複したとき, その単体の次元は $n$ より小さくなる).
以上で FinSing は定義された. $X^n_a$ という形で定義したが, $$\mu(\sigma \in \Delta^n) = \inf \{ a \in [0,1] \mid \sigma \in X^n_a \}$$ としてメンバーシップ関数も構成できる.
FinReal と FinSing のまとめ
FinSing は EPMet を fuzzy simplicial set に変換する.
それには, 十分距離が小さいところは線 (あるいは超面) で結んで複体を作ればいい.
小さいと判定するための距離の上限の閾値を fuzzy が持つ strength によって可変にしてやる.
strength から距離への変換は適当な (例えば対数のマイナス) 関数を噛ませることで実現する.
2.99999. ここまでのまとめと実装
2章が長くなったので一旦ここまでの話を振り返る.
まず1章ではデータ点列からリーマン多様体を推定する方法を述べた.
といっても本当に多様体そのものの形を推定したのではなくて, 有限空間の上の距離 (FinEPMet) を推定してやった.
3章では複体を fuzzy にしたような fuzzy simplicial set を定義し, FinSing という FinEPMet を fuzzy simplicial set に変換するための操作を定義した.
距離の変形
ただし彼らは 1 の方法で推定した FinEPMet を直接 FinSing に与えることはしないで, 少し変形させてから使った.
これは推測だが (あるいは読解不足だが), 彼らの要請として, 推定される複体は1個に連結であることがある. どんな strength でも連結してるとさせるためには距離をゼロにする必要がある. また locally connected であることを要請している. すなわち, 点 $x$ の周りでは $x$ とその近傍だけが繋がっており, その外側は気にしない (一般には繋がっていない). ここで使っている距離空間は無限の距離を許すし, 異なる二点間の距離がゼロであっても良いのであった.
1 で推定した距離を $d_M$ とする. これは実際には各点 $x_i$ の周りで $d(x_i, x_j)$ という形だけで与えられる.
これを用いて次のような関数の族 $\{d_1, d_2, \ldots, d_N\}$ を構成する. ここで $N$ はデータ点の個数.
$$d_i(x_j, x_k) = \begin{cases}
0 & \text{ when } j=k \\
d_M(x_i, x_k) - \rho_i & \text{ when } i=j \\
d_M(x_i, x_j) - \rho_i & \text{ when } i=k \\
\infty & \text{ otherwise }
\end{cases}$$
ただしここで $\rho_i$ は $x_i$ から見て近傍の点までの $d_M$ での距離.
従ってどの点も最近傍との点との距離はゼロ.
また $d_i$ においては $x_i$ 以外同士の距離は無限.
これによって, データ列 $$X = \{x_1, x_2, \ldots, x_N \in \mathbb R^n\}$$ から FinEPMet の族 $$\{ (X,d_i) \}_i$$ が構成される.
このそれぞれを FinSing に与えることで $N$ 個の fuzzy simplicial set が作られる.
これらの和を取ったものを, $X$ の "fuzzy topological representation" と呼ぶ.
$$\bigcup_{i=1}^N \mathrm{FinSing}(X,d_i)$$
和を定義してないので念の為.
2つの fuzzy set $X$ と $Y$ との和とは $$(X \cup Y)(a) = X(a) \cup Y(a)$$ なるもののこと.
メンバーシップ関数の形であれば max を取ればいい.
3: 次元削減の方法
2つの fuzzy set $(A,\mu)$, $(A,\nu)$ の交差エントロピーをよくあるように定義する.
$$C(\mu, \nu) = \sum_{a \in A} \left[ \mu(a) \log \frac{\mu(a)}{\nu(a)} + (1 - \mu(a)) \log \frac{1 - \mu(a)}{1 - \nu(a)} \right]$$
(やっぱ確率じゃん)
これによって2つの fuzzy topological 表現どうしの距離のようなものを定義できたことにもなる.
(単体の次元 $n$ をどうするかが分からないんだけど, 実装だと辺までしか見てないからそもそも $n=1$ にしか気にしていない.)
この $C$ を目的関数にすることで次元削減が出来る.
すなわち, 入力 $X = \{x_1, x_2, \ldots, x_N \in \mathbb R^n\}$ に対して, 目的の低い次元の空間に $N$ 個の点 $Y = \{y_1, y_2, \ldots, y_N \in \mathbb R^m; m \ll n \}$ を用意する.
$m$ は $2$ とか $3$ とか.
$Y$ には普通のユークリッド距離 $d_E$ を入れる.
2つの topological 表現の $C$ を近くなるように $(Y,d_E)$ を SGD などで更新する.
$C$ は $\mu=\nu$ のときに最小値 $0$ を取って, このときは $X$ における推定された距離 $d(x_i, x_j)$ と $d_E(y_i,y_j)$ とが等しくなるようになっている.
これによって得た $Y$ をプロットすることで, 結局 $M$ において近くにある点が視覚的にも近い点としてプロットされるようになる. t-SNE のように局所的な接続関係が保たれて可視化される.
まとめ
- データ (でかいユークリッド空間の点の列) $\to$ fuzzy topological 表現 $X$
- 小さい (2,3次元ユークリッド) 空間の点の列 $\to$ $Y$
- $C(X,Y)$ を最小化する
感想
FinReal の一個前までは良かったのに, 急に FinReal という泥臭い操作が出てきて残念だった. 全体のストーリーは面白かったけど.
というかぶっちゃけ fuzzy topological 表現にしなくても EPMet 同士で交差エントロピー測ればいいんじゃ...
Fuzzy topology という理論をどうしても使いたかっただけにしか見えない.
それから実際の実装を見ると, 結局, 辺 (1-単体) しか考えてない.
これで十分ということなんだろうけど.
その場合は点対だけを考えればよくて, しかも各点について $K$ 近傍まで見ればいいだけなので, 点の数 $N$ だとして全体で $NK$ だけチェックすれば一回の更新が出来る.
それ以外にも, ある程度良い初期値を $Y$ に使うなど他にも工夫をしてるようで, t-SNE に比べて超高速なので実用性も高い.
結果も悪くなることはまず無いのでとりあえず使っておけばいいと思う.
t-SNEより良い視覚化が出来ると言ってるのでその考察も欲しかった.
最後に
圏論の言葉を使わないように説明を試みたので FinReal 辺りから誤魔化しが激しくなった感じがあります.
正確なのは cympfh.cc/paper/UMAP.html に書いておきました.
追記
なんか2日前に論文がめっちゃアップデートしとるな(説明が丁寧になってるぽい)
An updated and significantly expanded version of our UMAP paper is now on arXiv: https://t.co/bq4WuzuXvB
— Leland McInnes (@leland_mcinnes) December 8, 2018
More explanation, algorithm descriptions, and more experiments looking at stability, and working directly on high dimensional data -- as high as 1.8 million dimensional data! pic.twitter.com/Frsqwj7GmP