テーマ
以前投稿した「FPGAでハードウェアアクセラレータを作る:①ワークメモリを作る」の続きです。
今回は”シグモイド関数”を演算する回路を作成します。
シグモイド関数とは
シグモイド関数は、ディープラーニングの分野でも度々登場する関数です。
詳しい説明はネット上にたくさんありますので、省略します。
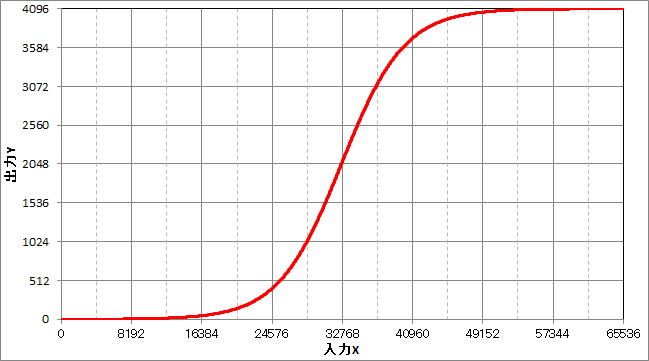
回路をブラックボックスと考えた場合、
__入力Xを入れた時の出力応答Y__が下図のような特性となるモジュールと考えることができます。
回路仕様
- 入力X : 16bit
- 出力Y : 12bit
- 最大勾配1以下(ΔY/ΔX <= 1)
※今回はカーブを再現するだけなのでストレートバイナリで考えています
※使用するアプリケーションが決まった場合は、出力Yを2の補数(固定小数)に変換することを想定しています。
実装方式
シグモイド関数は、RTLで実装するにはかなり難易度が高い為、__"LUT参照法"__を用いて回路実装を行うこととします。
LUT参照法とは?
関数の入出力特性表を予め作成しておきROMに記録しておきます。
- ROMのアドレスを関数の入力
- ROMの出力を関数の出力
とすることで、X/Y特性を実現できます。
- メリット
- 複雑な演算回路を組まなくてもよい
- シグモイド関数に限らず、どんな関数でも実現しやすい(ガンマ変換などでも使われているらしいです)
- デメリット
- ROMに収まる範囲でしかbit数を増やせない
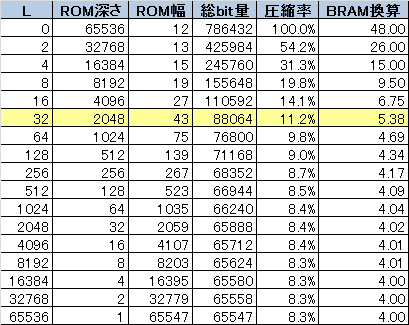
必要なROM容量
まず、出力のが12bitなのでROMのデータ幅が12bitになります。
入力が16bit(65536通り)ありますので深さが65536になります。
よって、66,536 × 12bit =>786,432[bit] のROM容量が必要となります。
これを、Spartan-6 FPGAの "BlockRAMで何個分に相当するか" 換算すると、
BRAMは1個あたりが2KByte(=16,384[bit])なので、__48個分__に相当します。
今回使用しているデバイス(XC6SLX45)ではBRAMが116個なので、実装は可能ですが半分近く使用することとなります。。。
ROM容量を削減するテクニック
今回の関数には以下2点の特徴がある為、ROMに記憶させるデータを削減することが可能です。
| No | 特徴 | 説明 |
|---|---|---|
| 1 | dy/dx>0 微分値が0より大きい |
傾きが0以上 (必ず右肩上がり) |
| 2 | dy/dx=<1 微分値が1以下 |
傾きが1以下 (入力が1増加したときに出力が2以上増えることは無い) |
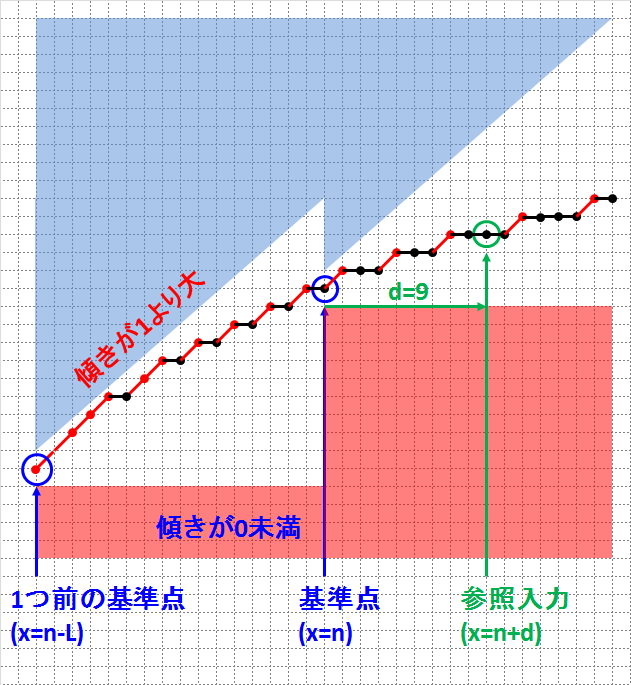
これは、ある基準点から次の基準点までの間に有りえるパターンが下図のように限定されていることを意味します。
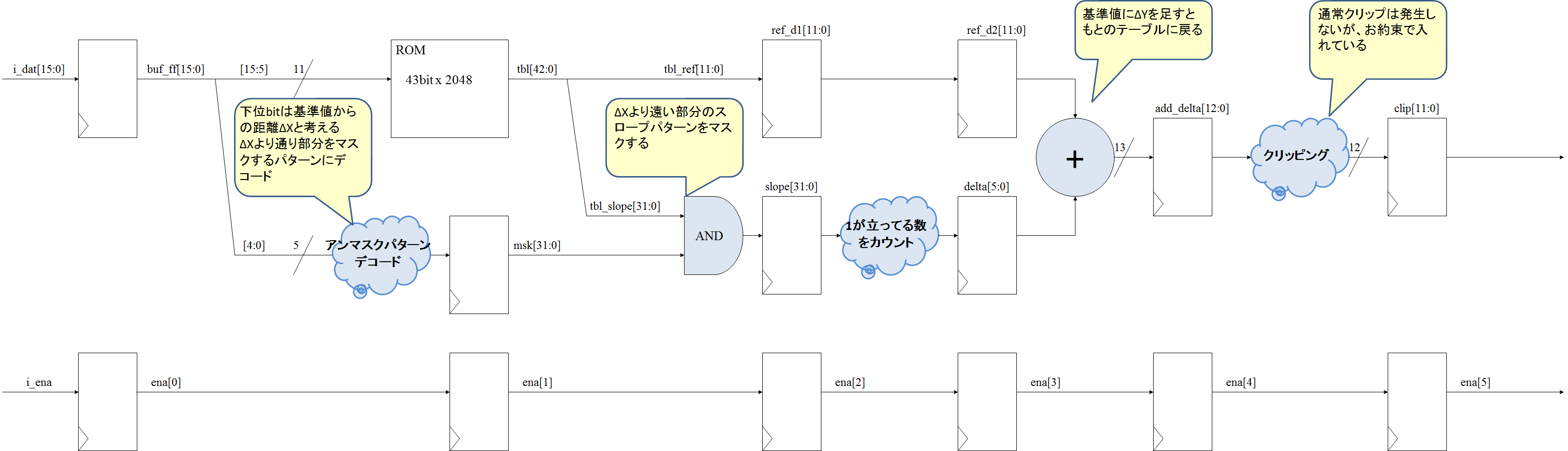
よって、基準点からL個分の出力データを、__"基準値"と"スロープパターン"__の2つの情報に置換えてROMに格納し、回路で復元することでROM要領を圧縮できます。
スロープパターン
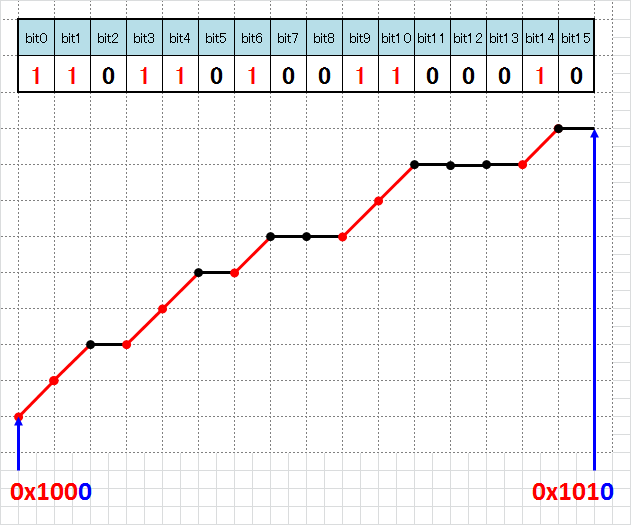
スロープパターンは、以下のルールにしたがって表現することとします。
- 基準点間の距離Lは2のべき乗にする
- スロープパターンをL[bit]で表現する
- 前の値から変化しない場合(黒線)を"0"で表現
- 前の値から増加する場合(赤線)を"1"で表現
- 基準値から近い順にLSB詰めする
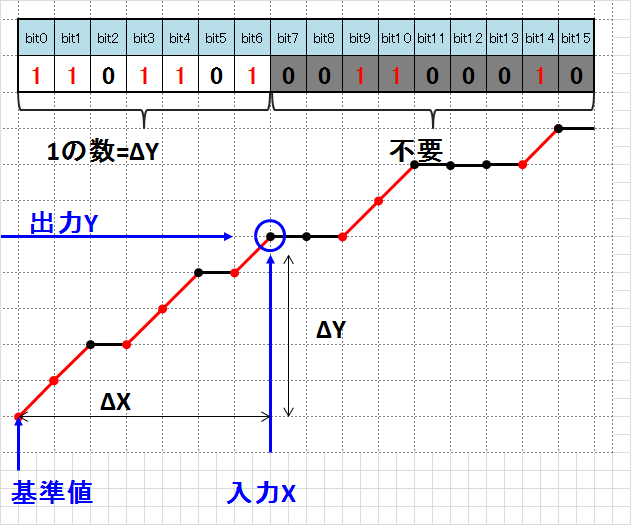
復元方法
入力Xに対応する出力Yを求めるには、基準値にΔYを加算します。
ΔYはスロープパターンから、ΔXより遠い距離にあるbitをマスクして1の立っている数を数えることで求めることが可能です。
圧縮効果
ROM使用量の圧縮効果を下表に示します。
圧縮率を高めるほど、解凍に必要な回路は大きくなりますので、今回はL=32として回路設計しました。
回路
作成したRTLを下図に示します。
パイプラインレイテンシは6サイクルです。
Verilogソースコード
`default_nettype none
module SIGMOID
(input wire i_clk //
,input wire i_ena //
,input wire[15:0] i_dat //
,output wire o_ena //
,output wire[11:0] o_dat //
);
reg[5:0] ena =6'd0 ;
reg[15:0] buf_ff =16'd0 ;
reg[31:0] msk =32'd0 ;
reg[11:0] ref_d1 =12'd0 ;
reg[11:0] ref_d2 =12'd0 ;
reg[31:0] slope =32'd0 ;
reg[5:0] delta =6'd0 ;
reg[12:0] add_delta =13'd0 ;
reg[11:0] clip =12'd0 ;
wire[42:0] tbl ;
wire[11:0] tbl_ref =tbl[11:0] ;
wire[31:0] tbl_slope =tbl[42:12] ;
wire[31:0] nc[0:4];
//=====================================================================
//出力ポート
//=====================================================================
assign o_ena =ena[5];
assign o_dat =clip;
//=====================================================================
//1が立っている数を数える加算器
//=====================================================================
assign nc[0] = {1'b0,slope[31] ,1'b0,slope[29] ,1'b0,slope[27] ,1'b0,slope[25]
,1'b0,slope[23] ,1'b0,slope[21] ,1'b0,slope[19] ,1'b0,slope[17]
,1'b0,slope[15] ,1'b0,slope[13] ,1'b0,slope[11] ,1'b0,slope[9]
,1'b0,slope[7] ,1'b0,slope[5] ,1'b0,slope[3] ,1'b0,slope[1]
}
+ {1'b0,slope[30] ,1'b0,slope[28] ,1'b0,slope[26] ,1'b0,slope[24]
,1'b0,slope[22] ,1'b0,slope[20] ,1'b0,slope[18] ,1'b0,slope[16]
,1'b0,slope[14] ,1'b0,slope[12] ,1'b0,slope[10] ,1'b0,slope[8]
,1'b0,slope[6] ,1'b0,slope[4] ,1'b0,slope[2] ,1'b0,slope[0]
};
assign nc[1] = {2'b00,nc[0][31:30] ,2'b00,nc[0][27:26]
,2'b00,nc[0][23:22] ,2'b00,nc[0][19:18]
,2'b00,nc[0][15:14] ,2'b00,nc[0][11:10]
,2'b00,nc[0][7:6] ,2'b00,nc[0][3:2]
}
+ {2'b00,nc[0][29:28] ,2'b00,nc[0][25:24]
,2'b00,nc[0][21:20] ,2'b00,nc[0][17:16]
,2'b00,nc[0][13:12] ,2'b00,nc[0][9:8]
,2'b00,nc[0][5:4] ,2'b00,nc[0][1:0]
};
assign nc[2] = {4'b0000,nc[1][31:28]
,4'b0000,nc[1][23:20]
,4'b0000,nc[1][15:12]
,4'b0000,nc[1][7:4]
}
+ {4'b0000,nc[1][27:24]
,4'b0000,nc[1][19:16]
,4'b0000,nc[1][11:8]
,4'b0000,nc[1][3:0]
};
assign nc[3] = {8'b00000000,nc[2][31:24]
,8'b00000000,nc[2][15:8]
}
+ {8'b00000000,nc[2][23:16]
,8'b00000000,nc[2][7:0]
};
assign nc[4] = {16'b0000000000000000,nc[3][31:16] }
+ {16'b0000000000000000,nc[3][15:0] };
//=====================================================================
//データイネーブル遅延:パイプラインレイテンシに合わせて遅延
//=====================================================================
always@(posedge i_clk)begin
ena <={ena[4:0],i_ena};
end
//=====================================================================
//演算パイプライン
//=====================================================================
always@(posedge i_clk)begin
//Stage1
//--------------------------------------
//入力バッファFF
buf_ff <=i_dat;
//Stage2
//--------------------------------------
//アンマスクパターンデコード(0:マスク 1:非マスク)
case(buf_ff[4:0])
5'd0 :msk <=32'b0000000000000000000000000000000;
5'd1 :msk <=32'b0000000000000000000000000000001;
5'd2 :msk <=32'b0000000000000000000000000000011;
5'd3 :msk <=32'b0000000000000000000000000000111;
5'd4 :msk <=32'b0000000000000000000000000001111;
5'd5 :msk <=32'b0000000000000000000000000011111;
5'd6 :msk <=32'b0000000000000000000000000111111;
5'd7 :msk <=32'b0000000000000000000000001111111;
5'd8 :msk <=32'b0000000000000000000000011111111;
5'd9 :msk <=32'b0000000000000000000000111111111;
5'd10 :msk <=32'b0000000000000000000001111111111;
5'd11 :msk <=32'b0000000000000000000011111111111;
5'd12 :msk <=32'b0000000000000000000111111111111;
5'd13 :msk <=32'b0000000000000000001111111111111;
5'd14 :msk <=32'b0000000000000000011111111111111;
5'd15 :msk <=32'b0000000000000000111111111111111;
5'd16 :msk <=32'b0000000000000001111111111111111;
5'd17 :msk <=32'b0000000000000011111111111111111;
5'd18 :msk <=32'b0000000000000111111111111111111;
5'd19 :msk <=32'b0000000000001111111111111111111;
5'd20 :msk <=32'b0000000000011111111111111111111;
5'd21 :msk <=32'b0000000000111111111111111111111;
5'd22 :msk <=32'b0000000001111111111111111111111;
5'd23 :msk <=32'b0000000011111111111111111111111;
5'd24 :msk <=32'b0000000111111111111111111111111;
5'd25 :msk <=32'b0000001111111111111111111111111;
5'd26 :msk <=32'b0000011111111111111111111111111;
5'd27 :msk <=32'b0000111111111111111111111111111;
5'd28 :msk <=32'b0001111111111111111111111111111;
5'd29 :msk <=32'b0011111111111111111111111111111;
5'd30 :msk <=32'b0111111111111111111111111111111;
5'd31 :msk <=32'b1111111111111111111111111111111;
endcase
//Stage3
//--------------------------------------
//基準値遅延
ref_d1 <=tbl_ref;
//スロープパターンマスク
slope <=tbl_slope & msk;
//Stage4://1が立っている数のカウント
//--------------------------------------
//基準値遅延
ref_d2 <=ref_d1;
//1立っているの数
delta <=nc[4][5:0];//32以上は有りえないので下位6bitのみ保持
//Stage5:
//--------------------------------------
//基準値とΔ値を足す
add_delta <={1'b0,ref_d2} + {7'd0,delta};
//Stage6:クリッピング
//--------------------------------------
if(add_delta[12])
clip <=12'hFFF;
else
clip <=add_delta[11:0];
end
//=====================================================================
//ROM
//=====================================================================
table_rom ROM
(.clka (i_clk )
,.addra (buf_ff[15:5] )
,.douta (tbl )
);
endmodule
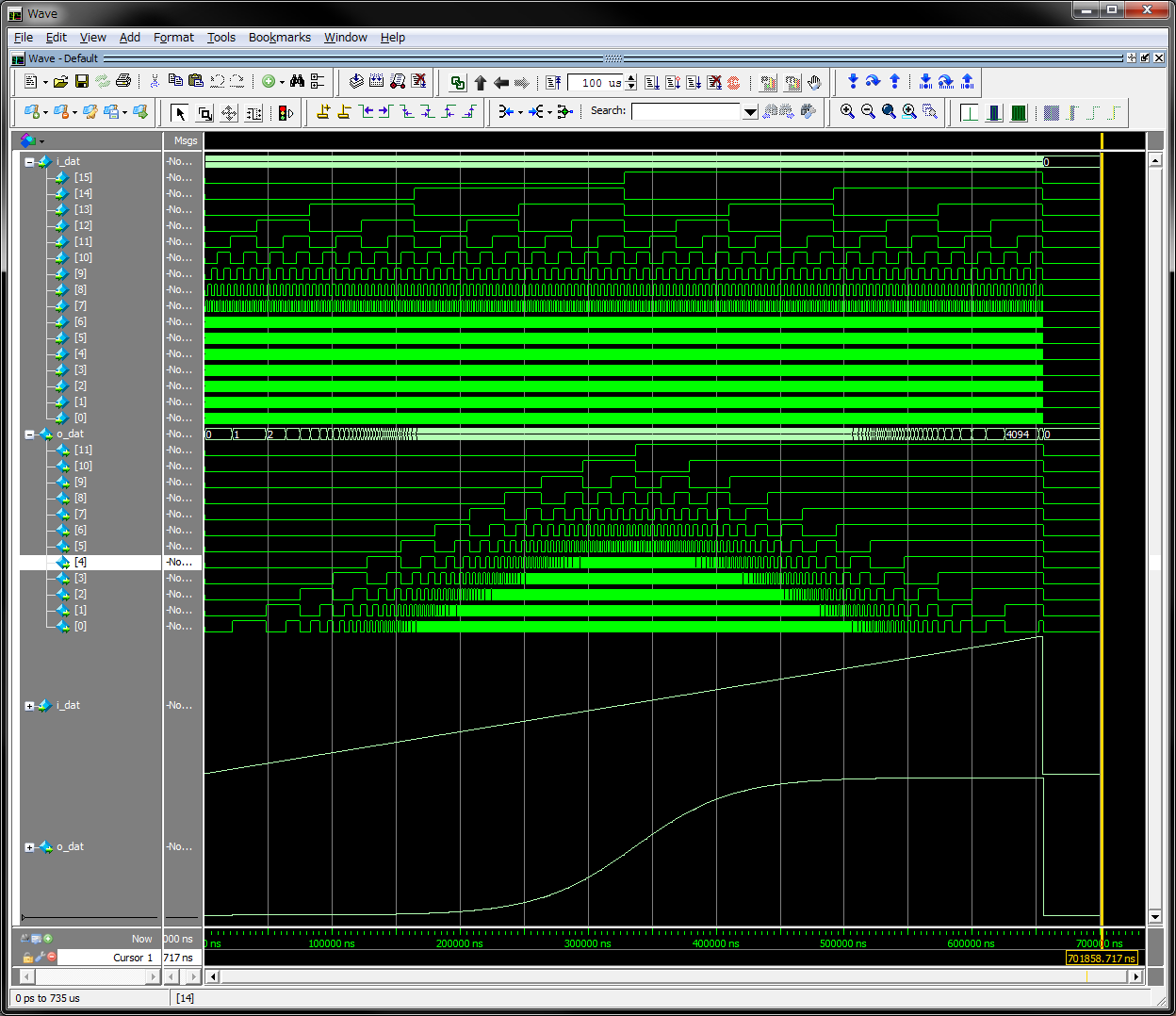
動作確認
In/Outの値を以下の順で表示した波形です。
- 入力X(16bit)バイナリ表示
- 出力Y(12bit)バイナリ表示
- 入力X(16bit)アナログ表示
- 出力Y(12bit)アナログ表示
入力インクリメントに対してシグモイド関数のS字カーブか出力されていることを確認できました。
(ModelSimのアナログ表示は便利ですね!)
応用例
今回はシグモイド関数ということでテーブルを作成しましたが、本回路では__”傾き1以下”__を満たしていればどのようなカーブでも対応可能な回路となっています。
例えばガンマ補正のカーブ等にも対応可能です。
今後の展開
今回作成した回路をCPUにぶら下がるアクセラレータとして使用したいので、前回作成した、CPUバスインターフェイスと連結してゆきたいと思います。