はじめに
本記事はHaskellアドベントカレンダー(その2)20日目の記事です。
最初にお断りしておきますが、Haskell要素はめちゃめちゃ薄いです。「ワンライナー」レベル。
お題は「Haskellで二次元配列のアクセスはどう書く?」といったところです。
Dammアルゴリズム
本記事を書くきっかけとなったDammアルゴリズムを紹介します。
Dammアルゴリズムは「チェックデジットの計算」に利用できるアルゴリズムです。チェックデジットとは、なにかを識別する数字の並び(シリアルナンバーやJISコードなど)が「正しい数字の並び」であるかを検査できるための数字です。
近年導入されたマイナンバーにも使用されているのですが、マイナンバーに導入されているチェックデジットは残念ながら容易に検査漏れが起こってしまうような作りになっているようです。
Dammアルゴリズムは、こういった数字の並びを検査するものとしては、「簡単な処理で検査符号が作れ、誤り検出性能も優秀」なものだそうです。詳しくはリンクの記事をご参照ください
第404号コラム「マイナンバーのチェックデジットについて」
ウィキペディア記事(英語)
Dammアルゴリズムによるチェックデジット生成
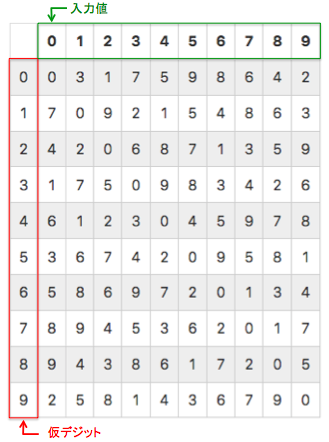
Dammアルゴリズムは10x10の固定テーブルを使用します。水平方向は入力の数値用、垂直方向は仮デジットの値用となります。仮デジットは入力値を処理する毎に更新されます。
今回は例として「573」という数値のチェックデジットを計算します。まず、仮デジットは初期値「0」としてスタートし、数値の上位の桁から処理します。数値の最初の桁は「5」なので、『仮デジット=0,入力値=5」に該当する数値を読み出します。この値は9なので、次の仮デジットが9となります。
次の桁は「7」です。仮デジットが9となったので、「仮デジット=9,入力値=7」に該当する数値を読み出します。今回は7なので、次の仮デジットが7となります。
3桁目の数値は3なので、今回も同様に「仮デジット=7,入力値=3」なので、仮デジットは5となります。桁はこれで終了なので、チェックデジットは「5」となります。
チェックデジットが正しいかどうかを検査するためには、「同じ手順でチェックデジットを計算して一致すれば合格」あるいは「入力の数値とチェックデジットを併せたもの(今回の例では5735)のチェックデジットを計算して、結果が「0」となれば検査合格」となります(仮デジットと入力値が同じ場合は仮デジットが全て0となっています)。
例でみたように、チェックデジット生成は「二次元配列を再帰的に読み出す」という処理なので、ループを使ってもかけますし、慣れている人なら「これは畳み込みだよね」となるかと思います。
例として、Pythonで書いてみます。ループさせるならこんな感じでしょう(何のひねりもありません)。
dammTable = [
[0, 3, 1, 7, 5, 9, 8, 6, 4, 2],
[7, 0, 9, 2, 1, 5, 4, 8, 6, 3],
[4, 2, 0, 6, 8, 7, 1, 3, 5, 9],
[1, 7, 5, 0, 9, 8, 3, 4, 2, 6],
[6, 1, 2, 3, 0, 4, 5, 9, 7, 8],
[3, 6, 7, 4, 2, 0, 9, 5, 8, 1],
[5, 8, 6, 9, 7, 2, 0, 1, 3, 4],
[8, 9, 4, 5, 3, 6, 2, 0, 1, 7],
[9, 4, 3, 8, 6, 1, 7, 2, 0, 5],
[2, 5, 8, 1, 4, 3, 6, 7, 9, 0]
]
# inputは文字列とする
digit = 0
for char in list(input):
digit = dammTable[digit][int(char)]
Pythonでは、畳み込みはreduceなので、無名関数を使った実装なこんな感じになります。仮デジットのみが畳み込みで保持すべき情報ですので、畳み込みの実装も非常にシンプルです。実質「二次元配列を読み出すだけ」です。
digit = reduce(lambda digit, char: dammTable[digit][int(char)], list(input), 0)
Haskellで実装してみる
ここまでながーい前振りでしたが、DammアルゴリズムによるチェックデジットをHaskellで書いてみます。Haskellではループではなく畳み込みで実装するのが定石でしょう。Pythonのreduceを使ったスタイルとほぼ同じスタイルになります。
dammTable :: [[Int]]
dammTable =
[ [0, 3, 1, 7, 5, 9, 8, 6, 4, 2]
, [7, 0, 9, 2, 1, 5, 4, 8, 6, 3]
, [4, 2, 0, 6, 8, 7, 1, 3, 5, 9]
, [1, 7, 5, 0, 9, 8, 3, 4, 2, 6]
, [6, 1, 2, 3, 0, 4, 5, 9, 7, 8]
, [3, 6, 7, 4, 2, 0, 9, 5, 8, 1]
, [5, 8, 6, 9, 7, 2, 0, 1, 3, 4]
, [8, 9, 4, 5, 3, 6, 2, 0, 1, 7]
, [9, 4, 3, 8, 6, 1, 7, 2, 0, 5]
, [2, 5, 8, 1, 4, 3, 6, 7, 9, 0]
]
-- inputの型は[Int]とする
digit = foldl (\digit char -> (dammTable !! digit) !! char) 0 input
これで何の問題もないのですが、この実装をした時に「foldlの引数である無名関数は、もっとすっきり書けるんじゃないの?」という声が聞こえてくるわけです。なんとなく「ポイントフリーに書けるだろう」とは思うものの、2引数関数のポイントフリー化は慣れが必要なことがありますよね。
これをやってみた当時は、なんとなく試行錯誤をして「コンパイルが通った始めての形」が正解でしたが、ここではちゃんと導出してみます。基本的な流れは「中間演算子を関数の形にする→引数を追い出す」というものです。
dammFunc :: Int -> Int -> Int
-- x y を引数に取る(ポイントフリーではない)スタイル
dammFunc x y = (dammTable !! x) !! y
-- yを引数にとる中間演算子「!!」を関数スタイルにする
dammFunc x y = (!!) (dammTable !! x) y
-- 両辺にyが末尾にあるので、yが削除できる
dammFunc x = (!!) (dammTable !! x)
-- xを引数にとる中間演算子「!!」を関数スタイルにする
dammFunc x = (!!) ((!!) dammTable x))
-- 「(!!) dammTable」を括弧でくくり、1つの関数とみなす
dammFunc x = (!!) (((!!) dammTable) x))
-- f (g x) = (f . g) x による変形(f = (!!), g = (!!) dammTable)
dammFunc x = ((!!) . (!!) dammTable)) x
-- 両辺にxが末尾に来たので、xが削除できる
dammFunc = (!!) . (!!) dammTable
ポイントフリースタイルだと、こんなすっきりした形になりました。これを使って書き換えると、下記のようになります。二次元配列アクセスをする関数がfoldlの引数としてすっきりおさまっている様は格好いいなぁ、と思います。
digit = foldl ((!!) . (!!) dammTable) 0 input
感想(まとめにかえて)
関数型ではない言語は、「=」は「代入」であり、左から右への流れ、というイメージが強いですが、Haskellでは「両辺が等しい」というイメージがあり、なんとなく「同値変形」している感がありますね(あくまでイメージですが)。