パラメトリック曲面を描くのに適した WebGL ライブラリについて

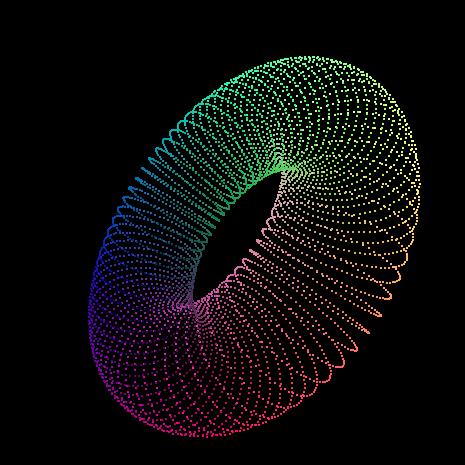
この記事は WebGL Advent Calendar 2015 の６日目の記事です。

パラメトリック曲面について

みなさん、パラメトリック曲面という言葉をご存じでしょうか？
２つのパラメータ（時間や角度などの媒介変数）によって決まる曲面のことを、パラメトリック曲面と呼ぶようです。

こんなのです。

Parametrische Flächen und Körper

こんな図形が手軽に描けたらワクワクしてきませんか？

今回は「lightgl.js」という軽量 WebGL ライブラリを使いたいと思います。
まずは、三角形からです。

一番シンプルな例

index.html

<script src="lightgl.js"></script>

index.js

var gl = GL.create();

gl.ondraw = function() {
    gl.clearColor(1.0, 1.0, 1.0, 1.0);
    gl.clear(gl.COLOR_BUFFER_BIT);
    gl.translate(0, 0, -2.5);
    gl.color(0.0, 0.0, 1.0);
    gl.begin(gl.LINE_STRIP);
    gl.vertex( 0.0, 0.5, 0.0);   // 頂点１
    gl.vertex(-0.5,-0.5, 0.0);   // 頂点２
    gl.vertex( 0.5,-0.5, 0.0);   // 頂点３
    gl.end();
};

いかがでしょうか？エラーにならなければ三角形が描画されたかと思います。
基本的にパラメトリック曲面は gl.vertex() を用いて、3D 空間にプロットすることで実現します。

次にトーラスを描いてみましょう。

トーラスの例

式は以下になります。

x = (R + r * cos(v)) * cos(u)
y = (R + r * cos(v)) * sin(u)
z = r * sin(v)

u は 0 ～ 2π
v は 0 ～ 2π

index.js

var angle = 0;
var gl = GL.create();

gl.onupdate = function(seconds) {
    angle += 45 * seconds;
};

gl.ondraw = function() {
    gl.clearColor(0.0, 0.0, 0.0, 1.0);
    gl.clear(gl.COLOR_BUFFER_BIT | gl.DEPTH_BUFFER_BIT);
    gl.loadIdentity();
    gl.translate(0, 0, -2);
    gl.rotate(60, 1, 0, 0);
    gl.rotate(angle, 1, 1, 1);

    // トーラス（Torus）の座標データを用意
    //             1.0 y 
    //              ^  -1.0 
    //              | / z
    //              |/       x
    // -1.0 -----------------> +1.0
    //            / |
    //      +1.0 /  |
    //           -1.0
    // 
    gl.begin(gl.POINTS);
    gl.pointSize(2.0);
    var ustep = Math.PI * 5 / 180;
    var vstep = Math.PI * 5 / 180;
    var R = 0.5;
    var r = 0.2;
    for (var v = 0; v <= 2 * Math.PI; v += vstep) {
        for (var u = 0; u <= 2 * Math.PI; u += ustep) {
            var x = (R + r * Math.cos(v)) * Math.cos(u);
            var y = (R + r * Math.cos(v)) * Math.sin(u);
            var z = r * Math.sin(v);
            gl.color(x + 0.5, y + 0.5, z + 0.5, 1.0);
            gl.vertex(x, y, z);
        }
    }
    gl.end();
};

gl.fullscreen();
gl.animate();

lightgl.js の特徴

今回、lightgl.js を選んだのは以下の理由によります。

• ライブラリが軽量（100KB以下）
• 少ないコードで WebGL が使えるようになる。
• 書き方が OpenGL に似ている（OpenGL を知っていれば移植が簡単）
• 軽量ラッパである為、無駄が少ない（組み込み関数、組み込みシェーダ等は最低限のもしか用意されていない為、軽い）

ライブラリを使わないスクラッチの WebGL だと、先述のような簡単な三角形でも100行は軽く超えるので、ライブラリの恩恵が感じられるのではないでしょうか。

OpenGL / lightgl.js / processin.js との比較

OpenGL	lightgl.js	processing.js
float	var	var
int	var	var
sin()	Math.sin()	Math.sin()
cos()	Math.cos()	Math.cos()
glBegin()	gl.begin()	p.beginShape()
glEnd()	gl.end()	p.endShape()
glColor3d()	gl.color()	p.stroke()※
glPointSize()	gl.pointSize()	p.strokeWeight()
glVertex3d()	gl.vertex()	p.vertex()
GL_POINTS	gl.POINTS	p.POINTS
GL_LINES	gl.LINES	p.LINES
GL_LINE_STRIP	gl.LINE_STRIP	p.LINE_STRIP

※ processing.js の stroke 関数の色指定は 0～1 でなく 0～255 である為、注意。

パラメトリック曲面およびその他サンプル

ということで、色々と描画してみました。パラメトリック曲面でないものもありますが、ご了承ください。

タイトル	イメージ	lightgl.js	processing.js	Three.js	WebGL
三角形		Link	Link	Link	Link
リサージュ図形		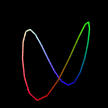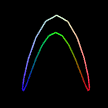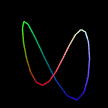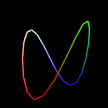Link	Link	Link	Link
３次元リサージュ図形		Link	Link	Link	Link
ハーモノグラフ		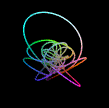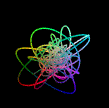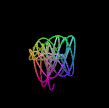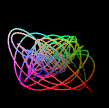Link	Link	Link	Link
３次元関数		Link	Link	Link	Link
波動方程式		Link	Link	Link	-
ローマ曲面		Link	Link	Link	-
貝殻曲面		Link	Link	Link	-
リンゴ曲面		Link	Link	Link	-
スライム曲面		Link	Link	Link	-
ハート曲面		Link	Link	Link	-
トーラス		Link	Link	Link	-
Wave Ball		Link	Link	Link	-

追記（パフォーマンスについて）

コメント欄にて @emadurandal さんに教えて頂いたのですが、gl.vertex() は３次元空間にプロットするという意味合いでは分かりやすいのですが、パフォーマンスの観点からすると、かなり非効率なやり方のようです。
WebGL 的なテクニックとしては、VBO（頂点バッファオブジェクト）を使うことが推奨されているようです。

詳しくは、@emadurandal さんの９日目の記事「GPU本来の性能を引き出すWebGL頂点データ作成法 」を参照下さい。

また、lightgl.js でも VBO による描画モードが用意されています。サンプルについては、下記の「VBO 編」をご覧ください。

各種 WebGL ライブラリで基本図形を表示してみる
http://qiita.com/cx20/items/0fa19c96aa6470d98807