ビンパッキング問題を利用してクラウド利用料を安くする

ビンパッキング問題を利用したクラウド利用の最適化

さて、AWSやAzure、GCPのようなクラウドを利用していると、どのアプリケーションをどのサイズの仮想マシンに登載すれば効率的なのか、迷うことがあります。
アプリケーションのCPU、メモリ、ディスク利用量が判明しているとして、アプリケーションをどのサイズの仮想マシンに入れれば良いか、コロケーションした方が良いのか、分散した方が良いのか・・・いろいろと考えることはあります。
クラウド利用歴の長い技術者は経験則でどのサイズを選ぶのか、わかったりするもののようです。
しかし今回はちょっとアプローチを変えて、最適化問題として解決策を見出だせないかな、と考えてみました。

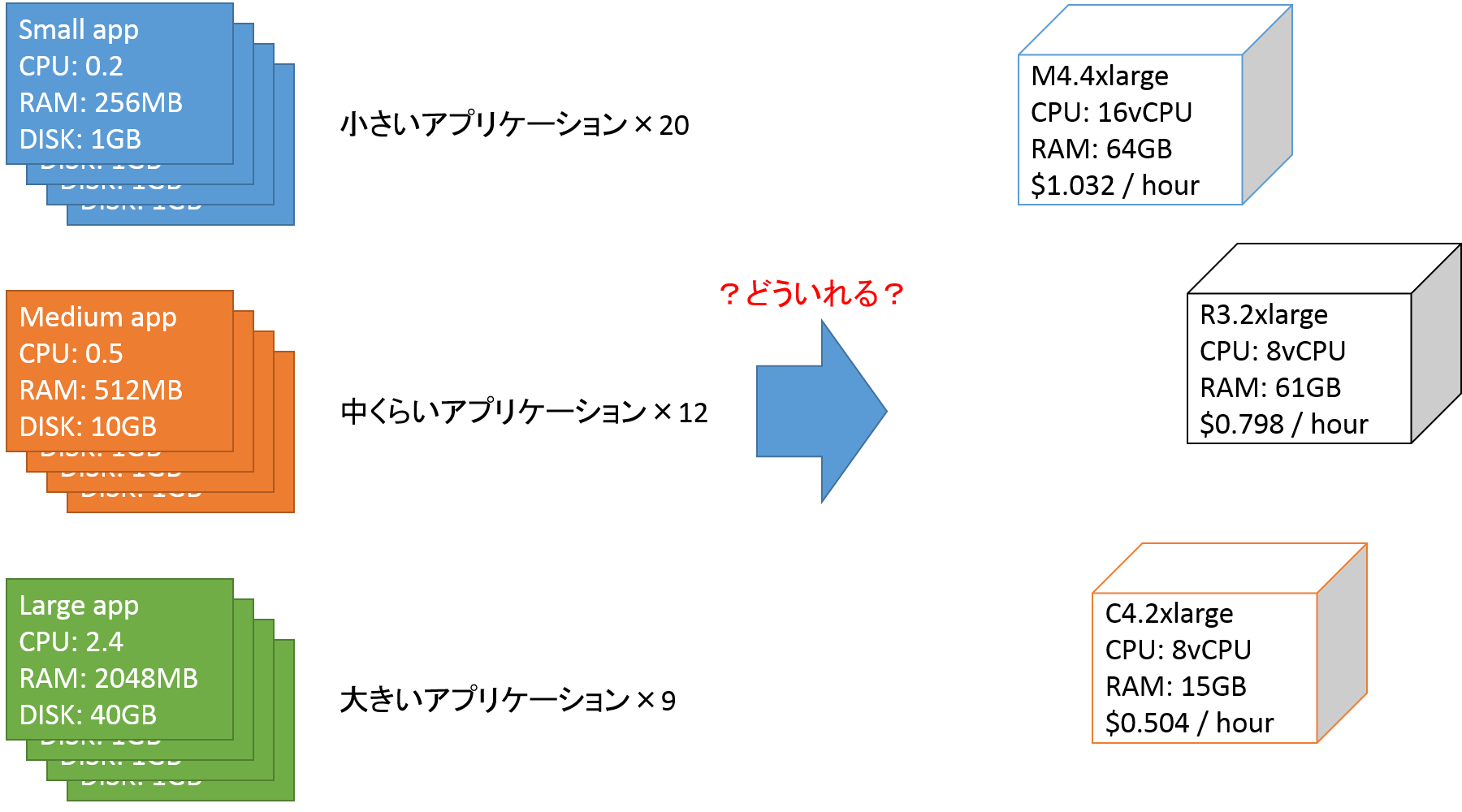
例えば以下のような状況で、どのサイズのアプリケーションをどのサイズの仮想マシンに入れれば、効率的でしょうか？

まずはおことわり

最適化問題が面白そうだったので、勉強がてら、自分にとって身近な問題で考えてみました。
最適化問題歴１週間なので、間違っている箇所やアドバイスはご指摘ください。

なお、勉強に使ったのは以下の本です。
Python言語によるビジネスアナリティクス 実務家のための最適化・統計解析・機械学習

問題設定

今回は必要な数のアプリケーションをクラウドの仮想マシンに登載した結果、費用が一番安くなる構成を、ビンパッキング問題として求めたいと思います。

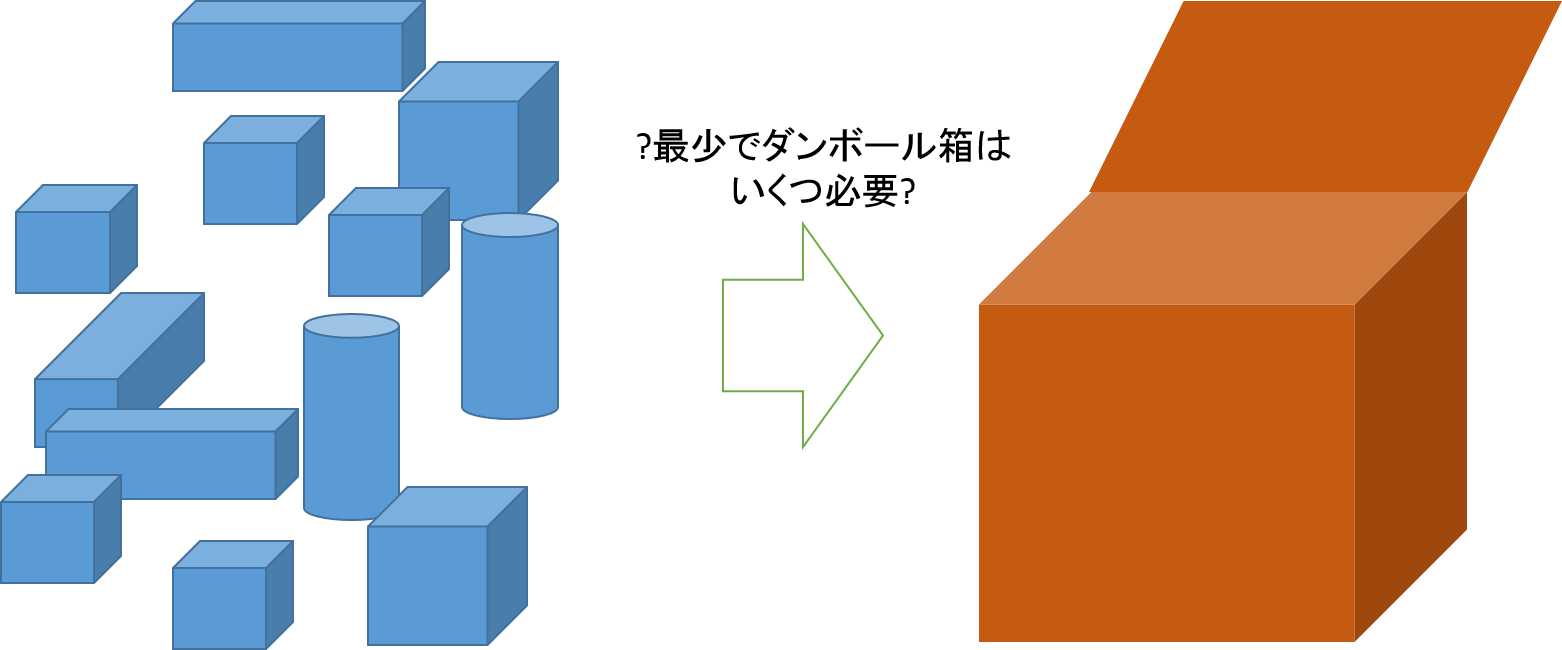
ビンパッキング問題とは、ある入れ物（箱やビン、コンテナ）に荷物（重さや個数が定められている）を詰める際、必要な入れ物の最少数を求める組み合わせ最適化問題です。
例えば、引っ越しの際に荷物をダンボールに詰めると思いますが、そのダンボールの数を最少にする詰め方を解くものです。

荷物をダンボールに詰めるのであれば、ダンボール箱の体積（横×縦×高）と耐荷重量に対し、荷物の体積と重さを考慮して入れます。
これを見た時、荷物をアプリケーション、ダンボールを仮想マシンとして、体積や重さをCPU, RAM, Disk, 費用に置き換えれば、クラウドの仮想マシン利用を最適化することができる気がしたのが、今回の発端です。

環境

Pythonで最適化問題を解いてみたいと思います。
Pythonでは最適化問題を解くのに便利なライブラリが色々提供されていまして、ここに詳しく説明されています。
最適化におけるPython

今回はPython3.5(Anaconda)でopenoptを使いました。
OSはCentOS7.3です。
Openoptは数理最適化のモデルを作るライブラリです。

この環境へのopenoptのインストール方法は以下のとおりです。

conda install --channel https://conda.anaconda.org/cachemeorg funcdesigner openopt
pip install cvxopt
pip install glpk

やること

今回はアプリケーションを３種類に分けます。
小さいアプリケーション、中くらいのアプリケーション、大きいアプリケーションです。
それぞれのリソース利用量は以下とします。

小さいアプリケーション	中くらいのアプリケーション	大きいアプリケーション
CPU: 0.2	CPU: 0.5	CPU: 2.4
RAM: 256MB	RAM: 512MB	RAM: 2048MB
DISK: 1GB	DISK: 10GB	DISK: 40GB

これらを以下のEC2インスタンスサイズのうち、どれに詰め込むと一番安くなるか、ビンパッキング問題を使って解きます。

M4.4xlarge	R3.2xlarge	C4.2xlarge
CPU: 16vCPU	CPU: 8vCPU	CPU: 8vCPU
RAM: 64GB	RAM: 61GB	RAM: 15GB
Disk: 100GB	Disk: 100GB	Disk: 100GB
$1.032 / hour	$0.798 / hour	$0.504 / hour

なお、単価は本日（2017年5月21日）時点の東京リージョンでLinuxのオンデマンドインスタンスを使った場合の値段としています。参考
また、ディスクの費用（EBS）は含んでおりません。

プログラム

プログラム全文はこちらです。

# import openopt
from openopt import *

# 小さいアプリケーション、中くらいのアプリケーション、大きいアプリケーションの数を設定します。
small_num = 20
med_num = 12
large_num = 9

apps = []

# 各アプリケーションのリソース利用量をdictにし、リストに追加します。
for i in range(small_num):
    small_app = {
        'name': 'small%d' % i,
        'cpu': 0.2,
        'mem': 256,
        'disk': 1
        }
    apps.append(small_app)

for i in range(med_num):
    med_app = {
        'name': 'medium%d' % i,
        'cpu': 0.5,
        'mem': 512,
        'disk': 10
        }
    apps.append(med_app)
    
for i in range(large_num):
    large_app = {
        'name': 'large%d' % i,
        'cpu': 2.4,
        'mem': 2048,
        'disk': 40
        }
    apps.append(large_app)


# AWS EC2インスタンスのサイズを設定します。
# 各リソースを9掛けにしているのは、OSがリソースの10%を使うと仮定しているためです。
instance_sizes = [
    {
        'name': 'm4.x4large',
        'cost': 1.032 * 24 * 30,
        'size': {
            'cpu': 16 * 0.9,
            'mem': 64 * 1024 * 0.9, 
            'disk': 1000 * 0.9
        }
    },
    {
        'name': 'r3.2xlarge',
        'cost': 0.798 * 24 * 30,
        'size': {
            'cpu': 8 * 0.9,
            'mem': 61 * 1024 * 0.9, 
            'disk': 1000 * 0.9
        }
    },
    {
        'name': 'c4.2xlarge',
        'cost': 0.504 * 24 * 30,
        'size': {
            'cpu': 8 * 0.9,
            'mem': 15 * 1024 * 0.9, 
            'disk': 1000 * 0.9
        }
    }
]

# ビンパッキングです。
# openoptのBPPという関数を使います。
def bin_pack_instance(apps, instance_size):
    cost = instance_size['cost']    
    p = BPP(apps, instance_size['size'], goal = 'min')
    r = p.solve('glpk', iprint = 0)
    instances = len(r.xf)
    total_cost = instances * cost
    return r, instances, total_cost

# 実行します。
# 各インスタンスサイズでビンパッキングを行い、最も安くなるものを探します。
if __name__ == '__main__':
    list_cost = []
    for instance in instance_sizes:
        r, instances, total_cost = bin_pack_instance(apps, instance)
        list_cost.append({'instance': instance['name'], 'total_cost': total_cost})

        print("\r") 
        print("Bin packing for : {0}".format(instance['name']))
        print("Total number of apps is " + str(len(apps)))
        print("Total {0} instance used is {1}".format(instance['name'], instances))
        print("Total cost is {0}".format(total_cost))

        for i,s in enumerate(r.xf):
            print ("Instance {0} contains {1} apps".format(i, len(s)))
            print("\t CPU: {0}vCPU\t RAM: {1}MB\t Disk: {2}GB"
                  .format(r.values['cpu'][i], r.values['mem'][i], r.values['disk'][i]))
            print("\t Contains: {0}".format(r.xf[i]))

        print("\r")  
    
    print("Result: {0}".format(list_cost))

結果はこちらのとおりになります。

------------------------- OpenOpt 0.5625 -------------------------
problem: unnamed   type: MILP    goal: min
solver: glpk
  iter  objFunVal  log10(maxResidual)  
    0  0.000e+00               0.00 
    1  0.000e+00            -100.00 
istop: 1000 (optimal)
Solver:   Time Elapsed = 0.12 	CPU Time Elapsed = 0.12
objFuncValue: 3 (feasible, MaxResidual = 0)

Bin packing for : m4.x4large
Total number of apps is 41
Total m4.x4large instance used is 3
Total cost is 2229.12
Instance 0 contains 18 apps
	 CPU: 14.200000000000001vCPU	 RAM: 13312.0MB	 Disk: 228.0GB
	 Contains: ('small0', 'small3', 'small4', 'small5', 'small6', 'small7', 'small8', 'small13', 'medium0', 'medium1', 'medium2', 'medium3', 'medium4', 'medium5', 'large3', 'large4', 'large6', 'large7')
Instance 1 contains 17 apps
	 CPU: 14.4vCPU	 RAM: 13312.0MB	 Disk: 212.0GB
	 Contains: ('small1', 'small2', 'small9', 'small10', 'small11', 'small12', 'small14', 'small15', 'small16', 'small17', 'small18', 'small19', 'large0', 'large1', 'large2', 'large5', 'large8')
Instance 2 contains 6 apps
	 CPU: 3.0vCPU	 RAM: 3072.0MB	 Disk: 60.0GB
	 Contains: ('medium6', 'medium7', 'medium8', 'medium9', 'medium10', 'medium11')


------------------------- OpenOpt 0.5625 -------------------------
problem: unnamed   type: MILP    goal: min
solver: glpk
  iter  objFunVal  log10(maxResidual)  
    0  0.000e+00               0.00 
    1  0.000e+00            -100.00 
istop: 1000 (optimal)
Solver:   Time Elapsed = 0.24 	CPU Time Elapsed = 0.23
objFuncValue: 5 (feasible, MaxResidual = 0)

Bin packing for : r3.2xlarge
Total number of apps is 41
Total r3.2xlarge instance used is 5
Total cost is 2872.8
Instance 0 contains 3 apps
	 CPU: 7.199999999999999vCPU	 RAM: 6144.0MB	 Disk: 120.0GB
	 Contains: ('large0', 'large4', 'large7')
Instance 1 contains 11 apps
	 CPU: 7.199999999999999vCPU	 RAM: 6912.0MB	 Disk: 107.0GB
	 Contains: ('small5', 'small6', 'small7', 'small8', 'small9', 'small18', 'small19', 'medium0', 'medium1', 'large1', 'large2')
Instance 2 contains 13 apps
	 CPU: 7.0vCPU	 RAM: 6912.0MB	 Disk: 91.0GB
	 Contains: ('small0', 'small1', 'small2', 'small10', 'small11', 'small12', 'small13', 'small14', 'small15', 'small16', 'small17', 'large5', 'large6')
Instance 3 contains 8 apps
	 CPU: 7.199999999999999vCPU	 RAM: 6656.0MB	 Disk: 122.0GB
	 Contains: ('small3', 'small4', 'medium2', 'medium3', 'medium4', 'medium5', 'large3', 'large8')
Instance 4 contains 6 apps
	 CPU: 3.0vCPU	 RAM: 3072.0MB	 Disk: 60.0GB
	 Contains: ('medium6', 'medium7', 'medium8', 'medium9', 'medium10', 'medium11')


------------------------- OpenOpt 0.5625 -------------------------
problem: unnamed   type: MILP    goal: min
solver: glpk
  iter  objFunVal  log10(maxResidual)  
    0  0.000e+00               0.00 
    1  0.000e+00            -100.00 
istop: 1000 (optimal)
Solver:   Time Elapsed = 0.14 	CPU Time Elapsed = 0.14
objFuncValue: 5 (feasible, MaxResidual = 0)

Bin packing for : c4.2xlarge
Total number of apps is 41
Total c4.2xlarge instance used is 5
Total cost is 1814.4
Instance 0 contains 7 apps
	 CPU: 5.4vCPU	 RAM: 5120.0MB	 Disk: 100.0GB
	 Contains: ('medium0', 'medium1', 'medium2', 'medium3', 'medium4', 'medium5', 'large6')
Instance 1 contains 15 apps
	 CPU: 7.0vCPU	 RAM: 7168.0MB	 Disk: 108.0GB
	 Contains: ('small8', 'small9', 'small10', 'small14', 'small16', 'small17', 'small18', 'small19', 'medium6', 'medium7', 'medium8', 'medium9', 'medium10', 'medium11', 'large0')
Instance 2 contains 14 apps
	 CPU: 7.199999999999999vCPU	 RAM: 7168.0MB	 Disk: 92.0GB
	 Contains: ('small0', 'small1', 'small2', 'small3', 'small4', 'small5', 'small6', 'small7', 'small11', 'small12', 'small13', 'small15', 'large3', 'large4')
Instance 3 contains 3 apps
	 CPU: 7.199999999999999vCPU	 RAM: 6144.0MB	 Disk: 120.0GB
	 Contains: ('large1', 'large2', 'large5')
Instance 4 contains 2 apps
	 CPU: 4.8vCPU	 RAM: 4096.0MB	 Disk: 80.0GB
	 Contains: ('large7', 'large8')

Result: [{'instance': 'm4.x4large', 'total_cost': 2229.12}, {'instance': 'r3.2xlarge', 'total_cost': 2872.8}, {'instance': 'c4.2xlarge', 'total_cost': 1814.4}]

長くなりますが、結果としてc4.2xlargeを4台に詰め込むのが最も効率が良く、月額$1814.4で済むようです。

感想

今回はアプリケーション配置を最適化問題として考えてみました。
もちろん同一サイズのインスタンスに全アプリケーションを詰め込むケースは少ないでしょうし、サブネット分離等々、アーキテクチャを考える上で考えなければならない点は多いです。
本当は複数インスタンスサイズを混ぜた構成（c4.2xlarge 3台、t2.micro 4台、みたいな）を算出したかったのですが、サイズの違う複数ビンでのパッキング方法がわからず、このような形になりました。
これは今後の課題にします。
もし詳しい方がおりましたら、教えて下さい。

参考

組合せ最適化を使おう
組合せ最適化 - 標準問題と実行方法
最適化におけるPython
ビンパッキング問題の解き方
Python言語によるビジネスアナリティクス 実務家のための最適化・統計解析・機械学習
https://github.com/PythonCharmers/OOSuite/blob/master/OpenOpt/openopt/examples/bpp_2.py