物体検出の評価指標であるmAPの算出方法を詳しく説明している記事が少なかったのでまとめました.
修論執筆に際してかなり丁寧にまとめたつもりです.

mAP(Mean Average Precision), AP(Average Precision)は物体検出の精度を比較するための指標です.
これらを理解するためには,TP(True Positive), FP(False Positive), FN(False Negative), TN(True Negative), Precision, Recallの概念と,物体検出において重要なIoU(Intersection over Union)の概念を知る必要があります.
画像分類と物体検出ではTP,FP,FN,TNの指す意味が異なってきます.
そこで,この記事ではそれらの違いを明確にするために
- 1. TP, FP, FN, TN, Precision, Recall (ガンの場合)
- 2. TP, FP, FN, TN, Precision, Recall (画像分類の場合)
- 3. IoU
- 4. TP, FP, FN, TN, Precision, Recall (物体検出の場合)
- 5. AP. mAP
という流れで説明していきたいと思います.
1. TP, FP, FN, TN, Precision, Recall (ガンの場合)
まず、物体検出における説明の前に, これらの評価指標がどのような経緯で使われてきたのかというお話からさせてください.
TP, FP, FN, TN, Precision, Recallなどの評価指標は従来,ガンの検査結果が実際にガンであるかといった事象を評価するために用いられてきました.
いわゆる陽性,陰性といった概念です.
検査(予測)結果である陽性はPositive,陰性はNegativeを指します.
そして,陽性や陰性の検査結果が実際に正しければTrue,陽性や陰性の検査結果が実際に正しくなければFalseとして表します.
ですので,ガンの場合,
- TP(True Positive): 検査結果はガンであり,実際にもガンだった.
- FP(False Positive): 検査結果はガンであったが,実際にはガンではなかった.
- FN(False Negative): 検査結果はガンではなかったが,実際にはガンだった.
- TN(True Negative): 検査結果はガンではなく,実際にもガンではなかった.
| 実際はガン | 実際はガンでない | |
|---|---|---|
| 検査結果はガン(陽性) | TP | FP |
| 検査結果はガンでない(陰性) | FN | TN |
ということになります.
そしてPrecisionとRecallはこれらを用いて以下のように表せます.
Precision = \frac{TP}{TP + FP}
Recall = \frac{TP}{TP + FN}
すなわち,
Precision = \frac{陽性と出た検査結果が実際にガンであった数}{陽性と出た検査結果の総数}
Recall = \frac{実際にガンであった事例のうち陽性と検査結果が出ていた数}{実際にガンであった事例の総数}
となります.
もう少し詳しく見てみましょう.
Precisionは,「陽性と出た検査結果の総数の内,実際にガンであった(正しくガンと検査できた)割合」を表します.
Precisionは一般には,「検査(予測)の精度」を見るための指標であり、Precisionの値が大きいほど検査(予測)の精度が確からしいということを表します.
しかしながら,Precisionの評価指標だけでは,「実際にはガンであったのに検査結果がガンでないとして取りこぼした場合」の精度を測ることができません.これを取りこぼしてしまうと命に関わる致命的なミスになりかねません.
この「取りこぼしのなさ」を測る評価指標がRecallというわけです.
Recallは,「実際はガンであった全ての事例の内,陽性と(正しく)検査できた割合」を表します.(分子の値としてはPrecisionとRecallの式で同じTPなのですが, 検査結果を基準に見るのか, 実際にガンであるかのどちらの基準で見るかという点ではニュアンスが異なることが分かると思います.)
Recallは一般には,「検査による取りこぼしの少なさ」を見るための指標であり、大きな値であるほどこの取りこぼしの少なさを表すことになります.
蛇足ですが,自動車などに欠陥・不備があり企業が回収することをリコールと言いますよね.評価指標のRecallが表すのは検査(予測)結果の真値に対する再現率≒回収率ということなので、根本は同じ概念のように思います.覚え方として使う分には良いのではないでしょうか.
2. TP, FP, FN, TN, Precision, Recall (画像分類の場合)
画像分類の場合,ガンのときと同じようにTPなどの概念を適用することができます.
ここでは「StopSign, TrafficLight, Car」の3クラスの分類を例に取ってみましょう.
StopSignのクラスを対象に評価する場合、
- TP(True Positive): 予測結果のラベルはStopSignであり,正解データのラベルもStopSignだった.
- FP(False Positive): 予測結果のラベルはStopSignであったが,正解データのラベルはStopSignではなかった.(TrafficLightかCarだった)
- FN(False Negative): 予測結果のラベルはStopSignではなかったが,正解データのラベルはStopSignだった.
- TN(True Negative): 予測結果のラベルはStopSignではなく,正解データのラベルもStopSignではなかった.(TrafficLightかCarだった)
| 正解データのラベルがStopSign | 正解データのラベルがStopSignでない | |
|---|---|---|
| 予測結果がStopSign | TP | FP |
| 予測結果がStopSignでない | FN | TN |
そしてPrecisionとRecallはこれらを用いて以下のように表せます.
Precision = \frac{TP}{TP + FP}
Recall = \frac{TP}{TP + FN}
すなわち,
Precision = \frac{StopSignと予測した数のうち本当にStopSignであった数}{StopSignと予測した総数}
Recall = \frac{正解データのStopSignラベルの数のうちStopSignと予測できた数}{正解データのStopSignラベルの総数}
となります.
他のクラス「TrafficLight, Car」についても同様に計算できますね.
3. IoU
「それでは,早速これを物体検出の例に当てはめてみましょう」と言いたいところなのですが,
その前に**IoU(Intersection over Union)**と呼ばれる概念を説明する必要があります.
物体検出と画像分類の根本的な違いはなんだと思いますか?
それは「クラスの分類すること」に加えて「物体の領域を検出すること」です.
物体検出の評価指標では、画像分類のときとは異なり「物体の領域を検出すること」を含めて評価する必要があり、物体の領域を予測した際の精度を算出する際に使われる概念がIoUなのです.
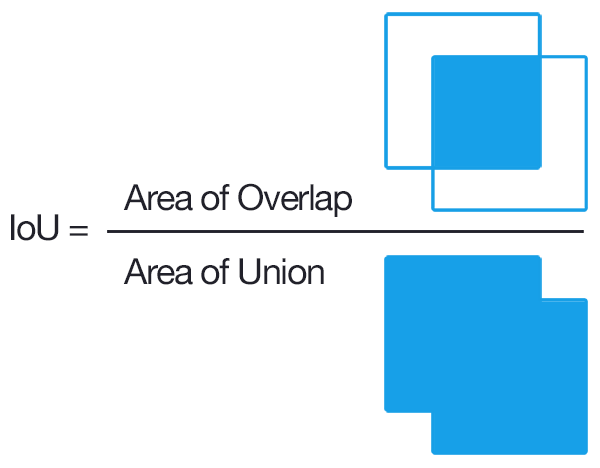
IoUとはIntersection over Unionという名前の通り,2つの領域を見て,その**「領域の積:Intersection」を「領域の和:Union」で「割る:over」**することです.
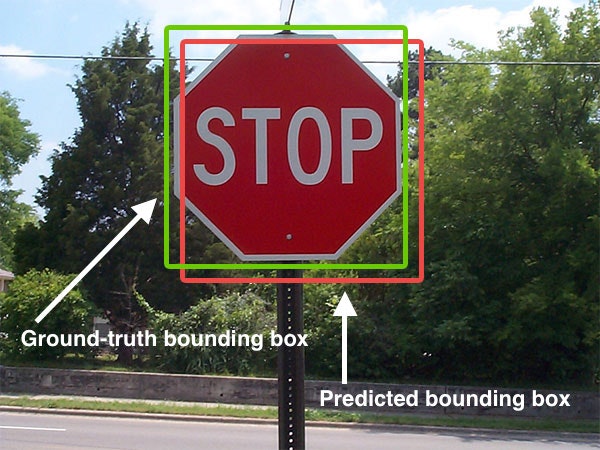
物体検出ではBouding Boxと呼ばれる矩形状の境界線で物体を検出しますが,IoUを使うことで,
このBounding Boxが**「予測されたもの:Predicted Bouding Box」と「真値:Ground-truth Bounding Box」**の2つのBounding Boxの「2つの領域がどれだけ重なっているのか[0,1]の値で見る」ことができます.
この数値が何を表しているかと言うと,
- IoU = 0 ⇨ 2つのBounding Boxが全く重なっていない
- IoU = 1 ⇨ 2つのBounding Boxが完全に重なっている
ということです.
もちろん完全に重なるケースは稀で,[0,1]の中間値を中間値を取る事が多いのですが、IoUの値の変化によって重なりも以下の図のように変化します.
4. TP, FP, FN, TN, Precision, Recall (物体検出の場合)
ではこのIoUを用いて物体検出のTP, FP, FN, TN, Precision, Recallを算出していきます.
例として,
Label = ["StopSign", "TrafficLight", "Car"]
の3つのクラスで物体検出するモデルを扱いましょう.
その3つのクラスの内,「StopSign」について考えることにします.
3クラスのデータで学習させた物体検出モデルを用いて以下の表に示す結果が得られたとします.
表1."StopSign"と予測されたPredicted BBoxの検出結果(TP,FP)
| Sorted Number | Confidence Score(%) | Correct? |
|---|---|---|
| #1 | 96 | True |
| #2 | 92 | True |
| #3 | 89 | False |
| #4 | 88 | False |
| #5 | 84 | False |
| #6 | 83 | True |
| #7 | 80 | True |
| #8 | 78 | False |
| #9 | 74 | False |
| #10 | 72 | True |
こちらの表は,物体検出モデルが「StopSign」と検出した結果で,
信頼度スコア:Confidence Score順にソートしたものです.
(※信頼度スコアを簡潔に言うと,クラスの物体をそのBounding Boxがどれくらいの確率で含んでいるのかを表すスコアです.詳しくはこちらの記事を参照してください.)
ここでCorrect?の列は,
10個全てのPredicted Bounding Boxの内,IoU ≥ 0.5 であるものはTrue,それ以外はFalseと示しています.
このTrueと示しているものがTPに当たり,Falseと示しているものがFPに当たります.
TP, FPだけでなく,
ここで,予測BBox(Predicted Bounding Box)が正解BBox(Ground-truth Bounding Box)として、
物体検出の場合のTP, FP, FN, TN全てをまとめると,
- TP: StopSignの予測BBoxがどれかの正解BBoxと紐づいていてIoU ≥ 0.5で十分に重なっている(検出された上で正しい)
- FP: StopSignの予測BBoxがどれかの正解BBoxと紐づいていてIoU < 0.5で十分に重なっていない(検出されたが間違い)
- FN: StopSignの正解BBoxがどの予測BBoxとも紐づいていない(検出されなかったが間違い)
- TN: 正解BBoxでない箇所を検出しなかった(検出されなかったことが正しい)ケースは取りうる箇所としては無数に考えられるため、True Negative (TN) は定義しない
| 正しい | 間違い | |
|---|---|---|
| 検出された | TP | FP |
| 検出されなかった | TN(定義しない) | FN |
少々画像分類と比較して特殊ですが上記のようになります.
そしてPrecisionとRecallは以下で表せます.
Precision = \frac{TP}{TP + FP}
Recall = \frac{TP}{TP + FN}
そしてこれはすなわち,
Precision = \frac{正しく(IoU ≥ 0.5)で検出できた数}{全ての予測BBoxの数}
Recall = \frac{正しく(IoU ≥ 0.5)で検出できた数}{全ての正解BBoxの数}
少し詳しく見ると,ここでは,
Precisionは,全ての予測結果(IoUに限らず全てのPredicted BBox)の内,正しくIoUが0.5以上で予測できた割合を表します.
Recallは,実際の正解結果(GT BBox)の内,IoUが0.5以上で正解結果とほぼ近しい位置のBBoxを予測できた割合を表します.
例を用いてPrecisionとRecallの計算例を示します.
この表2の例ではGT BBoxの数=5個だとして,
Sorted Numberが3番目の計算を例にとります.
表2."StopSign"と予測されたPredicted BBoxの検出結果(Precision,Recall)
| Sorted Number | Confidence Score(%) | Correct? | Precision | Recall |
|---|---|---|---|---|
| #1 | 96 | True | 1/1 = 1 | 1/5 = 0.2 |
| #2 | 92 | True | 2/2 = 1 | 2/5 = 0.4 |
| #3 | 89 | False | 2/3 = 0.667 | 2/5 = 0.4 |
| #4 | 88 | False | 2/4 = 0.5 | 2/5 = 0.4 |
| #5 | 84 | False | 2/5 = 0.4 | 2/5 = 0.4 |
| #6 | 83 | True | 3/6 = 0.5 | 3/5 = 0.6 |
| #7 | 80 | True | 4/7 = 0.571 | 4/5 = 0.8 |
| #8 | 78 | False | 4/8 = 0.5 | 4/5 = 0.8 |
| #9 | 74 | False | 4/9 = 0.444 | 4/5 = 0.8 |
| #10 | 72 | True | 5/10 = 0.5 | 5/5 = 1.0 |
このときこのソートされたBBox列の3番目におけるPrecisionは
Precision = \frac{それまで見てきたTrueの数}{それまで見てきたPredicted BBoxの総数} = 2/3 = 0.667
また,このソートされたBBox列の3番目におけるRecallは
Recall = \frac{それまで見てきたTrueの数}{全てのGT BBoxの数} = 2/5 = 0.4
のように計算できます.
5. AP, mAP
最後に,先ほど求めた物体検出のPrecisionとRecallを用いて,APとmAPを計算していきます.
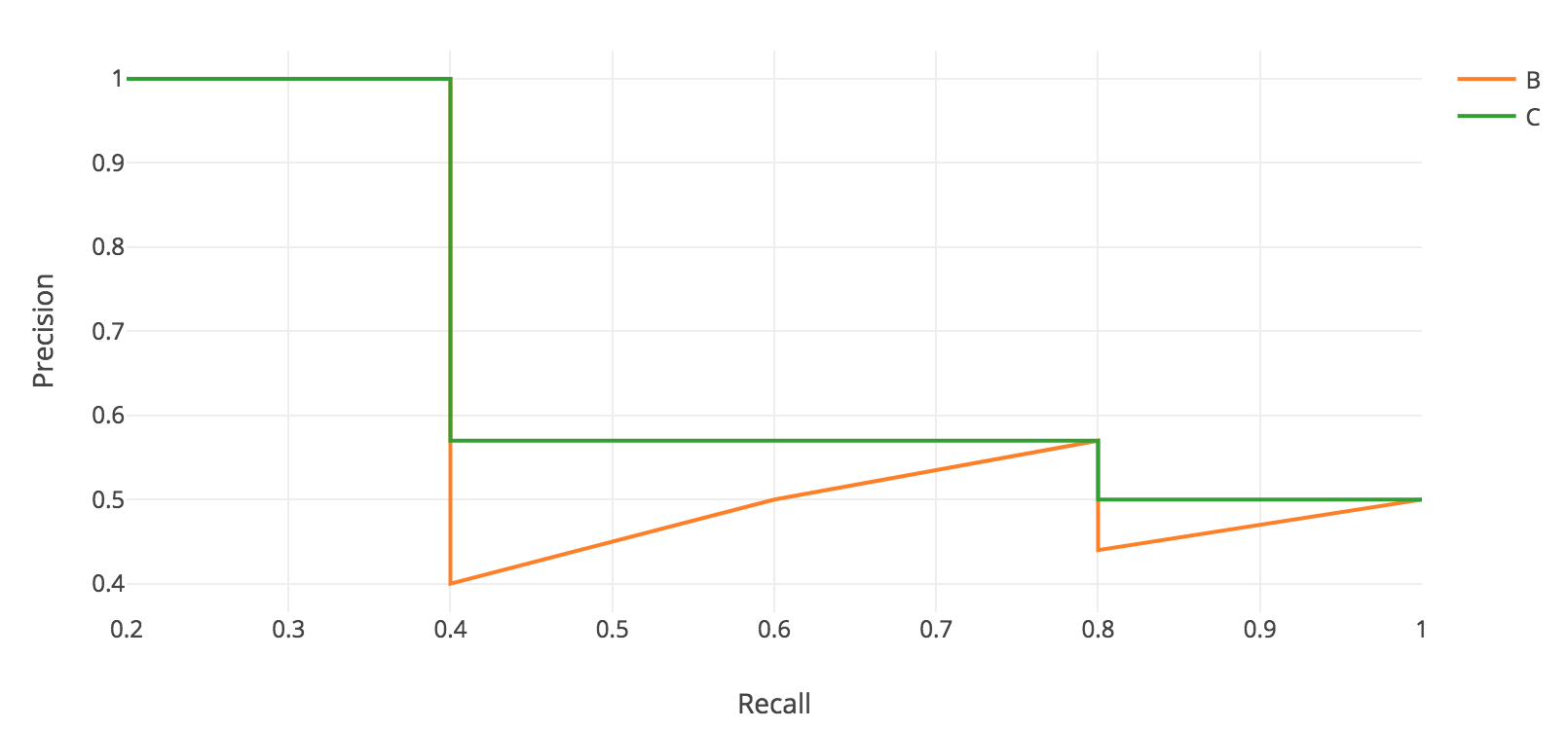
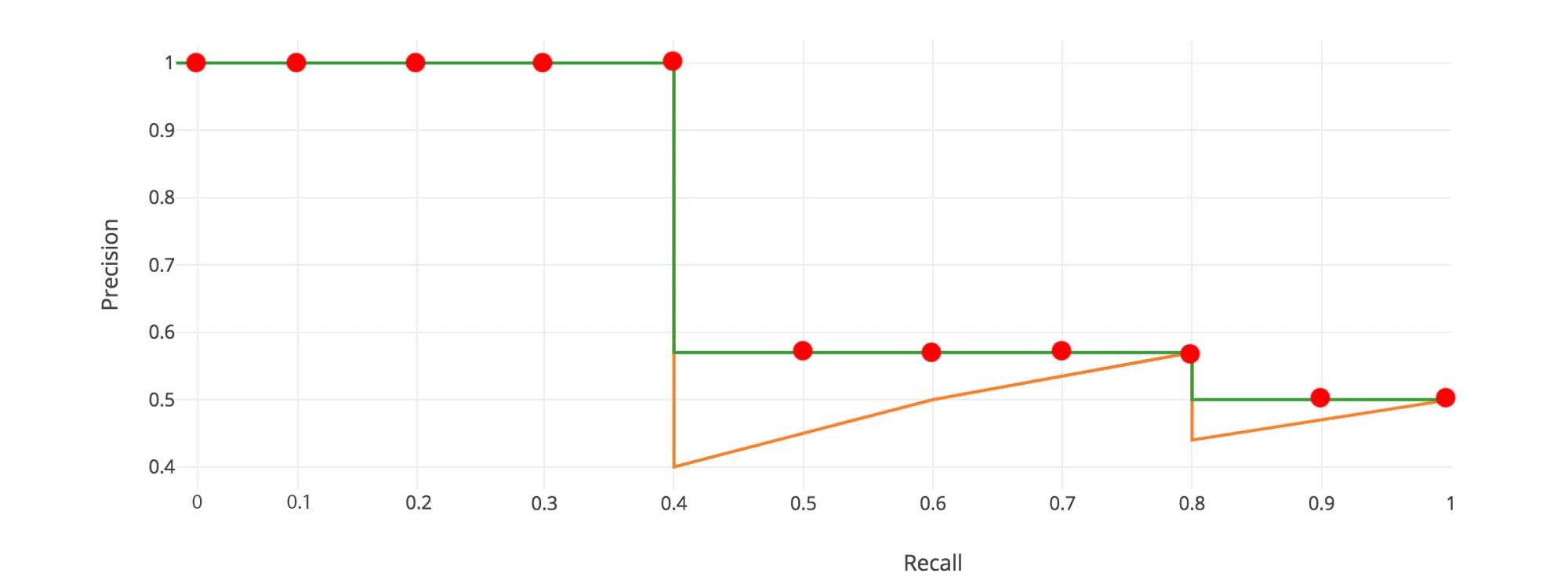
APを出すために,表2の結果のRecallを横軸,Precisionを縦軸にとり,グラフを描きます.
APは一般的に,
AP = \int_0^1 p(r) dr
のように積分を用いて表せます.
ここで,$p$はPrecisionの変数,$r$はRecallの変数です.
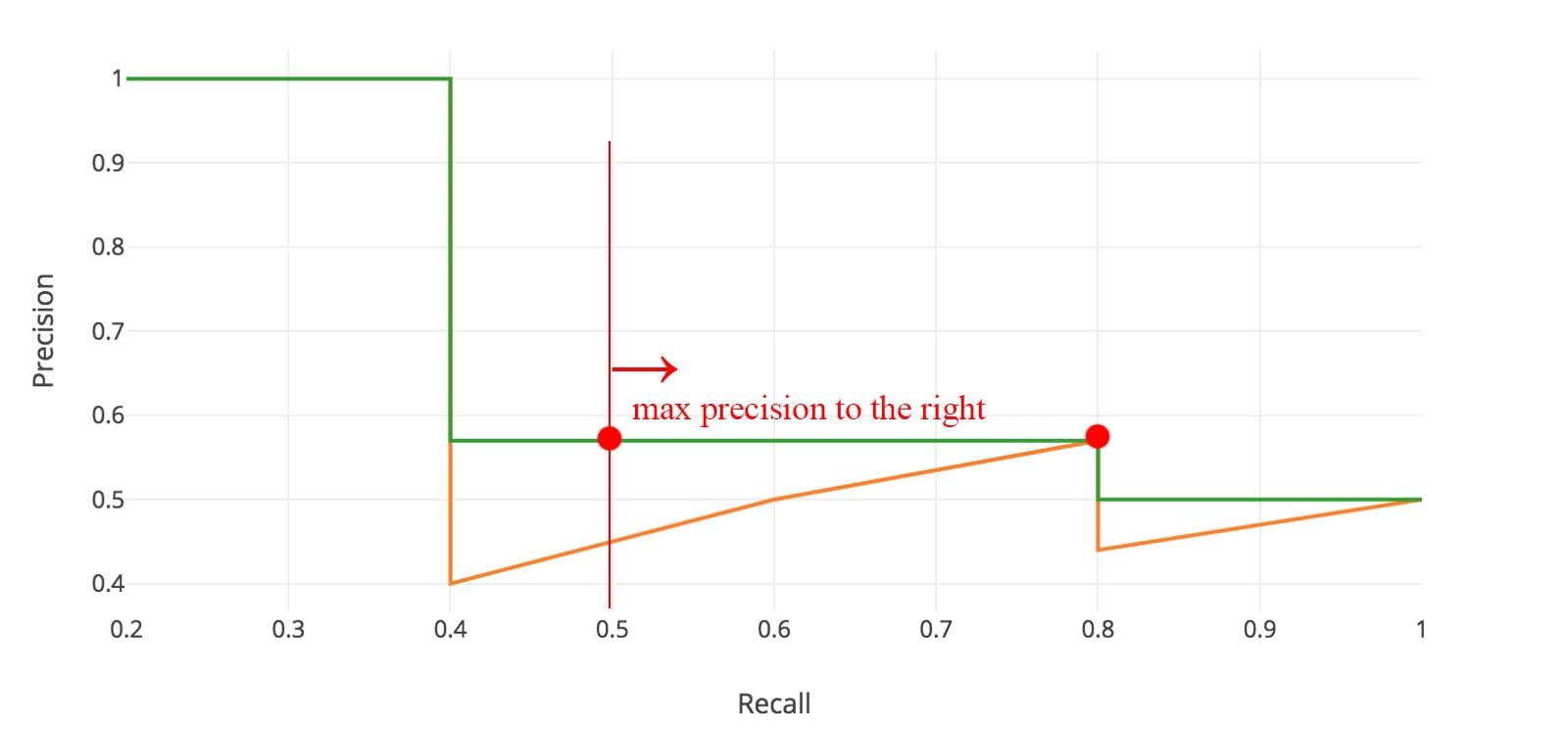
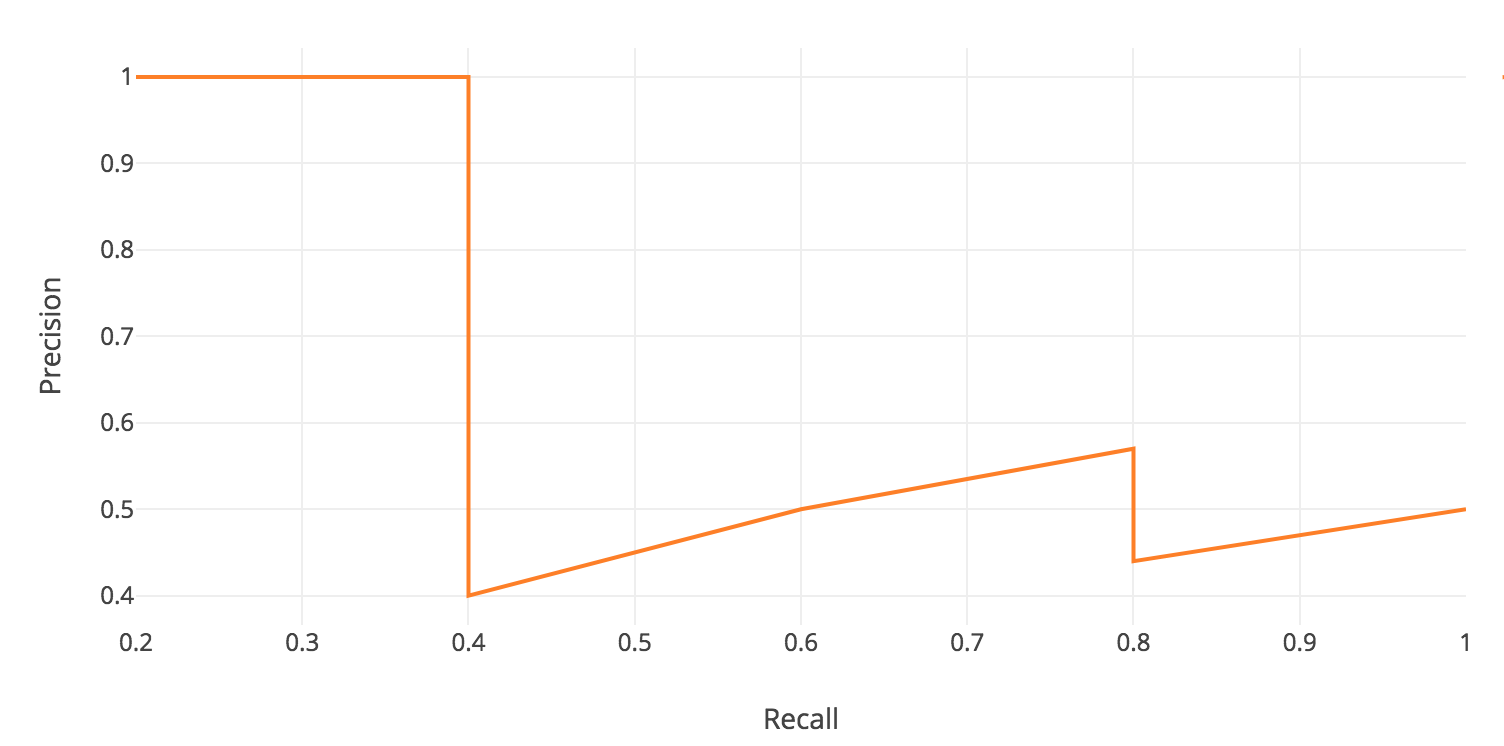
積分を行うために,上図のようにジグザグなパターンを滑らかにします.
具体的には,下図のように,各Recallのレベルで横に見た時に,Precisionの値が最大の値に置き換えます.
ここで原理的には通常の積分を行うのですが,
プログラム上で積分を行う際には,全ての点を扱うわけにはいかないので
この例のケースでは11点の代表点を取り,
APを求めるための積分として以下の計算を行います.
AP = \frac{1}{11}*(p(0) + p(0.1) + ・・・ + p(1.0))
AP = \frac{1}{11}*(1.0 * 5 + 0.571 * 4 + 0.5 * 2) = \frac{1}{11}*8.284 = 0.753
この手法は,物体検出のタスクの分野で有名なデータセットであるPASCAL VOCデータセットのAP算出でも用いられているものです.
これにより,"StopSign"のAP=0.753を得ることができました.
同様の方法で,**Label = ["StopSign", "TrafficLight", "Car"]**の3つ全てのクラスラベルのAPを以下のように算出できたとしましょう.
AP_{StopSign} = 0.753
AP_{TrafficLight} = 0.990
AP_{Car} = 0.683
この時のmAPは全てのクラスラベルのAPの平均を取れば良いので,
mAP = \frac{1}{3} * (0.753 + 0.990 + 0.683) = 0.8086
となり,最終的にこのモデルの$mAP=0.8086$(80.86%)という結果が得られました.(※論文などでは%表記で表示することが多いです.)
Mean Average Precisionの文字通り,APを全てのクラスについてさらに平均したものという訳ですね.
今回はIoU ≥ 0.5として説明を行いましたが,mAPを算出する際のこのIoUの閾値はもちろん任意に選択できます.
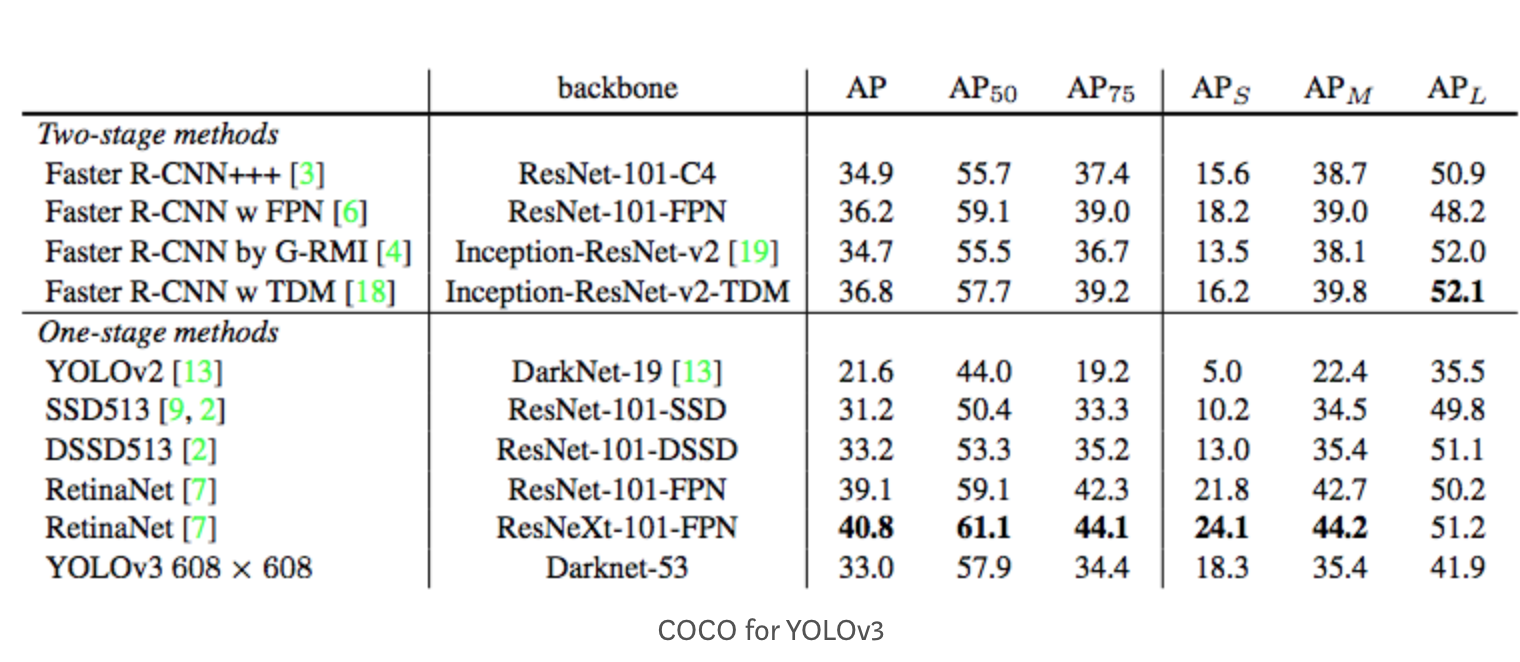
よく論文の表などで出てくる$AP_{50}$や$AP_{75}$などは実はmAPを計算する際のIoUの閾値を表しています.
IoUの閾値を上げるとその分TPの判定がシビアになるので,AP,mAPはその分低下する傾向にあることを覚えておいてください.
実装
実際に物体検出モデルでmAPを出したい場合はrafaelpadillaさんのGithubリポジトリを使います.
このリポジトリdは物体検出モデルの予測結果と正解データがあれば各AP値やRecall-Precisionのグラフも出力してくれるのでオススメです.
ただし「①物体検出モデルの予測結果を表す所定フォーマットのテキストファイル」と「②正解データを表す所定フォーマットのテキストファイル」が必要となります.
②についてはrafaelpadillaさんのGithubリポジトリで提供してあります.
しかし①については自分で実装して出力する必要があります.
①については私の方で作成し、私のgithubリポジトリに公開しました! (※)
皆さんも画像ごとのテキストファイルを吐き出した後、その結果をrafaelpadillaさんのGithubリポジトリで使用してmAPを計算することができますので、ご自身で物体検出モデルの精度を確かめて見てください.
これにて物体検出におけるmAPの算出方法についての説明を終わります.
間違いやご指摘などありましたら,コメント欄にて教えていただけるとうれしいです.
※追記:
大変申し訳ありませんが①についてメンテナンスが難しくなったため非公開とさせていただきました🙇
参考文献
-
Intersection over Union (IoU) for object detection
https://www.pyimagesearch.com/2016/11/07/intersection-over-union-iou-for-object-detection/ -
Medium: mAP (mean Average Precision) for Object Detection
https://medium.com/@jonathan_hui/map-mean-average-precision-for-object-detection-45c121a31173 -
Github: rafaelpadilla/Object-Detection-Metrics
https://github.com/rafaelpadilla/Object-Detection-Metrics#different-competitions-different-metrics -
物体検出で使われる評価指標 mAP について解説
https://pystyle.info/how-to-calculate-object-detection-metrics-map/#outline__4