AI.RL.LYsのcursheyです。
ロジスティック回帰モデル上のトンプソンサンプリングをバッチ学習で実装していたところ、処理速度が非常に遅くになってしまっていました。この原因の1つとして、多変量正規分布に従う重みをnumpy.random.multivariate_normalで取得していましたが、こちらの記事でこの関数は分散共分散行列が大きくなるほど遅く不安定であるという報告があり、このために処理が遅くなってしまっていると考えられます。
なので、今回の記事ではコレスキー分解を使って多変量正規分布を自前実装し、numpy.random.multivariate_normalをそのまま使う場合と、自前実装とでどのくらい速度が改善したかの検証結果について書きたいと思います。
なお、ロジスティック回帰モデル上のトンプソンサンプリングについての詳細な理論と実装方法については解説はしません。内容については「バンディット問題の理論とアルゴリズム」のp122~p125で確認をお願いします。また、この記事では速度改善のみに言及し、累積報酬やリグレット等によるトンプソンサンプリングの性能評価は行いません。
多変量正規分布生成の理論
多変量正規分布の生成は以下の定理を利用しています。
ある平均$\mu\in\mathbb{R}^n$と$n \times n$の分散共分散行列$\Sigma$に対して多変量正規分布$X\sim N(\mu,\Sigma)$とすると、$B\in\mathbb{R}^{n \times n}$が存在し以下の数式から標準正規分布$Z\sim N(0,1)$が得られる。
$$Z = B^{-1}(X-\mu)$$
最後の数式を以下のように変形することで多変量正規分布$X$を得ることができます。
$$
X = BZ + \mu
$$
この$B$ですが、これは分散共分散行列$\Sigma$を行列分解することで得ることができます。行列分解は特異値分解やコレスキー分解など様々な方法があります。numpy.random.multivariate_normalでは特異値分解を行なっていますが、分散共分散行列の次元数が大きくなるとこの処理が重くなってしまいます。コレスキー分解は特異値分解よりも比較的高速ですので、自前実装ではコレスキー分解を選択しました。ただ、どちらも計算量は$O(n^3)$ですので次元数の大きさは注意した方がいいです。
実際の実装
実際に実装する前に特異値分解とコレスキー分解の違いに注意したいです。特異値分解は行列が半正定値行列を条件にしていますが、コレスキー分解は正定値行列を条件にしています。分散共分散行列は定義から必ず半正定値行列にはなりますが正定値行列になる保証はありません。
また、今回はロジスティック回帰モデル上のトンプソンサンプリングをバッチ学習で実装しています。ロジスティック回帰モデル上のトンプソンサンプリングはMAP推定により分散共分散行列の更新をしますが、この更新はバッチ更新で行うため、重みの生成のたびに行列分解をする必要はありません。更新後の分散共分散行列を分解して使い回せば処理的に十分なので、行列分解を行う関数と多変量正規分布を取得する関数に分けました。実装は以下のようになります。
def get_decomposition_matrix(cov: np.array) -> (Tuple, str):
try:
return np.linalg.cholesky(cov), "cholesky"
except np.linalg.LinAlgError as e:
return np.linalg.svd(cov), "SVD"
def sample_multivariate_normal(mean: np.array, decomposition_matrix: Tuple,
decomposition: str) -> np.array:
if decomposition == "cholesky":
standard_normal_vector = np.random.standard_normal(len(decomposition_matrix))
return decomposition_matrix @ standard_normal_vector + mean
elif decomposition == "SVD":
u, s, vh = decomposition_matrix
standard_normal_vector = np.random.standard_normal(len(u))
return u @ np.diag(np.sqrt(s)) @ vh @ standard_normal_vector + mean
トンプソンサンプリングの擬似コード
numpy.random.multivariate_normalと、自前実装のコードをロジスティック回帰モデル上のトンプソンサンプリングに使った場合の擬似コードを紹介します、
まずはnumpy.random.multivariate_normalを使った場合の擬似コードです。
パラメータ: 平均ベクトル$\mu$, 分散共分散行列$\Sigma$を入力
- for $t = 1, 2, \cdots, T $ do
- $~~~~$乱数$\hat{\theta}$を
numpy.random.multivariate_normalに$\mu,\Sigma$を入力して生成- $~~~~$行動$i \leftarrow argmax_{i}~ a_{i, t}^T \hat{\theta}$を選択して報酬$X(t)$を観測
- $~~~~$if $t$が$\mu,\Sigma$の定期更新をする値になった時
- $~~~~~~~~$バッチ更新までの選択アームの特徴量と観測した報酬の軌跡からMAP推定をし、$\mu,\Sigma$を更新
- $~~~~$end if
- end for
次は自前実装のコードを使った場合の擬似コードです。
パラメータ: 平均ベクトル$\mu$, 分散共分散行列$\Sigma$を入力
- decomposition_matrix, decomposition = get_decomposition_matrix$(\Sigma)$
- for $t = 1, 2, \cdots, T $ do
- $~~~~$乱数$\hat{\theta}$ = sample_multivariate_normal($\mu$, decomposition_matrix, decomposition)
- $~~~~$行動$i \leftarrow argmax_{i}~ a_{i, t}^T \hat{\theta}$を選択して報酬$X(t)$を観測
- $~~~~$if $t$が$\mu,\Sigma$の定期更新をする値になった時
- $~~~~~~~~$バッチ更新までの選択アームの特徴量と観測した報酬の軌跡からMAP推定をし、$\mu,\Sigma$を更新
- $~~~~~~~~$decomposition_matrix, decomposition = get_decomposition_matrix$(\Sigma)$
- $~~~~$end if
- end for
実験1
トンプソンサンプリングを検証をした時の環境は、AWSのSageMaker上で以下のインスタンスタイプで実行しました。
- ノートブックインスタンスのタイプ: ml.t2.medium
実装したトンプソンサンプリングを検証する時の環境は以下のようにしました。
- アーム数: 1000
- 特徴量の次元数: 30
- バッチサイズ: 1000
- 共分散行列の初期値: 対角項のみで全ての値は0.1
- 平均ベクトルの初期値: 全て0
この環境下でタイムステップ数8000に対して、8回試行した時の平均を処理速度として計測しました。実験結果は以下の図のようになりました。

左の棒はnumpy.random.multivariate_normalを使ったもので、右の棒は自前実装をしたものです。自前実装の方が2倍程度処理速度が速いという結果が出ています。
実験2
トンプソンサンプリングを検証をした時の環境は、実験1と同様にAWSのSageMaker上で以下のインスタンスタイプで実行しました。
- ノートブックインスタンスのタイプ: ml.t2.medium
今回は特徴量の次元数を大きくした場合の検証です。その環境は以下のようにしました。
- アーム数: 1000
- 特徴量の次元数: 300
- バッチサイズ: 1000
- 共分散行列の初期値: 対角項のみで全ての値は0.1
- 平均ベクトルの初期値: 全て0
特徴量の次元数を30から300に増やしました。ここでもタイムステップ数8000に対して、8回試行した時の平均を処理速度として計測しました。実験結果は以下の図のようになりました。
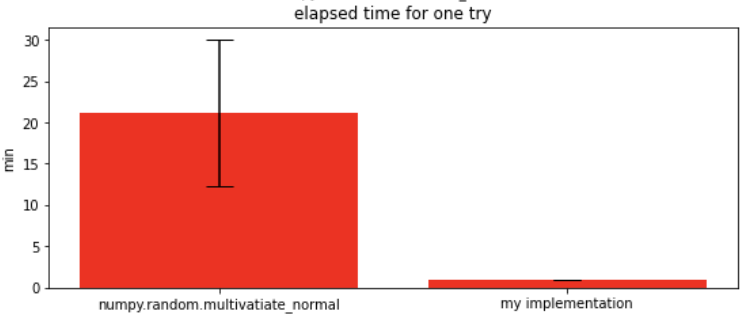
実験1と同様に左の棒はnumpy.random.multivariate_normalを使ったもので、右の棒は自前実装をしたものです。これを比較しますと、numpy.random.multivariate_normalに比べて自前実装の方は10倍程度の速度が出せていることがわかります。
検証結果まとめ
この速度改善をしたのはnumpy.random.multivariate_normalよりコレスキー分解を使った自前実装の方が処理速度が速く、特に特徴量の次元数が大きい場合にその影響が出てくるためと考えられます。
これだけでなく、行列分解を分散共分散行列の更新後のみにしているからと考えられます。numpy.random.multivariate_normalは分散共分散行列を特異値分解したものから多変量正規分布を生成しますが、分散共分散行列を更新しない限りは行列分解をする必要はありません。自前実装の方は行列分解と多変量正規分布を分けており、分散共分散行列の更新後のみ行列分解をし、分解後の行列を使いまわすことで不要な処理を減らすことができています。
以上をまとめますと、自前実装の方が速い理由は、
- 特異値分解よりコレスキー分解の方が速い
- 分散共分散行列の更新後しか行列分解を行わない
ということになると考えられます。