TODO
- 探索にも触れる
- 平衡を定義する
- 疑似コードを書く
概要
TODO
はじめに
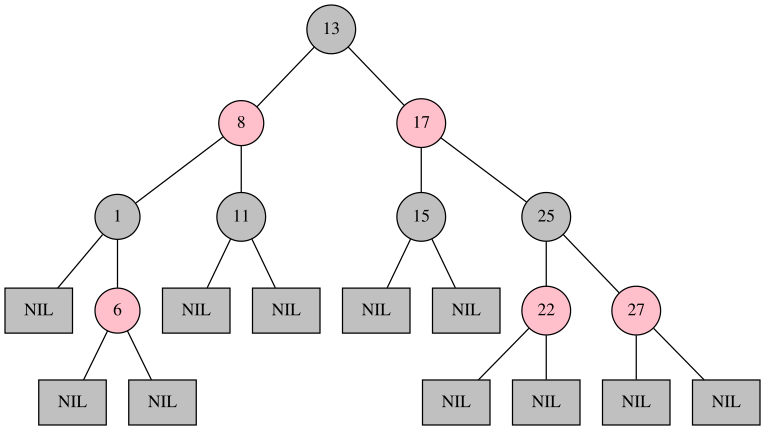
赤黒木は2分探索木の拡張である。
2分探索木はソート列(同じ要素はないものとする)を保持するデータ構造で、
左の子の値 < 自身の値 < 右の子の値
という順序制約を持った2分木である。
2分木には、左右の部分木の高さを平衡にする仕組みがない。
そのため、要素の挿入・削除の最悪時間計算量が大きくなる。
赤黒木は、各ノードを赤か黒に着色するというアイディアを基本に、
左右をある程度 平衡に保っている。
そのため、要素の挿入・削除の最悪時間計算量を $O(\log n)$ に抑えられる。
ここで、$n$ は要素数を示す。
この記事を書く理由は、
赤黒木はAVL木に並ぶ素晴らしいデータ構造であるにもかかわらず、
要素の挿入・削除について、日本語の分かりやすい資料が見つからなかったためである。
要素の挿入・削除については詳しく書くが、ソート列・2分探索木・AVL木・計算量・他の基本的なことは書かない。
赤黒木の基本についても簡単にしか書かない。
この記事は、赤黒木における要素の挿入と削除についてのものである。
2分探索木について
TODO
ソート列をもつデータ構造に2文探索木がある。
2文探索木の最悪時間計算量が $O(n)$ になので、
これを小さくするために平衡2文探索木というデータ構造がある。
平衡2文探索木にAVL木と赤黒木がある。
TODO AVL木と赤黒木を比較する
赤黒木とは
赤黒木は2分探索木に以下 5つの特徴を追加したデータ構造で、ソート列を保持するのに使われる。
5つの特徴を便宜上 性質3つ と 制約 2つに分ける。
TODO この段落 書き直し
5つの性質より、赤黒木は平衡になる。
具体的には、木の高さの最小値と最大値の比が2以下になる。
(木の高さが未定義)
性質(挿入・削除において意識する必要のない特徴)
- 各ノードは赤か黒の色を持つ。
- 根ノードは黒である。
- 全ての葉ノードは黒で、値 $NIL$ を持つ。
実装のときは、ノードではなく NULL ポインタで仮想的に扱うことが多い。
制約(挿入・削除において意識する必要のある特徴)
- 赤色ノードの子は黒色ノード、つまり赤ノード同士は親子にならない。
- 任意のノード $x$ から任意の葉ノード $l$ までの全てのパスは、同じ数の黒色ノードを持つ。
性質2について、根ノードが赤のときに黒に変えても、他の特徴を違反しないことに注意。
記法
制約の呼び方について、
制約1を赤制約、制約2を黒制約と呼ぶ。
ノードの呼び方について以下のようにする。
挿入削除について、考えるノードを $N$ とする。
$N$ の親ノードを $P$ とし、
$N$ が $P$ の右(左)の子であるとき、$N$ を右子(左子)と呼ぶ。
$P$ のもう一つの子ノード つまり $N$ の兄弟ノードを $S$ 、
$S$ の左の子ノードを $L$ 、 $S$ の右の子ノードを $R$ とする。
$P$ の親ノード つまり $N$ の祖父を $G$ 、
$G$ のもう一つの子ノード つまり $N$ の叔父ノードを $U$ とする。
ノードの色について、
ノード $X$ が赤のとき $X:R$ と書き、黒のとき $X:B$ と書く。
図中の部分木の表記について以下のようにする。
部分木を三角形で表す。
黒丸がついた三角形は、ついてない三角形よりも黒ノードの数が1つ多いことを示す。
部分木は、空集合のときもある。
操作と処理について。
回転操作と着色操作を合わせて操作と呼ぶ。
回転操作については参照文献を参照のこと。
以下ではいくつか場合分けが出てくるが、場合分けごとの一連の操作を処理と呼ぶことにする。
挿入と削除の概観
赤黒木の挿入削除は、2分探索木の挿入削除が参考になる。
赤黒木では、まず2分探索木と同じように要素の挿入削除を行い、
その後 制約を満たすように処理をしていく。
1つの処理のあと制約が満たされていれば完了し、
そうでない場合 再帰もしくは他の処理に移る。
挿入
2分探索木における挿入
2分探索木では、挿入するノード $N$ を根ノードから
順序制約に従って降ろし、$N$ を新しい葉ノードとする。
赤黒木における挿入
赤黒木では、挿入ノード $N$ を赤にし、
順序制約に従って下ろし、$N$ を新しく2つの NIL ノードを持つノードとする。
その後、下表の場合分けに従って処理していく。
ここで、赤ノードを挿入したとき、赤制約は違反しうるが、黒制約は違反しないことに注意。
挿入処理4,5 に関して、$P$ が左子の場合を説明する。$P$ が右子の場合は左右を逆にして考えること。
| 番号 | 場合分け | 処理 | 次 |
|---|---|---|---|
| 1 | $N$ が根ノード | 挿入処理1 | 完了 |
| 2 | $P:B$ | 挿入処理2 | 完了 |
| 3 | $P:R, U:R$ | 挿入処理3 | $G$ に対して再帰 |
| 4 | $P:R, U:B$ で $N$ が右子 | 挿入処理4 | 挿入処理5へ |
| 5 | $P:R, U:B$ で $N$ が左子 | 挿入処理5 | 完了 |
挿入処理1
$N$ が根ノード の場合
$N$ を黒にして完了。
挿入処理2
$P:B$ の場合
制約を違反しないので、完了。
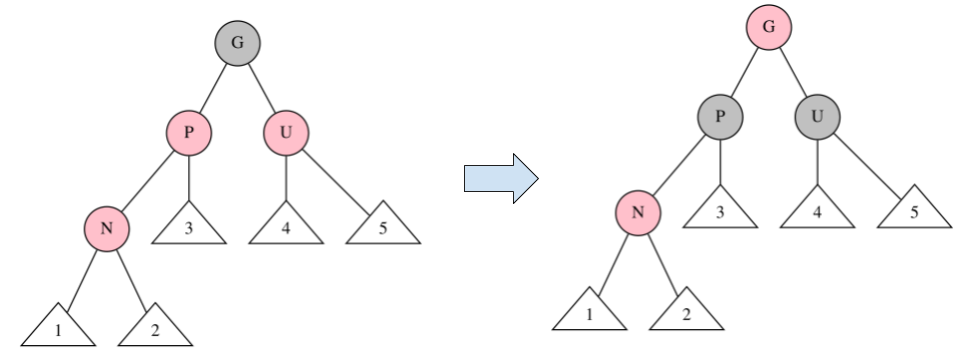
挿入処理3
$P:R, U:R$ の場合
図のように、$P, G, U$ の色を変える。
その後、$G$ を新しい $N$ として再帰。
上に再帰する (操作が上に移る) ので、処理回数は $O(\log n)$ になる。
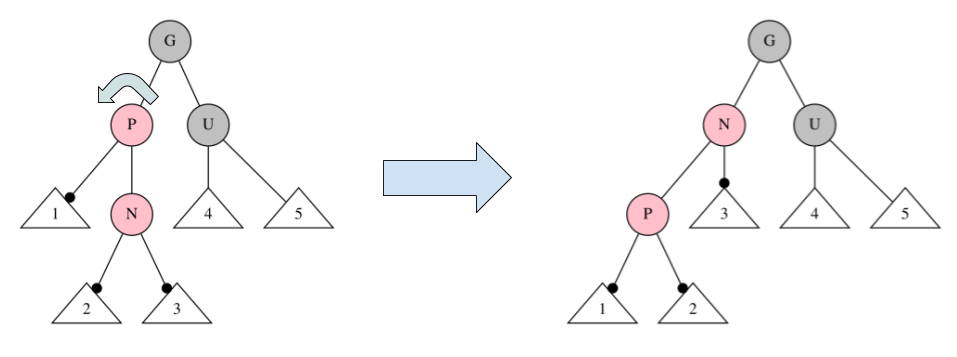
挿入処理4
$P:R, U:B$ で $N$ が右子 の場合
図のように、$P$ を左回転して挿入処理5へ。
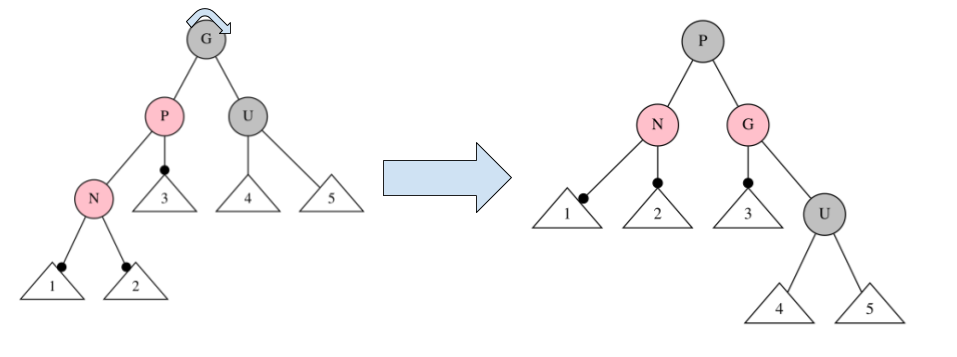
挿入処理5
$P:R, U:B$ で $N$ が左子 の場合
図のように、$G$ を右回転し、 $G, P$ の色を変更する。
削除
削除する対象のノードを $T$ とする。
また、$T$ の右の部分木のなかで最小値をもつノードを $M$ とする。
$T$ が右の部分木を持たない もしくは 右の子が $NIL$ のときは $M$ がないことに注意。
右の部分木のなかで最小値をもつノードを
左の部分木のなかで最大値をもつノードにしても議論は変わらない。
2分探索木における削除
2分探索木では、削除するノード $T$ を右の最小値ノード $M$ で置き換える。
そして、$M$ を削除して、$M$ の位置に $M$ の右の子を入れる。
ここで、$M$ は部分木の最小値なので、$M$ は左の子を持たないことに注意。
$T$ が右の子をもたない場合は、$T$ の左の子を $T$ に置き換える。
$T$ が葉ノードの場合は、$T$ を削除して完了。
赤黒木における削除
まず、$T$ の右の子が $NIL$ でない場合について、つまり $M$ が存在する場合について説明する。
$T$ の右の子が $NIL$ の場合は最後に説明する。
赤黒木では、削除するノード $T$ の色はそのままにして、値を $M$ の値で上書きする。
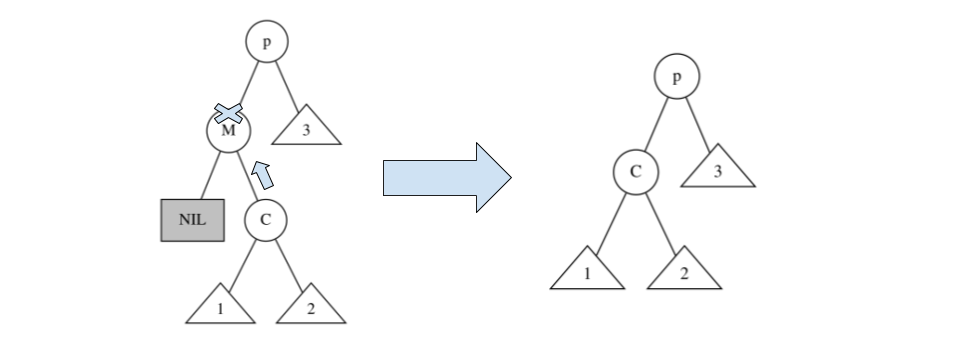
そして、下図のように $M$ を削除して、$M$ の位置に $M$ の右の子 $C$ を入れる
ここで、$M$ は部分木の最小値なので、$M$ の左の子は $NIL$ であることに注意。
図中では、$M$ の親ノードを $p$ としている。
$T$ まわりでは、色を保存しているので制約を違反しない。
$M$ まわりでは、制約を違反しうるので、場合分けしていく。
$M:R$ のとき、制約を違反しない。
$M:B, C:R$ のとき、$C:B$ とすればよい。
$M:B, C:B$ のときは複雑である。
以下、移動したあとの $C$ を $N$ と呼ぶことにして、説明していく。
$M:B, C:B$ のとき、
$N$ の兄弟ノード $S$ (つまり以前の $M$ の兄弟ノード) は $NIL$ でなく、子 $L$ と $R$ をもつ。
このことは、$N$ の親ノード $P$ (つまり以前の $M$ の親ノード) から見た黒制約を考えればわかる。
$M:B, C:B$ ということはつまり、$S$ から見て $M$ 側には 2つの黒ノードがあったということで、
黒制約に違反しないためには $S$ 側にも 2つの黒ノードが必要だからである。
今の状況を整理する。
$N:B$ で、$L, R$ が存在し、$P$ から見て $N$ 側の黒ノードが1つ少ない。
この黒制約に違反した状態を下表の場合分けに従って処理していくことで直していく。
表中で、 $A$ は赤でも黒でもよいことを、下線は赤制約により自然と決まることを示す。
また上に(下に)再帰とは、再帰処理が赤黒木の上に(下に)移ることを示す(削除処理4,5 の図を参照)。
| 番号 | 場合分け | 処理 | 次 |
|---|---|---|---|
| 1 | $P:R,\quad S:\underline B,\quad L:B,\quad R:B$ | 削除処理1 | 完了 |
| 2 | $P:A,\quad S:B,\quad L:A,\quad R:R$ | 削除処理2 | 完了 |
| 3 | $P:A,\quad S:B,\quad L:R,\quad R:B$ | 削除処理3 | 削除処理2 へ |
| 4 | $P:\underline B,\quad S:R,\quad L:\underline B,\quad R:\underline B$ | 削除処理4 | 下に再帰(削除処理4,5 にはならない) |
| 5 | $P:B,\quad S:B,\quad L:B,\quad R:B$ | 削除処理5 | 上に再帰 |
削除処理1
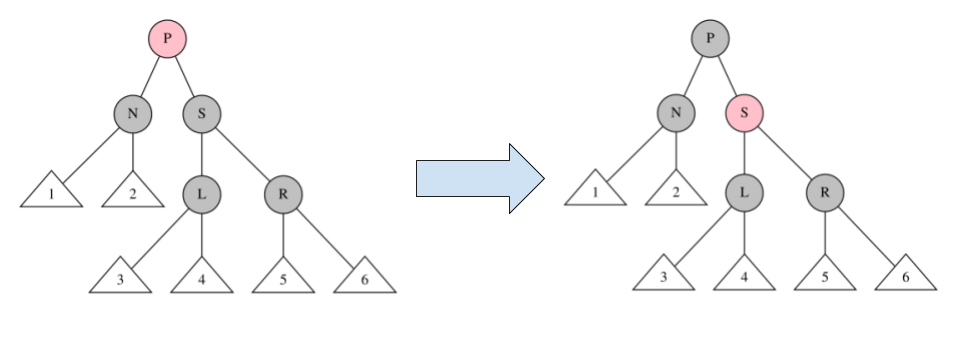
$P:R,\quad S:\underline B,\quad L:B,\quad R:B$ の場合、
下図のように、$P$ を黒に、$S$ を赤にする。
制約を満たすので、完了となる。
削除処理2
$P:A,\quad S:B,\quad L:A,\quad R:R$ の場合、
下図のように、$P$ で左回転して、$S$ を $P$ の色に、$P, R$ を黒にする。
制約を満たすので、完了となる。
削除処理3
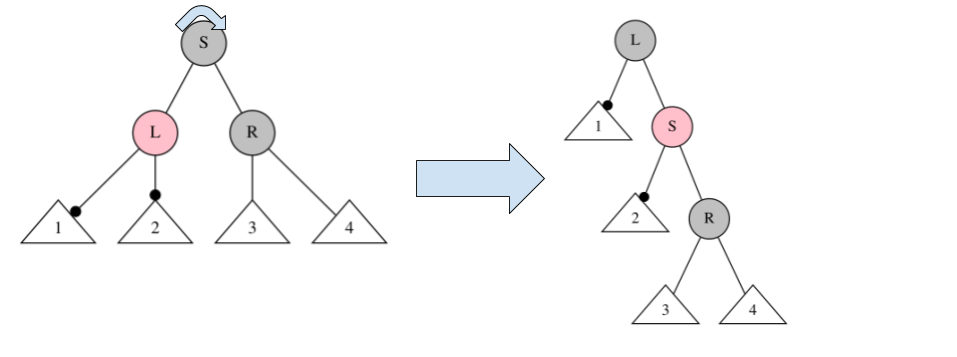
$P:A,\quad S:B,\quad L:R,\quad R:B$ の場合、
下図のように、$S$ を右回転して、$L, S$ の色を変えれば、削除処理2 を実行できる。
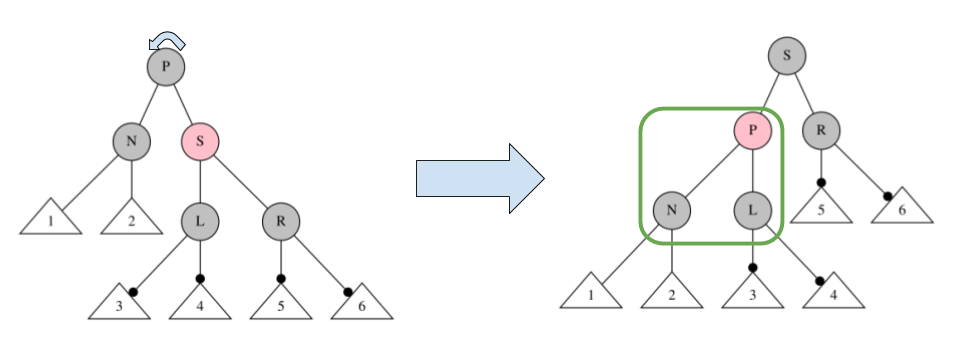
削除処理4
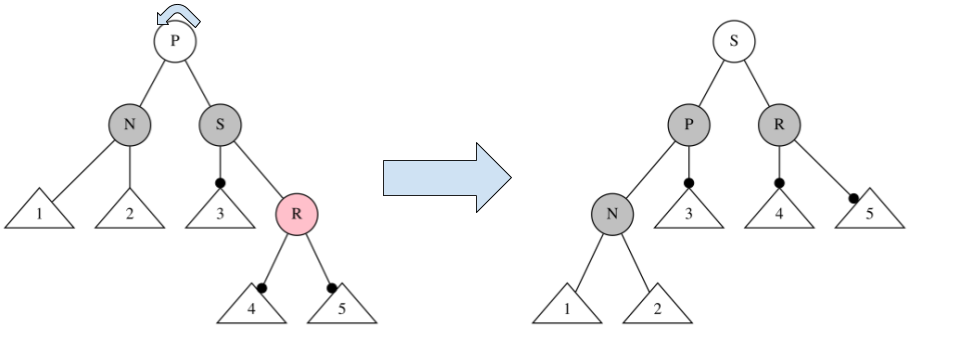
$P:\underline B,\quad S:R,\quad L:\underline B,\quad R:\underline B$ の場合、
下図のように、$P$ を左回転して、$P, S$ の色を変える。
その後、緑の箇所で再帰処理をする($L$ を新たな $S$ とする)。
場合分け4, 5 には当てはまらないので、以降の処理は定数回で完了する。
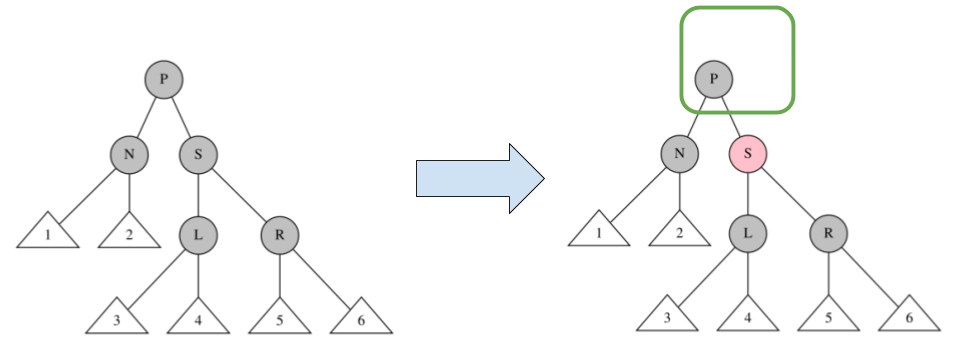
削除処理5
$P:B,\quad S:B,\quad L:B,\quad R:B$ の場合、
下図のように、$S$ を赤にする。
そうすると $P$ を通るパスで黒ノードが数が1つ減るので、
$P$ の親ノードから見て黒制約に違反する。
これを解消するために 緑の箇所で再帰処理をする($P$ を新たな $N$ とする)。
この再帰処理は常に上に移るので、以降の処理は $O(\log n)$ 回で完了する。
右の最小値ノードがない場合
$T$ の右の子が $NIL$ の場合について考える。
さらに 3つの場合分けがある。
- $T:R$ -> 完了。
- $T:B,\quad A:R$ -> 完了。
- $T:B,\quad A:B$ -> 上に再帰。
$T:R$ の場合、下図のように $T$ を削除すれば完了する。
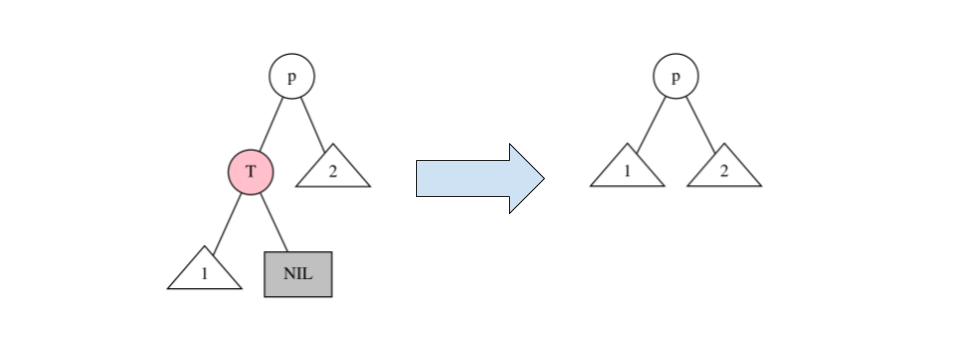
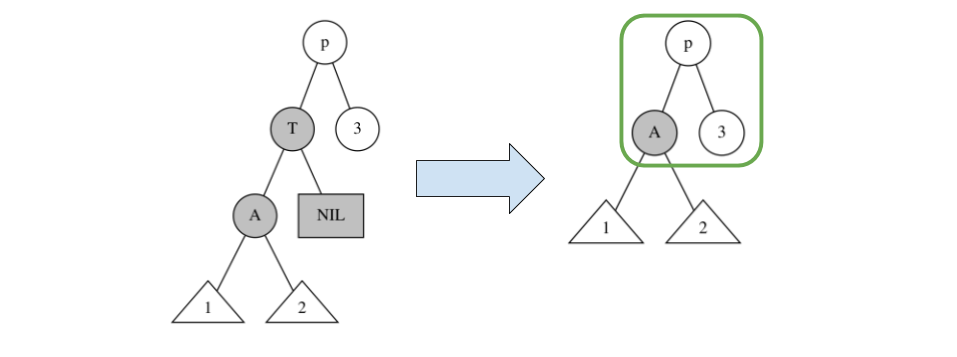
$T:B,\quad A:R$ の場合、下図のように $T$ を削除して、ノード $A$ を黒に変えれば完了する。
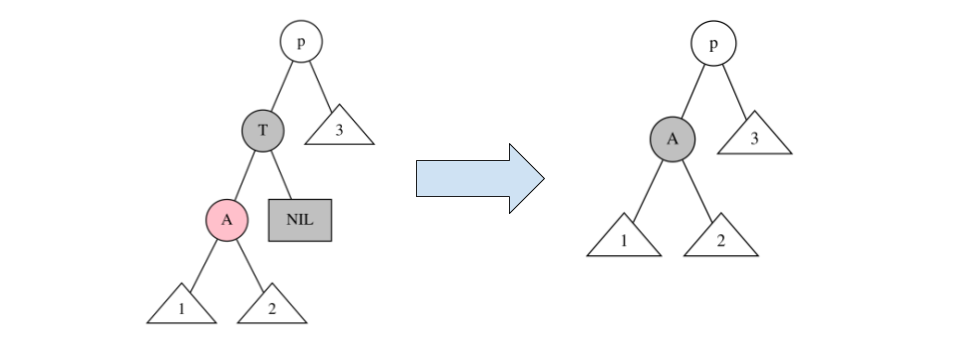
$T:B,\quad A:B$ の場合、下図のように $T$ を削除すると黒が1つ減り、黒制約に違反する。
そこで $A$ を $N$ として、$A$ を 新たな $N$ として緑の箇所で上述の削除処理を始める。
結文
赤黒木は場合分けが多くて難しいと思われがちだが、
場合分けを順に処理すれば個々は簡単である。
また、削除処理の計算量もうまく設計されており美しい。
この記事は参考文献の英語 wiki "red black tree" に依るところが大きい。
Thanks.
出典
wiki より
このデータ構造は1972年のルドルフ・ベイヤー (en:Rudolf Bayer) の発明である"symmetric binary B-trees"が元となっており、赤黒木という名前自体は 1978年にレオニダス・ギッバス (Leonidas J. Guibas) とロバート・セジウィック (en:Robert Sedgewick) によって発表された論文による。
参考文献
Rudolf Bayer (1972). "Symmetric binary B-Trees: Data structure and maintenance algorithms". Acta Informatica. 1 (4): 290–306. doi:10.1007/BF00289509.
Leonidas J. Guibas and Robert Sedgewick (1978). "A Dichromatic Framework for Balanced Trees". Proceedings of the 19th Annual Symposium on Foundations of Computer Science. pp. 8–21. doi:10.1109/SFCS.1978.3.
日本語 wiki: 木の回転
https://ja.wikipedia.org/wiki/%E6%9C%A8%E3%81%AE%E5%9B%9E%E8%BB%A2
eng wiki: red black tree
https://en.wikipedia.org/wiki/Red%E2%80%93black_tree
日本語 wiki: AVL tree
https://ja.wikipedia.org/wiki/AVL%E6%9C%A8