実関数の数値微分を複素関数で
藤井文夫, 田中真人, 佐藤維美『Fortran90/95による有限要素法プログラミング』(https://www.amazon.co.jp/dp/4621087843 )をパラパラ眺めていたところ、実数関数の数値微分の桁落ちによる誤差を避けるために、定義域を複素数に拡張して、虚軸側から数値微分する方法が載っていて興味を惹かれました。
真似て計算して見ます。
正則な複素関数の微分は複素平面のどの方向から近づいても同じ値に収束するので、正則関数ならこの方法が使えると思います。
計算結果
とりあえず、f(x) = sin(cos(x)) という、あんまり意味ない関数で試してみることにします。sin も cos もべき関数で定義されて正則なのでその合成関数も正則だったと思いますw
微分は df/dx = -sin(x) * cos(cos(x)) となりますので、この値と数値微分値を比較することにします。
x = 0.5 [ f(0.5)=0.769196354841008, f'(0.5)= -0.306358909189995] の地点で微係数を求めます。数値微分は微小値 h に対して:実数 (f(x+h)-f(x-h)) / (2h) , 複素数 (f(x+ih) - f(x-ih)) / i(2h) で計算します。
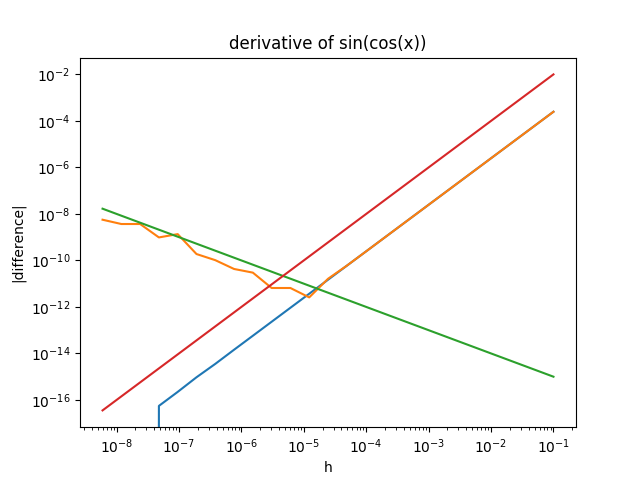
ここで図の横軸は数値微分のための微小値 h、縦軸は微分の理論値と数値微分値の差の絶対値です。グラフは log-log なので y= x^n 型のべき関数が直線になります。
図中の橙色の線が実数関数での数値微分、青線が複素関数での数値微分です。赤線は h^2 に比例する直線、緑線は 1/h に比例する直線です。
数値微分のオレンジと青は、微小値 h が小さくなるにつれて(図の右側から左側に行くにつれ)理論値との差が小さくなってゆきます。これは数値微分の打ち切り誤差に比例する項で、テイラー展開すればわかるように、h^2 に比例する誤差を持ちます。この理論値通りに h^2(赤線)比例して小さくなっています。
しかし、実数関数微分の方は途中から誤差が増え始めます。これは、f(x+h) と f(x-h) の値が同じくらいになって引き算による桁落ちが起きるためです。この誤差は有効数字の数に比例するので、橙色の線は左側の領域で 1/h(緑線)に比例する傾きを持っています。
一方、複素関数微分の方は、桁落ちを起こすことなくずっと h^2 に比例した誤差を持っています。確かに、複素関数で虚軸方向から数値微分すると、桁落ちによる誤差を避けることができました。
このまま調子に乗って、カットラインのある Log などで計算するか、微分でないけど超関数でも計算して見るかと思いましたが、雪かきで疲れたのでやめにします。
プログラム
数値微分は、x,h と微分される関数を関数引数として持つ関数を、実数と複素数の場合に定義して、それをさらに総称関数として束ねています。
注:Fortran の sin, cos などの組み込み関数は定義域が複素数になっています。(Fortran2003あたりからかな?ちょっと失念)
module m_mod
implicit none
integer, parameter :: kd = kind(0.0d0)
real(kd), parameter :: pi = 4 * atan(1.0_kd)
interface df
procedure :: df_r, df_c
end interface
interface
pure real(kd) function p_rf(x)
import
real(kd), intent(in) :: x
end function p_rf
pure complex(kd) function p_cf(z)
import
complex(kd), intent(in) :: z
end function p_cf
end interface
contains
pure real(kd) function rfunc(x)
real(kd), intent(in) :: x
rfunc = sin(cos(x))
end function rfunc
pure complex(kd) function zfunc(z)
complex(kd), intent(in) :: z
zfunc = sin(cos(z))
end function zfunc
pure elemental real(kd) function dfunc(x)
real(kd), intent(in) :: x
dfunc = -sin(x) * cos(cos(x))
end function dfunc
pure real(kd) function df_r(x, h, func)
real(kd), intent(in) :: x, h
procedure(p_rf) :: func
df_r = (func(x + h) - func(x - h)) / (2 * h)
end function df_r
pure real(kd) function df_c(x, h, func)
real(kd), intent(in) :: x, h
procedure(p_cf) :: func
complex(kd) :: c1, c0
c1 = cmplx(x, h, kind = kd)
c0 = cmplx(x,-h, kind = kd)
df_c = real( (func(c1) - func(c0)) / cmplx(0.0_kd, 2 * h, kind = kd) )
end function df_c
end module m_mod
program deriv
use m_mod
implicit none
integer, parameter :: n = 30
real(kd), parameter :: hh = 0.1_kd
real(kd) :: h(n), x, y1(n), y2(n), d
integer :: i
h = [(hh/2**i, i = 1, n)]
x = 0.5_kd
forall(i = 1:n) y1(i) = df(x, h(i), rfunc)
forall(i = 1:n) y2(i) = df(x, h(i), zfunc)
d = dfunc(x)
print *, " x f(x) f'(x)", x, rfunc(x), d
do i = 1, n
print *, 2 * h(i), d - y1(i), d - y2(i)
end do
end program deriv
計算値
x f(x) f'(x) 0.500000000000000 0.769196354841008
-0.306358909189995
0.100000000000000 2.471233679433027E-004 -2.479682338492051E-004
5.000000000000000E-002 6.186000401675606E-005 -6.191280813439004E-005
2.500000000000000E-002 1.546995069579005E-005 -1.547325095774266E-005
1.250000000000000E-002 3.867797066847700E-006 -3.868003329576819E-006
6.250000000000000E-003 9.669686005242539E-007 -9.669814948209954E-007
3.125000000000000E-003 2.417433517809542E-007 -2.417441650748309E-007
1.562500000000000E-003 6.043586719961525E-008 -6.043596573190868E-008
7.812500000000000E-004 1.510899605428051E-008 -1.510898672840710E-008
3.906250000000000E-004 3.777260504378432E-009 -3.777246349034868E-009
1.953125000000000E-004 9.444687254500650E-010 -9.443116288920805E-010
9.765625000000001E-005 2.356312922557890E-010 -2.360779349785957E-010
4.882812500000000E-005 5.941669378728420E-011 -5.901945598907332E-011
2.441406250000000E-005 1.621569545307011E-011 -1.475486399726833E-011
1.220703125000000E-005 2.573274926476188E-012 -3.688771510468314E-012
6.103515625000000E-006 -6.521672091253095E-012 -9.222067554048863E-013
3.051757812500000E-006 -6.521672091253095E-012 -2.305378110634138E-013
1.525878906250000E-006 2.985811597966403E-011 -5.762057497804562E-014
7.629394531250000E-007 -4.290146016217022E-011 -1.443289932012704E-014
3.814697265625000E-007 1.026176921214983E-010 -3.552713678800501E-015
1.907348632812500E-007 -1.884206124458387E-010 -9.436895709313831E-016
9.536743164062501E-008 -1.352573830715187E-009 -2.220446049250313E-016
4.768371582031250E-008 9.757326058235094E-010 -5.551115123125783E-017
2.384185791015625E-008 -3.680880267253883E-009 0.000000000000000E+000
1.192092895507813E-008 -3.680880267253883E-009 0.000000000000000E+000
5.960464477539063E-009 5.632345478900902E-009 0.000000000000000E+000
2.980232238769531E-009 -1.299410601340867E-008 0.000000000000000E+000
1.490116119384766E-009 2.425879697121047E-008 0.000000000000000E+000
7.450580596923829E-010 2.425879697121047E-008 0.000000000000000E+000
3.725290298461914E-010 2.425879697121047E-008 0.000000000000000E+000
1.862645149230957E-010 2.425879697121047E-008 0.000000000000000E+000
個人 memo 帳 お絵かき命令
title("derivative of sin(cos(x))")
xlabel("h")
ylabel("|difference|")
loglog(x[1:25],y3[1:25], x[1:25], y4[1:25], x[1:25], 1.0e-16 ./ x[1:25], x[1:25], x[1:25].^2)
savefig("deriv.png")