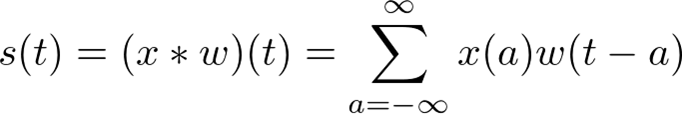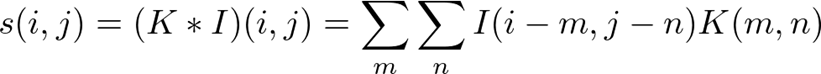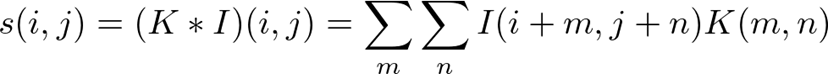Goodfellow Deep Learning 9.1~9.3

はじめに

9章について

• 畳み込みネットワーク(LeCun, 1989)
  • 畳み込みニューラルネットワーク(CNNs)とも呼ばれる
  • 「畳み込み」という数学的処理を利用
  • 少なくとも１つの層で畳み込みを利用するネットワーク
• 畳み込みネットワークが提供するいくつかのツールについて説明
  • 畳み込みネットワークの構造を選択する方法については１１章で説明

9章の構成

• 畳み込みについて
• 畳み込みを利用する理由
• プーリング
• 畳み込み関数のバリエーション
• 次元の異なるデータに適用する方法
• 効率的に畳み込みを行う方法
• 神経科学的な原理について
• 深層学習の歴史における役割

9.1 畳み込み処理

畳み込みとは

• 実数の引数を2つ持つ関数に対する処理
  

  • 1つ目の引数(関数x)は入力
  • 2つ目の引数(関数w) はカーネル
  • 出力は特徴マップ

• アスタリスク記号を使って表記
  

離散畳み込み

• 離散データに対する畳み込み
  

• 機械学習の応用では入力はデータの多次元配列，カーネルはパラメータの多次元配列となる

  • 値を格納する有限個の集合以外ではゼロであると考えることで，無限個の要素の総和を有限個の配列要素の総和として実現できる

二次元畳み込み

• ２つの軸に対する畳み込み
  

• 畳み込みの可換性（上記の式と以下の式は等価）
  

  • カーネルのインデックスが入力に対して反転していることから可換性が生じる
  • ニューラルネットワークの実装においては重要な性質ではない
  • ニューラルネットワークでは代わりに相互相関を用いる

相互相関

• 相互相関
  • 畳み込みと同様の処理だが，カーネル反転を行わない
  • 多くの機械学習ライブラリでは相互相関を実装し，それを　畳み込みと呼んでいる

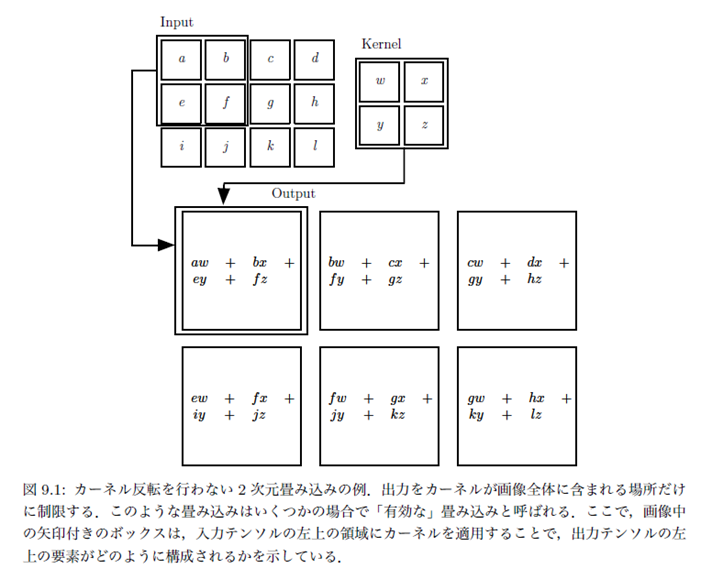
畳み込み処理の例

離散畳み込みと行列の積

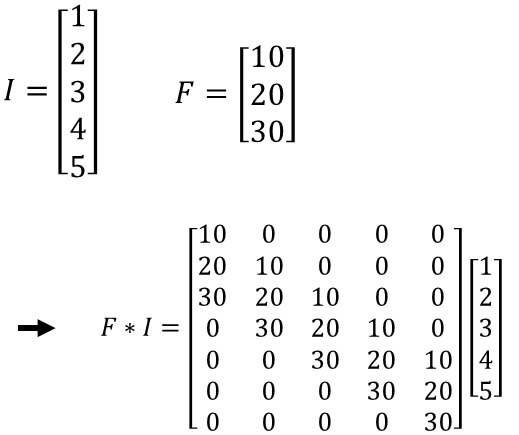
• 離散畳み込みは行列の掛け算とみなすことができる
• 行列は以下の２つの制約を持つ
  • いくつかの要素はその他の要素と一致する
  • 非常にスパースな(多くの要素がゼロである)行列である(一般にカーネルは入力画像よりもはるかに小さいため)
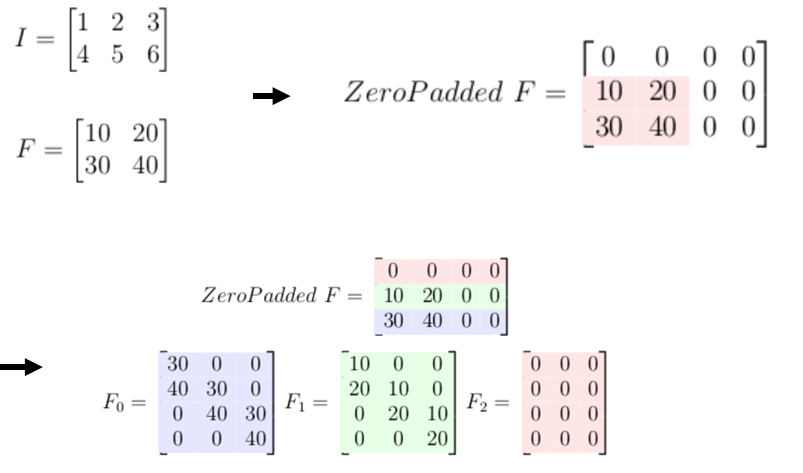
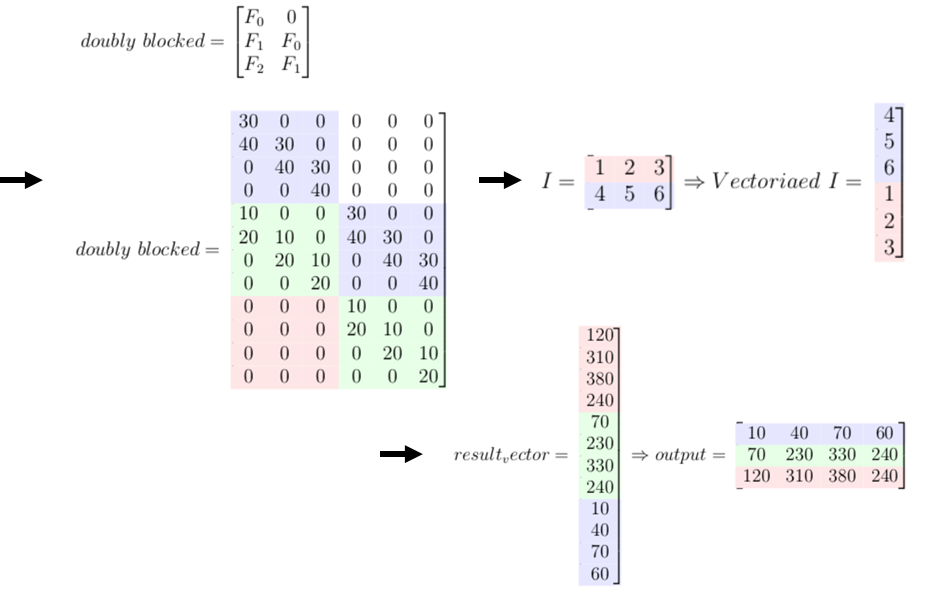
• １次元の場合はテプリッツ行列，２次元の場合は二重循環行列が畳み込みに対応

テプリッツ行列

二重循環行列

9.2 モチベーション

畳み込みのモチベーション

• 畳み込みは以下の３つの考え方をうまく利用している
  • 疎な結合
  • パラメータ共有
  • 等価表現

疎な結合

• 伝統的なニューラルネットワークは，出力ユニットすべてが入力ユニットすべてから影響を受ける
• 一方で畳み込みネットワークは疎な結合を利用
  • 入力より小さなカーネルを利用することで実現
  • 数千~数百万の入力に対し，カーネルは数十~数百程度
• 保管するパラメータの数を減らすことが可能
• 計算処理を減らすことが可能
  • 入力がm個，出力がn個の全結合の場合の計算量はO(m×n)
  • 出力がk個の結合を持つように制限すると計算量はO(k×n)
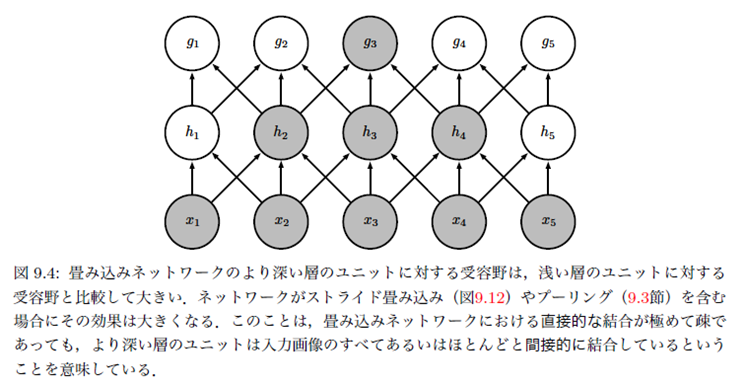
• 下側層から見た疎な結合
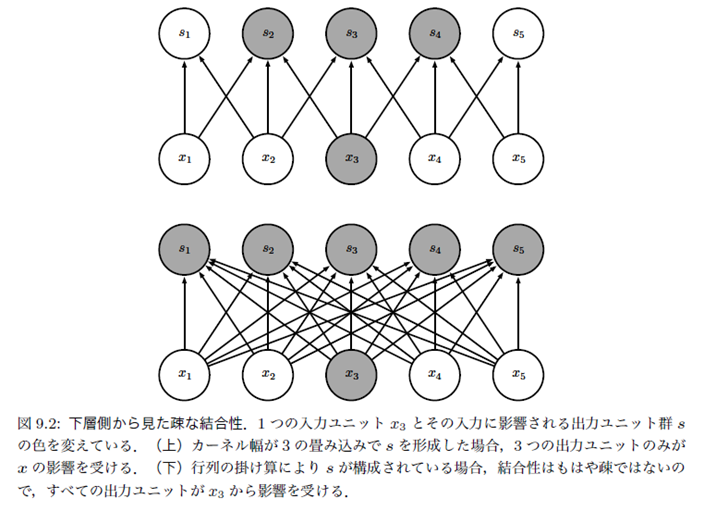
• 上側層から見た疎な結合
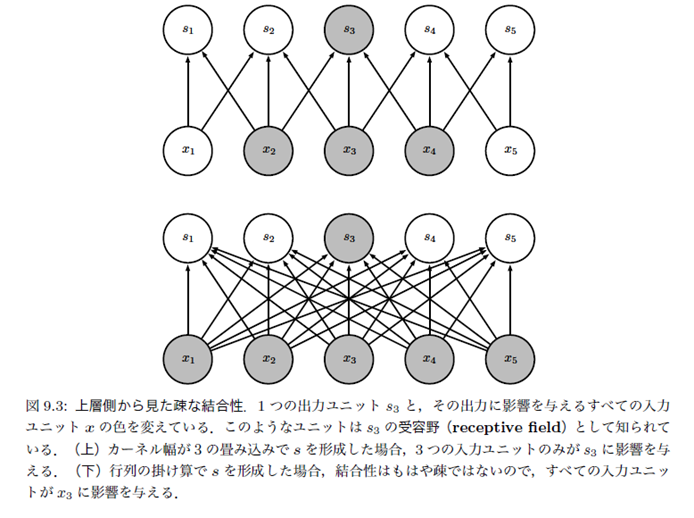
• 深い層のユニットは間接的に多くの入力と相互作用
  • 畳み込みは多くの変数の間の相互作用を効率的に表現する

パラメータ共有

• 伝統的なニューラルネットワークではある層の出力を計算するときの重み行列の各要素は一度だけ使われる
• 一方で畳み込みのカーネルの要素は入力の全ての位置で利用される(パラメータ共有)
• モデルの保存に必要なメモリ容量を低減する
  • 入力m個，出力n個の全結合に必要なメモリ容量はm×n
  • カーネルサイズkの畳み込みに必要なメモリ容量はk
• パラメータ共有の例

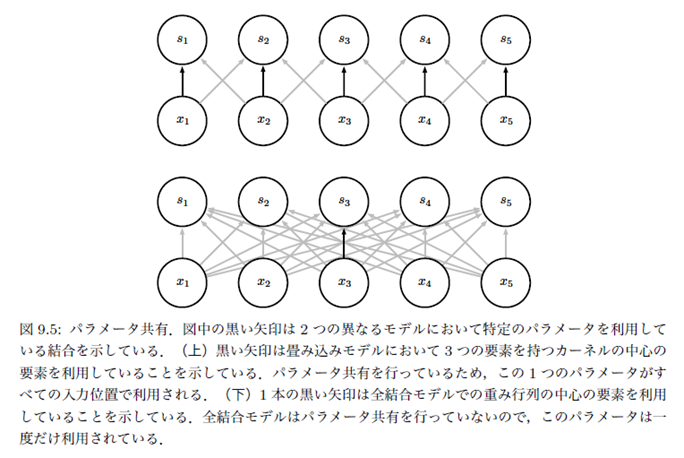
等価性

• ある関数が等価であるとは，入力が変化した場合に出力が同じように変化すること
• 入力をシフトしたものに畳み込みを適用した結果は，入力に畳み込みを適用したものをシフトした結果と一致
  • パラメータ共有によりこの性質を持つ
• 近接する少数のピクセルの関数を，複数の入力位置に　適用することが役立つと知っているときに等価性は有用
  • エッジ検出など(エッジは画像中のほとんどの場所に現れるため)
• 畳み込みは画像のスケーリングや回転などの変換に対しては等価ではない

9.3 プーリング

プーリング関数

• ある場所でのネットワークの出力を，周辺の出力の要約統計量で置き換える関数
  • 最大プーリング処理では矩形の近傍中の最大の出力を返す
  • その他に矩形近傍の平均値，L2ノルム，中心からの距離に基づく重み付き平均など
• 入力の小さな移動に対してほぼ不変な表現を作るときに役立つ
  • 入力を多少変化させてもプーリング後のほとんどの出力値は変化しない
• 画像中のある特徴の厳密な位置より，画像中にその特徴が存在するかどうかに関心がある場合に有用

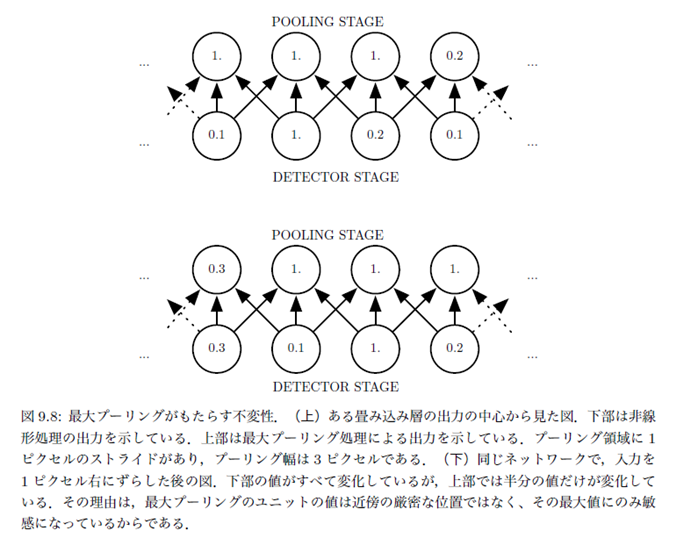
最大プーリングと不変性

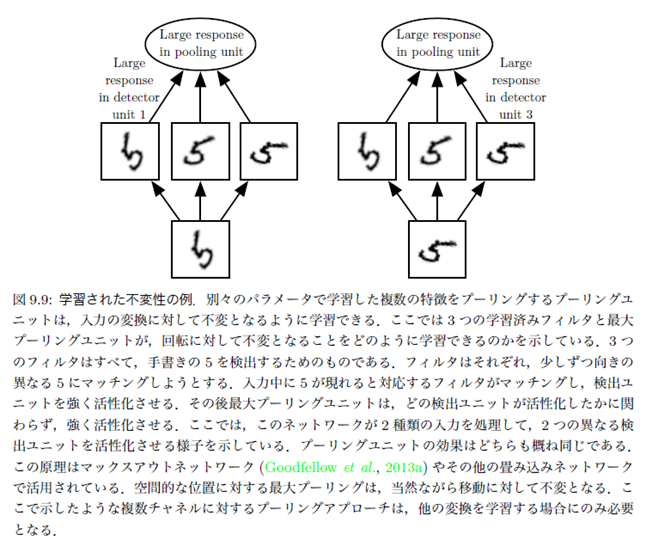
プーリングによる不変性の学習

• 個々にパラメータ化された畳み込みの出力に対してプーリングを行った場合，どの変換に対して不変に　なるかを学習できる

計算効率の向上とメモリ削減

• １ピクセルごとではなくkピクセルごとにプーリングを行うことで，次の層で処理する入力数は 1 / k になる
• これにより計算効率の向上とパラメータ保持に必要なメモリの削減につながる

可変サイズ入力に対するプーリング

• 多くのタスクにおいて，プーリングは可変サイズの入力を扱う上で欠かせない
• 可変サイズの画像を分類するときに分類層への入力サイズは固定でなければならない
• 入力のサイズに応じてプーリング領域間オフセットのサイズを変更することで，分類層が常に同じ数の入力を受け取るようにする

プーリングの応用

• いくつかの理論的な研究では，どの種類のプーリングをどのような場面で利用するべきかの指針が提供されている(Boureau et al, 2010)
• 興味深い特徴の場所においてクラスタリングアルゴリズムを実行し，特徴量をまとめて動的にプーリングすることが可能(Boureau et al, 2011)
  • この方法では画像ごとに異なるプーリング領域が生まれる
• プーリング構造を１つだけ学習し，それを全画像に適応するというアプローチもある(Jia et al, 2012)

参考文献

• Deep Learning
  • Ian Goodfellow, Yoshua Bengio, Aaron Courville
  • 日本語版