Python実装 混合ベルヌーイ分布

PRML9.3.3の混合ベルヌーイ分布を実装していきます。EMアルゴリズムの例としては、ガウス分布をいくつか足し合わせた混合ガウス分布の最尤推定が一般的ですが、ベルヌーイ分布を足し合わせた混合ベルヌーイ分布の最尤推定にも適用可能です。ガウス分布には平均と分散の２種類のパラメータがあるのに対して、ベルヌーイ分布のパラメータは一種類だけなのでむしろこちらのほうが簡単です。
今回は混合ベルヌーイ分布を使って、PRMLのようにMNISTに適用させて各数字ごとにクラスタリングします。

混合ベルヌーイ分布

今回用いるモデルは多次元ベルヌーイ分布をもとにしています。これはD次元のニ値ベクトルの分布を表しています。

{\rm Bern}({\bf x}|{\bf\mu}) = \prod_{i=1}^D \mu_i^{x_i}(1-\mu_i)^{(1-x_i)}

これをK次元の混合係数${\bf\pi}$で重み付けしてK個足し合わせたものが混合ベルヌーイ分布となります。学習データを${\bf X}=\{{\bf x}_1,\dots,{\bf x}_N\}$とすると、

p({\bf X}|{\bf\mu},{\bf\pi}) = \prod_{n=1}^N\left\{\sum_{k=1}^K\pi_k{\rm Bern}({\bf x}_n|{\bf\mu}_k)\right\}

となる。ここで個々のデータに対して潜在変数${\bf Z}=\{{\bf z}_1,\dots,{\bf z}_N\}$を導入します。K次元のニ値潜在変数ベクトル${\bf z}$はK個の成分のうち一つだけ1となり、それ以外の成分は全て0となっている。完全データ${\bf X,Z}$が与えられたときの尤度関数は次のようになる。

p({\bf X, Z}|{\bf\mu,\pi}) = \prod_{n=1}^N\left\{\prod_{k=1}^K\pi_k^{z_{nk}}{\rm Bern}({\bf x}_n|{\bf\mu}_k)^{z_{nk}}\right\}

コード

import

多次元ベルヌーイ分布をそのまま用いると尤度が小さすぎて計算機では不都合があるので、対数を用いるためにlogsumexpを使う

import numpy as np
from scipy.misc import logsumexp

混合ベルヌーイ分布

python2系の人は@をnumpyの内積を計算する関数に適宜入れ替えてください。

# 混合ベルヌーイ分布
class BernoulliMixtureDistribution(object):

    def __init__(self, n_components):
        # クラスタ数
        self.n_components = n_components

    def fit(self, X, iter_max=100):
        self.ndim = np.size(X, 1)

        # パラメータの初期化
        self.weights = np.ones(self.n_components) / self.n_components
        self.means = np.random.uniform(0.25, 0.75, size=(self.n_components, self.ndim))
        self.means /= np.sum(self.means, axis=-1, keepdims=True)

        # EMステップを繰り返す
        for i in range(iter_max):
            params = np.hstack((self.weights.ravel(), self.means.ravel()))

            # Eステップ
            stats = self._expectation(X)

            # Mステップ
            self._maximization(X, stats)
            if np.allclose(params, np.hstack((self.weights.ravel(), self.means.ravel()))):
                break
        self.n_iter = i + 1

    # PRML式(9.52)の対数
    def _log_bernoulli(self, X):
        np.clip(self.means, 1e-10, 1 - 1e-10, out=self.means)
        return np.sum(X[:, None, :] * np.log(self.means) + (1 - X[:, None, :]) * np.log(1 - self.means), axis=-1)

    def _expectation(self, X):
        # PRML式(9.56)
        log_resps = np.log(self.weights) + self._log_bernoulli(X)
        log_resps -= logsumexp(log_resps, axis=-1)[:, None]
        resps = np.exp(log_resps)
        return resps

    def _maximization(self, X, resps):
        # PRML式(9.57)
        Nk = np.sum(resps, axis=0)

        # PRML式(9.60)
        self.weights = Nk / len(X)

        # PRML式(9.58)
        self.means = (X.T @ resps / Nk).T

結果

このjupyter notebook 9.3.3のように混合ベルヌーイ分布をMNISTデータセット（から0~4の画像をそれぞれランダムに200枚とってきたもの）に適用すると、個々のベルヌーイ分布の平均は下の図のようになりました。

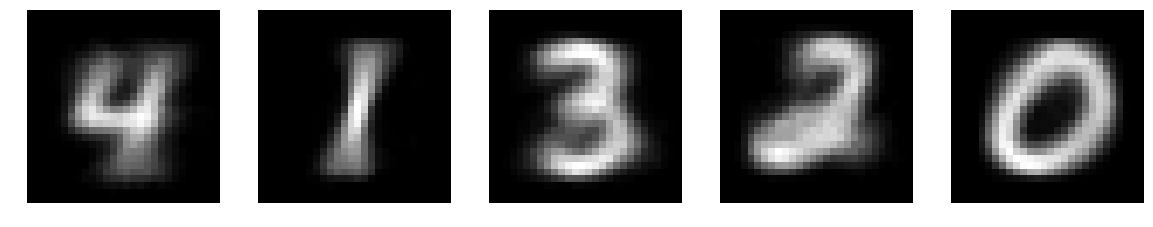
終わりに

EMアルゴリズムの学習は局所解（本当は局所解じゃないのかもしれないけど）にはまるので上のように綺麗にそれぞれの数字が映ることばかりではありません。体感的には、1と7や3と8のように形状に類似点があるペアがあると学習がうまく行きにくかったように思いました。