今回はマルコフ連鎖モンテカルロ(MCMC)の代表例であるメトロポリスアルゴリズムを実装しました。ガウス分布や一様分布などの有名な確率分布だけでなく、もっと形が複雑な分布からもサンプリングしたいときによく用いられる手法です。
メトロポリスアルゴリズム
ある確率分布$p(x)={1\over Z_p}\tilde{p}(x)$からサンプリングすることを考えます。規格化定数$Z_p$は分からなくても構いません。ベイズの定理とかで確率分布を求めるときに規格化定数が分からないことがよくあります。
分かっているのは規格化されていない関数$\tilde{p}(\cdot)$だけなのでここから直接サンプリングはできません。そこで提案分布と呼ばれる直接サンプリングできる別の確率分布(例えば、ガウス分布)を用意します。ただし、提案分布は対称なものとします。
メトロポリス法の流れ
- 初期値$x_1$を設定
- $x_i$を中心とした提案分布からサンプル候補一つ($x^*$)をサンプルする
- $\min(1, {\tilde{p}(x^*)\over\tilde{p}(x_i)})$の確率で$x_{i+1}=x^*$とし、受理されなかったら$x_{i+1}=x_i$とする
- ステップ2、3を繰り返して得られた系列$\{x_n\}_{n=1}^N$を確率分布$p(x)$からのサンプルとする
という非常にシンプルな手法です。
この手順で得られたサンプル系列はその前後のサンプルと非常に強い相関があります。サンプリングでは独立なサンプルが欲しいことが多いので、サンプル系列のうちM個ごとのサンプルだけを保持することで相関が弱まります。
コード
ライブラリ
matplotlibとnumpyを使用します
import matplotlib.pyplot as plt
import numpy as np
メトロポリス法
class Metropolis(object):
def __init__(self, func, ndim, proposal_std=1., sample_rate=1):
# 規格化されていない関数
self.func = func
# データの次元
self.ndim = ndim
# 提案分布(ガウス分布)の標準偏差
self.proposal_std = proposal_std
# サンプルを間引く
self.sample_rate = sample_rate
# サンプリング
def __call__(self, sample_size):
# 初期値の設定
x = np.zeros(self.ndim)
# サンプルを保持するリスト
samples = []
for i in xrange(sample_size * self.sample_rate):
# 提案分布からサンプリング
x_new = np.random.normal(scale=self.proposal_std, size=self.ndim)
x_new += x
# PRML式(11.33) サンプル候補が受理される確率を計算
accept_prob = self.func(x_new) / self.func(x)
if accept_prob > np.random.uniform():
x = x_new
# サンプルを保持
if i % self.sample_rate == 0:
samples.append(x)
return np.array(samples)
メイン関数
def main():
# 規格化されていない関数
def func(x):
return np.exp(-0.5 * np.sum(x ** 2, axis=-1) / 5.)
# まず一次元空間で試す
print "one dimensional"
# 提案分布の標準偏差を2、サンプルを10個ごとに間引く
sampler = Metropolis(func, ndim=1, proposal_std=2., sample_rate=10)
# メトロポリス法を使って100個サンプリング
samples = sampler(sample_size=100)
# サンプル平均と分散を確認
print "mean", np.mean(samples)
print "var", np.var(samples, ddof=1)
# サンプル結果を図示
x = np.linspace(-10, 10, 100)[:, None]
y = func(x) / np.sqrt(2 * np.pi * 5.)
plt.plot(x, y, label="probability density function")
plt.hist(samples, normed=True, alpha=0.5, label="normalized sample histogram")
plt.scatter(samples, np.random.normal(scale=0.001, size=len(samples)), label="samples")
plt.xlim(-10, 10)
plt.show()
# 次は二次元空間で試す
print "\ntwo dimensional"
sampler = Metropolis(func, 2, proposal_std=2., sample_rate=10)
samples = sampler(sample_size=100)
print "mean\n", np.mean(samples, axis=0)
print "covariance\n", np.cov(samples, rowvar=False)
x, y = np.meshgrid(
np.linspace(-10, 10, 100), np.linspace(-10, 10, 100))
z = func(np.array([x, y]).reshape(2, -1).T).reshape(100, 100)
plt.contour(x, y, z)
plt.scatter(samples[:, 0], samples[:, 1])
plt.xlim(-10, 10)
plt.ylim(-10, 10)
plt.show()
コード全体
import matplotlib.pyplot as plt
import numpy as np
class Metropolis(object):
def __init__(self, func, ndim, proposal_std=1., sample_rate=1):
self.func = func
self.ndim = ndim
self.proposal_std = proposal_std
self.sample_rate = sample_rate
def __call__(self, sample_size):
x = np.zeros(self.ndim)
samples = []
for i in xrange(sample_size * self.sample_rate):
x_new = np.random.normal(scale=self.proposal_std, size=self.ndim)
x_new += x
accept_prob = self.func(x_new) / self.func(x)
if accept_prob > np.random.uniform():
x = x_new
if i % self.sample_rate == 0:
samples.append(x)
assert len(samples) == sample_size
return np.array(samples)
def main():
def func(x):
return np.exp(-0.5 * np.sum(x ** 2, axis=-1) / 5.)
print "one dimensional"
sampler = Metropolis(func, ndim=1, proposal_std=2., sample_rate=10)
samples = sampler(sample_size=100)
print "mean", np.mean(samples)
print "var", np.var(samples, ddof=1)
x = np.linspace(-10, 10, 100)[:, None]
y = func(x) / np.sqrt(2 * np.pi * 5.)
plt.plot(x, y, label="probability density function")
plt.hist(samples, normed=True, alpha=0.5, label="normalized sample histogram")
plt.scatter(samples, np.random.normal(scale=0.001, size=len(samples)), label="samples")
plt.xlim(-10, 10)
plt.show()
print "\ntwo dimensional"
sampler = Metropolis(func, 2, proposal_std=2., sample_rate=10)
samples = sampler(sample_size=100)
print "mean\n", np.mean(samples, axis=0)
print "covariance\n", np.cov(samples, rowvar=False)
x, y = np.meshgrid(
np.linspace(-10, 10, 100), np.linspace(-10, 10, 100))
z = func(np.array([x, y]).reshape(2, -1).T).reshape(100, 100)
plt.contour(x, y, z)
plt.scatter(samples[:, 0], samples[:, 1])
plt.xlim(-10, 10)
plt.ylim(-10, 10)
plt.show()
if __name__ == '__main__':
main()
結果
下の図はそれぞれ一次元、二次元空間でサンプルした結果を表しています。
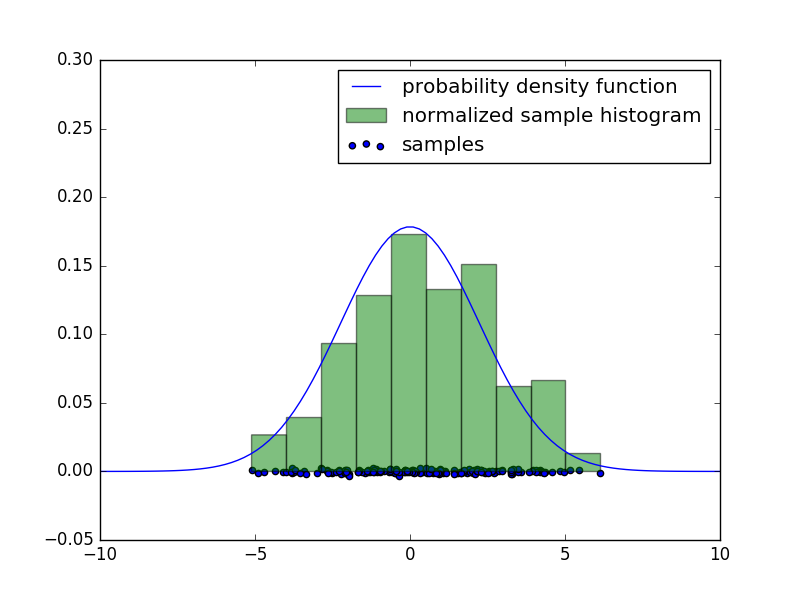
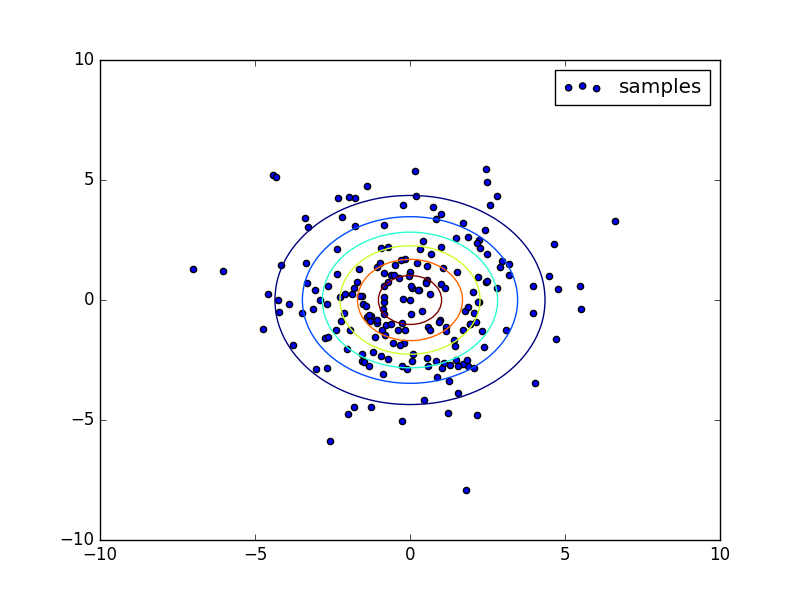
等高線は確率密度関数のものです。
ターミナルの出力結果
one dimensional
mean 0.427558835137
var 5.48086205252
two dimensional
mean
[-0.04893427 -0.04494551]
covariance
[[ 5.02950816 -0.02217824]
[-0.02217824 5.43658538]]
[Finished in 1.8s]
サンプル平均と分散がどちらの場合もそれぞれ母平均と母分散に近い値となっています。
終わりに
他にもハミルトニアンモンテカルロなどの手法もあるので、機会があればそれらも実装していきます。