PRML第10章 変分混合ガウス分布 Python実装

今回は前回の記事の最後に言っていた変分混合ガウス分布を実装しました。前回はEMアルゴリズムを用いて混合ガウス分布のパラメータを最尤推定しましたが、今回は変分ベイズ法を使って混合ガウス分布のパラメータをベイズ推定します。前回の実装では混合ガウス分布の混合要素数をこちらが設定していましたが、変分ベイズ法を用いることで自動的に混合要素数を決定してくれます。他にもベイズ的に扱う利点がいくつかあります。

変分混合ガウス分布

通常の混合ガウス分布の最尤推定では混合係数$\pi_k$、平均$\mu_k$、共分散$\Sigma_k$（もしくは精度$\Lambda_k$）を最尤推定しましたが、今回はそれら全てが確率変数だとしてその確率分布を推定します。

今回用いるモデルをグラフィカルモデルにしたものが下の図（PRML図10.5より抜粋）です。

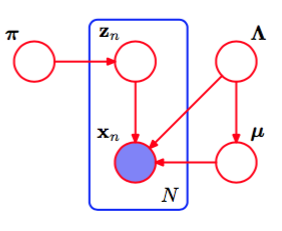
これらの確率変数全ての同時分布は

p({\bf X}, {\bf Z}, {\bf \pi}, {\bf \mu}, {\bf \Lambda}) = p({\bf X}|{\bf Z},{\bf\mu},{\bf\Lambda})p({\bf Z}|{\bf\pi})p({\bf\pi})p({\bf\mu}|{\bf\Lambda})p({\bf\Lambda})

となります。

今回の変分ベイズ法の要は、${\bf X}$を観測した後の事後分布$p({\bf Z}, {\bf \pi}, {\bf \mu}, {\bf \Lambda}|{\bf X})$を次のように潜在変数${\bf Z}$とパラメータに分解した確率分布に変分近似していることです。

\begin{align}
p({\bf Z}, {\bf \pi}, {\bf \mu}, {\bf \Lambda}|{\bf X}) &\approx q({\bf Z}, {\bf \pi}, {\bf \mu}, {\bf \Lambda})\\
&= q({\bf Z})q({\bf\pi},{\bf\mu},{\bf\Lambda})
\end{align}

元の事後分布を厳密に計算することは困難なので変分近似を用いています。

今回の変分ベイズ法の大まかな流れは
1. 確率分布$q({\bf Z})$と$q({\bf\pi},{\bf\mu},{\bf\Lambda})$を初期化
2. $q({\bf Z})$を更新（EMアルゴリズムのEステップに相当する）
3. $q({\bf\pi},{\bf\mu},{\bf\Lambda})$を更新（EMアルゴリズムのMステップに相当する）
4. 収束するまでステップ２、３を繰り返す
のようになっています。ステップ２、３の数式を書き下すと相当な量になってしまうので、割愛します。

コード

ライブラリ

いつも通りのmatplotlibとnumpyに加えてscipyも使っています。ディガンマ関数とガンマ関数が必要なので、今回はアルゴリズムの部分でもNumpy以外のライブラリを使います。

import matplotlib.cm as cm
import matplotlib.pyplot as plt
import numpy as np
from scipy.special import digamma, gamma

変分混合ガウス

class VariationalGaussianMixture(object):

    def __init__(self, n_component=10, alpha0=1.):

        # 混合ガウス分布の混合要素数
        self.n_component = n_component

        # 混合係数piの事前分布のパラメータ
        self.alpha0 = alpha0

    def init_params(self, X):
        self.sample_size, self.ndim = X.shape

        # 事前分布のパラメータを設定
        self.alpha0 = np.ones(self.n_component) * self.alpha0
        self.m0 = np.zeros(self.ndim)
        self.W0 = np.eye(self.ndim)
        self.nu0 = self.ndim
        self.beta0 = 1.

        self.component_size = self.sample_size / self.n_component + np.zeros(self.n_component)

        # 確率分布のパラメータを初期化
        self.alpha = self.alpha0 + self.component_size
        self.beta = self.beta0 + self.component_size
        indices = np.random.choice(self.sample_size, self.n_component, replace=False)
        self.m = X[indices].T
        self.W = np.tile(self.W0, (self.n_component, 1, 1)).T
        self.nu = self.nu0 + self.component_size

    # 確率分布のパラメータを返す
    def get_params(self):
        return self.alpha, self.beta, self.m, self.W, self.nu

    # 変分ベイズ法
    def fit(self, X, iter_max=100):
        self.init_params(X)

        # 確率分布が収束するまで更新する
        for i in xrange(iter_max):
            params = np.hstack([array.flatten() for array in self.get_params()])

            # 確率分布q(z)の更新
            r = self.e_like_step(X)

            # 確率分布q(pi, mu, Lambda)の更新
            self.m_like_step(X, r)

            # 収束していれば終了
            if np.allclose(params, np.hstack([array.ravel() for array in self.get_params()])):
                break
        else:
            print("parameters may not have converged")

    # 確率分布q(z)の更新
    def e_like_step(self, X):
        d = X[:, :, None] - self.m
        gauss = np.exp(
            -0.5 * self.ndim / self.beta
            - 0.5 * self.nu * np.sum(
                np.einsum('ijk,njk->nik', self.W, d) * d,
                axis=1)
        )
        pi = np.exp(digamma(self.alpha) - digamma(self.alpha.sum()))
        Lambda = np.exp(digamma(self.nu - np.arange(self.ndim)[:, None]).sum(axis=0) + self.ndim * np.log(2) + np.linalg.slogdet(self.W.T)[1])

        # PRML式(10.67) 負担率の計算
        r = pi * np.sqrt(Lambda) * gauss

        # PRML式(10.49) 負担率を正規化
        r /= np.sum(r, axis=-1, keepdims=True)

        # 0割が生じた場合に備えて
        r[np.isnan(r)] = 1. / self.n_component
        return r

    # 確率分布q(pi, mu, Lambda)の更新
    def m_like_step(self, X, r):

        # PRML式(10.51)
        self.component_size = r.sum(axis=0)

        # PRML式(10.52)
        Xm = X.T.dot(r) / self.component_size

        d = X[:, :, None] - Xm
        # PRML式(10.53)
        S = np.einsum('nik,njk->ijk', d, r[:, None, :] * d) / self.component_size

        # PRML式(10.58) q(pi)のパラメータを更新
        self.alpha = self.alpha0 + self.component_size

        # PRML式(10.60)
        self.beta = self.beta0 + self.component_size

        # PRML式(10.61)
        self.m = (self.beta0 * self.m0[:, None] + self.component_size * Xm) / self.beta

        d = Xm - self.m0[:, None]
        # PRML式(10.62)
        self.W = np.linalg.inv(
            np.linalg.inv(self.W0)
            + (self.component_size * S).T
            + (self.beta0 * self.component_size * np.einsum('ik,jk->ijk', d, d) / (self.beta0 + self.component_size)).T).T

        # PRML式(10.63)
        self.nu = self.nu0 + self.component_size

    # p(テストデータ|トレーニングデータ)をpi,mu,Lambdaの推定値で近似
    def predict_proba(self, X):

        # PRML式(B.80) 精度行列Lambdaの期待値
        covs = self.nu * self.W
        precisions = np.linalg.inv(covs.T).T

        d = X[:, :, None] - self.m
        exponents = np.sum(np.einsum('nik,ijk->njk', d, precisions) * d, axis=1)
        # PRML式(10.38)
        gausses = np.exp(-0.5 * exponents) / np.sqrt(np.linalg.det(covs.T).T * (2 * np.pi) ** self.ndim)

        # PRML式(10.69) 混合係数piの期待値
        gausses *= (self.alpha0 + self.component_size) / (self.n_component * self.alpha0 + self.sample_size)

        # 潜在変数zについて周辺化
        return np.sum(gausses, axis=-1)

    # クラスタリング
    def classify(self, X):
        # 確率分布q(Z)のargmax
        return np.argmax(self.e_like_step(X), 1)

    # スチューデントのt分布を計算
    def student_t(self, X):
        nu = self.nu + 1 - self.ndim

        # PRML式(10.82)
        L = nu * self.beta * self.W / (1 + self.beta)

        d = X[:, :, None] - self.m
        # PRML式(B.72)
        maha_sq = np.sum(np.einsum('nik,ijk->njk', d, L) * d, axis=1)

        # PRML式(B.68)
        return (
            gamma(0.5 * (nu + self.ndim))
            * np.sqrt(np.linalg.det(L.T))
            * (1 + maha_sq / nu) ** (-0.5 * (nu + self.ndim))
            / (gamma(0.5 * nu) * (nu * np.pi) ** (0.5 * self.ndim)))

    # 予測分布p(テストデータ|トレーニングデータ)を計算
    def predict_dist(self, X):
        # PRML式(10.81)
        return (self.alpha * self.student_t(X)).sum(axis=-1) / self.alpha.sum()

全体のコード

import matplotlib.cm as cm
import matplotlib.pyplot as plt
import numpy as np
from scipy.special import digamma, gamma


class VariationalGaussianMixture(object):

    def __init__(self, n_component=10, alpha0=1.):
        self.n_component = n_component
        self.alpha0 = alpha0

    def init_params(self, X):
        self.sample_size, self.ndim = X.shape
        self.alpha0 = np.ones(self.n_component) * self.alpha0
        self.m0 = np.zeros(self.ndim)
        self.W0 = np.eye(self.ndim)
        self.nu0 = self.ndim
        self.beta0 = 1.

        self.component_size = self.sample_size / self.n_component + np.zeros(self.n_component)
        self.alpha = self.alpha0 + self.component_size
        self.beta = self.beta0 + self.component_size
        indices = np.random.choice(self.sample_size, self.n_component, replace=False)
        self.m = X[indices].T
        self.W = np.tile(self.W0, (self.n_component, 1, 1)).T
        self.nu = self.nu0 + self.component_size

    def get_params(self):
        return self.alpha, self.beta, self.m, self.W, self.nu

    def fit(self, X, iter_max=100):
        self.init_params(X)
        for i in xrange(iter_max):
            params = np.hstack([array.flatten() for array in self.get_params()])
            r = self.e_like_step(X)
            self.m_like_step(X, r)
            if np.allclose(params, np.hstack([array.ravel() for array in self.get_params()])):
                break
        else:
            print("parameters may not have converged")

    def e_like_step(self, X):
        d = X[:, :, None] - self.m
        gauss = np.exp(
            -0.5 * self.ndim / self.beta
            - 0.5 * self.nu * np.sum(
                np.einsum('ijk,njk->nik', self.W, d) * d,
                axis=1)
        )
        pi = np.exp(digamma(self.alpha) - digamma(self.alpha.sum()))
        Lambda = np.exp(digamma(self.nu - np.arange(self.ndim)[:, None]).sum(axis=0) + self.ndim * np.log(2) + np.linalg.slogdet(self.W.T)[1])
        r = pi * np.sqrt(Lambda) * gauss
        r /= np.sum(r, axis=-1, keepdims=True)
        r[np.isnan(r)] = 1. / self.n_component
        return r

    def m_like_step(self, X, r):
        self.component_size = r.sum(axis=0)
        Xm = X.T.dot(r) / self.component_size
        d = X[:, :, None] - Xm
        S = np.einsum('nik,njk->ijk', d, r[:, None, :] * d) / self.component_size
        self.alpha = self.alpha0 + self.component_size
        self.beta = self.beta0 + self.component_size
        self.m = (self.beta0 * self.m0[:, None] + self.component_size * Xm) / self.beta
        d = Xm - self.m0[:, None]
        self.W = np.linalg.inv(
            np.linalg.inv(self.W0)
            + (self.component_size * S).T
            + (self.beta0 * self.component_size * np.einsum('ik,jk->ijk', d, d) / (self.beta0 + self.component_size)).T).T
        self.nu = self.nu0 + self.component_size

    def predict_proba(self, X):
        covs = self.nu * self.W
        precisions = np.linalg.inv(covs.T).T
        d = X[:, :, None] - self.m
        exponents = np.sum(np.einsum('nik,ijk->njk', d, precisions) * d, axis=1)
        gausses = np.exp(-0.5 * exponents) / np.sqrt(np.linalg.det(covs.T).T * (2 * np.pi) ** self.ndim)
        gausses *= (self.alpha0 + self.component_size) / (self.n_component * self.alpha0 + self.sample_size)
        return np.sum(gausses, axis=-1)

    def classify(self, X):
        return np.argmax(self.e_like_step(X), 1)

    def student_t(self, X):
        nu = self.nu + 1 - self.ndim
        L = nu * self.beta * self.W / (1 + self.beta)
        d = X[:, :, None] - self.m
        maha_sq = np.sum(np.einsum('nik,ijk->njk', d, L) * d, axis=1)
        return (
            gamma(0.5 * (nu + self.ndim))
            * np.sqrt(np.linalg.det(L.T))
            * (1 + maha_sq / nu) ** (-0.5 * (nu + self.ndim))
            / (gamma(0.5 * nu) * (nu * np.pi) ** (0.5 * self.ndim)))

    def predict_dist(self, X):
        return (self.alpha * self.student_t(X)).sum(axis=-1) / self.alpha.sum()


def create_toy_data():
    x1 = np.random.normal(size=(100, 2))
    x1 += np.array([-5, -5])
    x2 = np.random.normal(size=(100, 2))
    x2 += np.array([5, -5])
    x3 = np.random.normal(size=(100, 2))
    x3 += np.array([0, 5])
    return np.vstack((x1, x2, x3))


def main():
    X = create_toy_data()

    model = VariationalGaussianMixture(n_component=10, alpha0=0.01)
    model.fit(X, iter_max=100)
    labels = model.classify(X)

    x_test, y_test = np.meshgrid(
        np.linspace(-10, 10, 100), np.linspace(-10, 10, 100))
    X_test = np.array([x_test, y_test]).reshape(2, -1).transpose()
    probs = model.predict_dist(X_test)
    plt.scatter(X[:, 0], X[:, 1], c=labels, cmap=cm.get_cmap())
    plt.contour(x_test, y_test, probs.reshape(100, 100))
    plt.xlim(-10, 10)
    plt.ylim(-10, 10)
    plt.show()


if __name__ == '__main__':
    main()

結果

下の動画は変分ベイズ法を用いてクラスタリングを行っている様子を表しています。点の色がどのクラスタに属しているのかを表していて、学習が進むにつれて有効な混合要素数が減り、最終的に3つとなっています。（上記のコードはこのような途中経過は表示せずに最終結果だけ図示します）

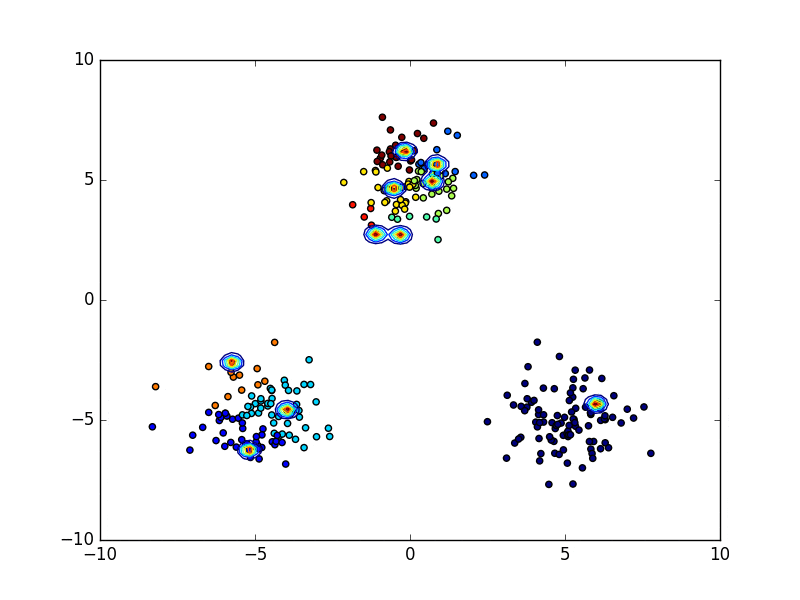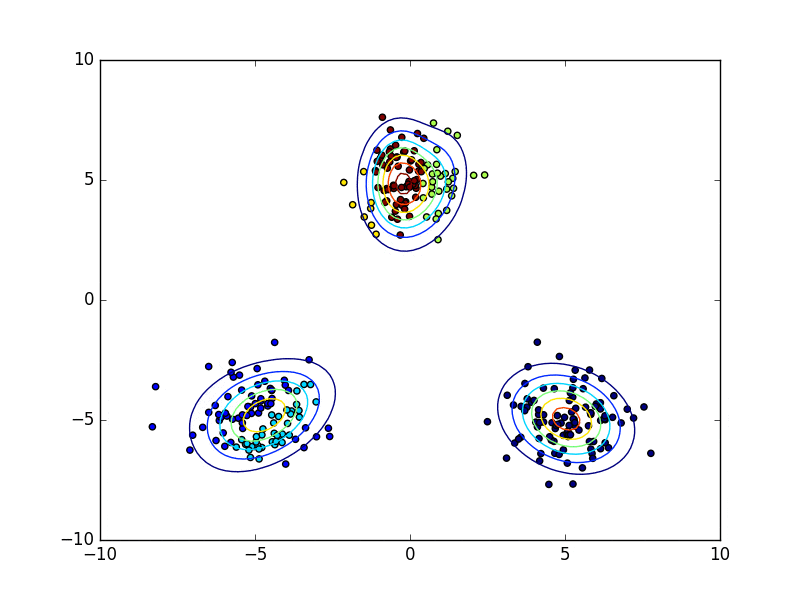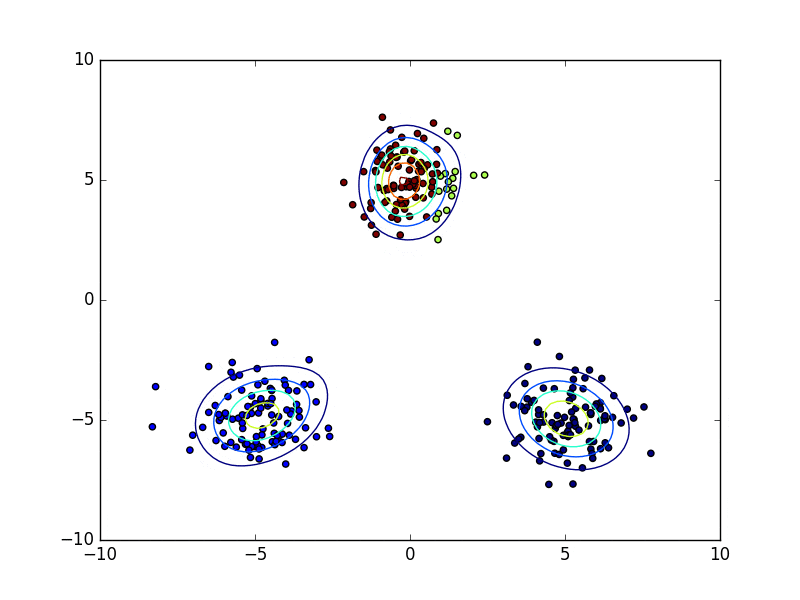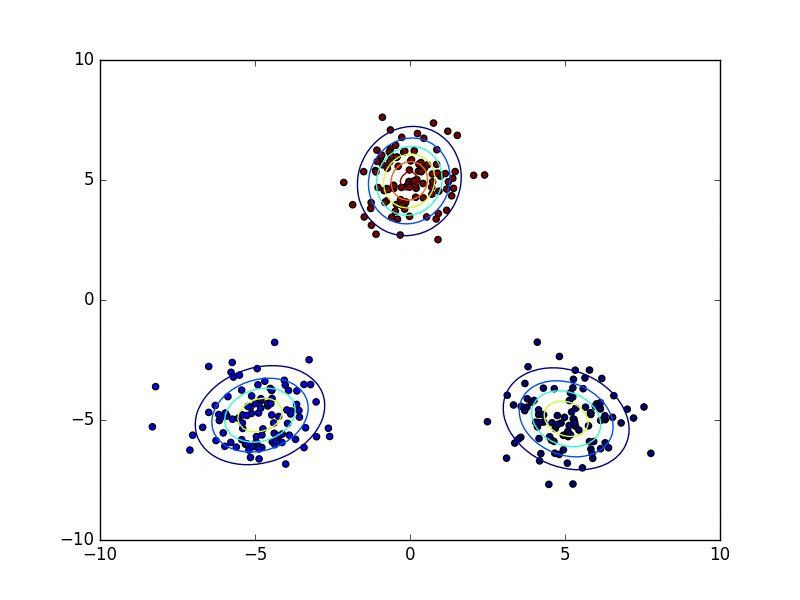
終わりに

PRMLの第10章では混合ガウスだけでなく線形回帰、ロジスティック回帰に変分ベイズ法を使っている例が紹介されているので、それらも機会があれば実装していきます。