この記事は 本郷学園マイコン部 Advent Calendar 2024 9日目の記事です。
tl;dr
Wolframの基本セルオートマトンをHSPで実装しました。たのしかったです。
背景
図書館運営委員会の先生に「情報系のいい本があったら所蔵リクエストを出してくれ」という素晴らしいオファーを頂いたので、図に乗ってこんなものまで頼んでしまいました:
というわけで、責任を取ってこれについて一筆書くことにしました。
基本セルオートマトンとは?
Stephen Wolframはコンピュータを用いて「シンプルなプログラム」の実験を行う中で、彼の新しい科学のアイデアを得たそうです。中でも基本セルオートマトンは最初期に彼へ洞察を与えた「シンプルなプログラム」として、NKSの中でも大変多くのページを割いてそのふるまいが詳細に調べ上げられています。
基本セルオートマトンは、3近傍・2状態の1次元セルオートマトンです。無数のセルが横一列に並んでおり、これらは常に0または1のいずれかの状態を取っています。各セルは自身と両隣が現在取っている状態のみに基づいて次に取る状態を定めます。
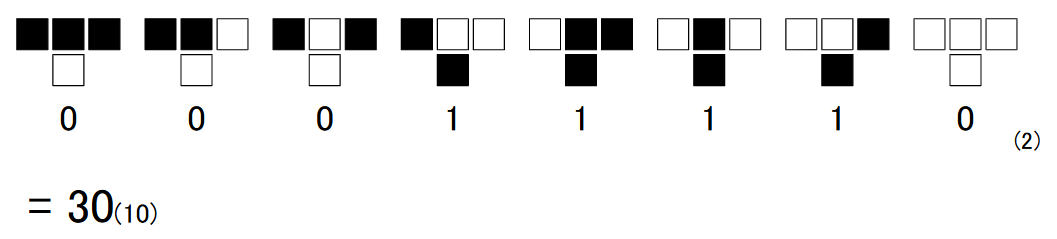
例として、ルール30の状態遷移表を下に示します。セル3つ組の状態によって定まる遷移後の状態の列を8桁の2進数として見ると、このルールを表す自然数30が得られます。
状態0で初期化されたセル列の中央に一つだけ状態1のセルを置き、この状態遷移ルールを繰り返し適用すると、下に示す非常に乱雑なパターンが現れます。
空間は1次元、時間も空間も状態も離散的、各セルは現在の両隣しか参照できないなどという迫害的に厳しい規則からでもこのような複雑な振る舞いが生まれるのは大変感動的で、Wolframがここから新しい種類の科学について洞察を得たというのもうなずけます。
HSPによる実装
カレントウィンドウ全面に基本セルオートマトンのパターンを表示する命令caを定義したヘッダファイルca.asおよび、この命令を使用するプログラムmain.hspを記述しました。
#include "ca.as"
ca 30, 1, 0, 0
// cell_automaton/ca.as
// by ctes091x (2022)
#module
#deffunc ca int rule_code, int cell_size, int is_rand, int boundary_condition
randomize
/*ルールの生成
2のcnt乗桁目のビットが1なら配列の対応する箇所に1を代入
ルールを表す自然数をビットごとに切り出して配列にする*/
dim rule, 8
repeat 8
if rule_code and int(powf(2,cnt)) : rule(cnt) = 1
loop
//状態遷移と表示
size = ginfo_winx / cell_size
height = ginfo_winy / cell_size
dim cells, size
//真ん中に1を置く
cells(int(size/2)) = 1
//ランダム化
if is_rand {
repeat size
cells(cnt) = rnd(2)
loop
}
dim tmp, size
//現在の表示座標
x = 0 : y = 0
repeat height
redraw 0
x = 0
//端点の処理
switch boundary_condition
case 0
//周期的境界条件
cells(0) = cells(size-2)
cells(size-1) = cells(1)
swbreak
case 1
//固定的境界条件(0)
cells(0) = 0
cells(size - 1) = 0
swbreak
case 2
//固定的境界条件(1)
cells(0) = 1
cells(size - 1) = 1
swbreak
case 3
//反射的境界条件
cells(0) = cells(1)
cells(size - 1) = cells(size - 2)
swbreak
case 4
//散逸的境界条件
cells(0) = rnd(2)
cells(1) = rnd(2)
swbreak
swend
repeat size - 2, 1
//出力
if cells(cnt) == 0 {
color 255, 255, 255
} else : if cells(cnt) == 1 {
color 0, 0, 0
}
boxf x * cell_size, y * cell_size, x * cell_size + cell_size, y * cell_size + cell_size
// 近傍の状態を3桁の2進数->10進数に変換、ルールから対応する0または1を取得し次に取る状態に代入
tmp(cnt) = rule((cells(cnt - 1) * 4) + (cells(cnt) * 2) + (cells(cnt+1) * 1))
x += 1
loop
// 次に取る状態を`cells`に代入
repeat size - 2, 1
cells(cnt) = tmp(cnt)
loop
//y座標に1を足す
y += 1
redraw 1
await 1
loop
return
#global
結果
記述したプログラムを実行すると、カレントウィンドウ上にルール30の状態遷移履歴が表示されます。
画面の左右両端のセルにはそれぞれ左/右隣のセルを持ちませんが、今回のプログラムではこの両端を繋ぎ空間を円環状にすることで、全セルの状態遷移を計算できるようにしています。
命令caには第一パラメータとしてルールの番号を与えており、異なるルールに従う基本セルオートマトンも表示できます。
ルール90はシェルピンスキーのガスケットというフラクタル図形を生成します。
ルール110は、局所的なパターンが相互作用する非常に複雑なパターンを生成します。このセルオートマトンはチューリング完全であり、これを示す論文は2004年にComplex System誌に掲載されました。
感想
NKSを読み進めるのが楽しみです。
明日も私のHSPで3状態総和型セルオートマトンを書いて遊ぶ【NKS】です。
参考文献
- S. Wolfram, A New Kind of Science. Wolfram Media, 2002.
フルテキストがオンラインで参照可能。学校図書館に買ってもらう必要あったのか...? - M. Cook, “Universality in Elementary Cellular Automata,” Complex Systems, vol. 15, no. 1, pp. 1–40, Mar. 2004, doi: https://doi.org/10.25088/complexsystems.15.1.1.
- グレッグ・イーガン, 山岸真訳, 『順列都市 上・下』ハヤカワ文庫SF, 1999.
人間の精神をソフトウェア化する〈コピー〉が一般的となりつつある近未来。模擬化学セルオートマトン「オートヴァース」に傾倒するマリアは、富豪たちに「不死」を売り込んでいるという男ポールに奇妙な依頼を受ける。例外ルールの集合体である〈コピー〉とは異なり、空間全体が均一なルールで進行するオートヴァースのエレガントさをマリアが恋人に語るシーンには一見の価値がある。(隙あらば布教)(本記事では微塵も参照していない)