1次元波動方程式の数値計算
波動方程式とは
波動方程式とは以下のような形をした、時間に関する2階微分と、空間に関する2階微分を含んだ偏微分方程式です。
\frac{\partial^2 u}{\partial t^2} = c^2 \frac{\partial^2 u}{\partial x^2}
この方程式によって、波が空間を伝わる様子をあらわすことができます。つまり波動砲です。
時間と空間の離散化
元の方程式は連続な時間 $[0, T]$ と空間 $[0, X]$ の上で定義されているとします。数値計算をするためには、これを離散化する必要があります。時間も空間も一定の区間の中には「無限」に点があるのですが、これら全てについて計算することはできないためです。
そこで、飛び飛びの時間 $t_0 = 0 < t_1 < \dots < t_i < \dots < t_N = T$ および飛び飛びの空間の点 $0 < x_1 < \dots < x_j < \dots < x_M < X$ を選び、微分方程式の解がその時間とその空間の点でどんな値をとるのか、すなわち $ u(t_i, x_j) $ を近似的に求めていきます。
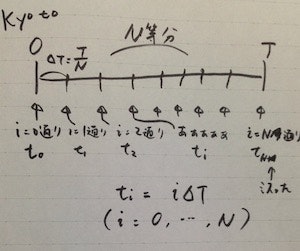
実は既に答えを書いているのですが、時間については以下のように離散化します。
区間 $[0, T]$ を $N$ 等分すると、 $N+1$ 個の点がとれます。これを添字として $i = 0, \dots, N$ (全部で $N+1$ 個)を使って区別します。点と点との間は $\Delta T = T/N$ 離れています。飛び飛びの時間 $t_i$ をその点にとります。 つまり
t_i = i \Delta T
となります。
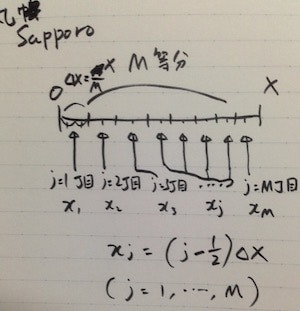
空間については以下のように離散化します。
区間 $[0, X]$ を $M$ 等分すると、$M$ 個の区間がとれます。これを添字として $j = 1, \dots, M$ (全部で $M$ 個)を使って区別します。区間の長さは全て $\Delta X = X/M$ です。飛び飛びの空間 $x_j$ を区間の真ん中の点に取ります。つまり
x_j = \left( j - \frac{1}{2} \right) \Delta X
となります。
似ているようで微妙に異なりますね。ここで利用した時間の離散化方式を「京都方式」、空間の離散化方法を「札幌方式」と(ごく一部のマニアの間で)呼んでいます。
京都市では「通り」にラベルがつけられており、京都市の住所は、基本的に東西・南北2つのラベルの組み合わせ(格子点)が住所を特定する単位です。あとはそこから東に入ったり西に入ったり上がったり下がったりするだけです。知らんけど。
一方札幌では、南北はやはり通りにラベルがついていますが、東西は2つの通りにはさまれた「ブロック」の方にラベルがつけられており、それが住所を特定する単位です。たとえば北N条東M丁目という住所において、北N条は通りの名前ですが、東M丁目はブロックの名前です。
方程式の差分化
波動方程式を数値計算するための第一歩として、中心差分法という方法を使います。ある関数 $f$ の点 $x$ における の微分 $f'(x)$ を、その「両隣」の点 $x + \Delta x$, $x - \Delta x$ を加えて、元の関数の3つの点での値 $f(x)$, $f(x+\Delta x)$, $f(x-\Delta x)$ から近似的に計算する方法です。
まず、 $f$ を $x + \Delta x$, $x - \Delta x$ でそれぞれテイラー展開してしまいます。
f(x+\Delta x) = f(x) + \frac{f'(x)}{1!} \Delta x + \frac{f''(x)}{2!} \Delta x^2 + \frac{f''(x)}{3!} \Delta x^3 + (\Delta x の 4次以降の項) \\
f(x-\Delta x) = f(x) - \frac{f'(x)}{1!} \Delta x + \frac{f''(x)}{2!} \Delta x^2 - \frac{f''(x)}{3!} \Delta x^3 + (\Delta x の 4次以降の項)
そして、これらを足し合わせます。
f(x+\Delta x) + f(x-\Delta x) = 2f(x) + f''(x) \Delta x^2 + (\Delta x の 4次以降の項)
さらに変形するとこうなります。
f''(x) = \frac{f(x+\Delta x) - 2f(x) + f(x-\Delta x)}{\Delta x^2} + (\Delta x の 2次以降の項)
$\Delta x$は元々小さめに取るので、$\Delta x$の2次以降の項はもっと小さくなります。いっそ $0$ と思ってしまいましょう。たとえば $\Delta x = 0.01$ なら $\Delta x^2 = 0.0001$ です。すると最後にはこうなります。
f''(x) = \frac{f(x+\Delta x) - 2f(x) + f(x-\Delta x)}{\Delta x^2}
こうして2階微分を、両隣の点を使ってはいるものの元の関数だけであらわせたのでした。これを波動方程式に使うとこうなります。
\frac{u(t+\Delta t, x) - 2u(t, x) + u(t-\Delta t, x) }{\Delta t^2} = c^2 \frac{u(t, x+\Delta x) - 2u(t, x) + u(t, x-\Delta x) }{\Delta x^2}
$\lambda = c \frac{\Delta t}{\Delta x}$とおいて、がんがん変形します。
u(t+\Delta t, x) = 2(1-\lambda^2) u(t, x)+\lambda^2 u(t, x+\Delta x) + \lambda^2 u(t, x-\Delta x) - u(t-\Delta t, x)
初期条件の処理
先ほどの式の右辺をながめてみると、最初の3項は時刻 $t$ における $u$ の情報であり、最後の項だけ時刻 $t-\Delta t$ で「一つ前」の時刻の情報です。左辺は未来の時刻 $t+\Delta t$ の情報なので、この式を計算し続けることで、過去から未来に向かって $u(t, x)$ を計算し続けることができます。また、計算の手順を逆にたどると分かりますが、「最初」の状態 $u(0, x)$ だけは全ての $x$ について値を決めなければいけません。これを初期値あるいは初期条件と呼びます。ただし、必要な初期条件は後もう一つあります。
時間と空間はすでに以前の章で離散化していたのでした。これを用いると以下のように書き直せます。
u(t_{i+1}, x_j) = 2(1-\lambda^2) u(t_i, x_j)+\lambda^2 u(t_i, x_{j+1}) + \lambda^2 u(t_i, x_{j-1}) - u(t_{i-1}, x_j)
ここで $i = 0, ..., N$, $j = 1, \dots, M$ となります。 $i = 0$ のときの $u(t_0=0, x_j)$ は初期値として、こちらが決めてしまいます。また $i = 0$ のときは
u(t_1, x_j) = 2(1-\lambda^2) u(0, x_j)+\lambda^2 u(0, x_{j+1}) + \lambda^2 u(0, x_{j-1}) - u(t_{-1}, x_j)
となってしまうのですが、 $u(t_{-1}, x_j)$ もまた初期条件として与える必要があります。これは「初速」 $\frac{\partial u}{\partial t}(0, x)$ を決めることで求めることができます。
微分を差分化するためにもう一度テイラー展開をしましょう。ただし今度は3次以降の項をまとめます。
f(x+\Delta x) = f(x) + \frac{f'(x)}{1!} \Delta x + \frac{f''(x)}{2!} \Delta x^2 + (\Delta x の 3次以降の項) \\
f(x-\Delta x) = f(x) - \frac{f'(x)}{1!} \Delta x + \frac{f''(x)}{2!} \Delta x^2 + (\Delta x の 3次以降の項)
今度はこれらを引き算します。変形すると以下のようになります。
f'(x) = \frac{f(x+\Delta x) - f(x-\Delta x)}{\Delta x} + (\Delta x の 2次以降の項)
$\Delta x$の2次以降の項はやはり誤差の範囲と思いましょう。 $u(t, x)$ に話を戻すと
\frac{\partial u}{\partial t}(0, x) = \frac{u(t_1, x) - u(t_{-1}, x)}{\Delta T}
これを変形すると
u(t_{-1}, x) = u(t_1, x) - \frac{\partial u}{\partial t}(0, x) \Delta T
これを $u(t_1, x) = \cdots$ の式に戻して変形すると以下のようになります。
u(t_1, x_j) = (1-\lambda^2) u(0, x_j)+\frac{\lambda^2}{2} u(0, x_{j+1}) + \frac{\lambda^2}{2} u(0, x_{j-1}) + \frac{1}{2} \frac{\partial u}{\partial t}(0, x_j) \Delta T
境界条件の処理
問題はまだあります。空間の「左端」 $j = 1$ における点 $x_1$ にはもうその左隣 $x_{j-1}$ がありません。同様に、空間の「右端」 $j=M$ においてもその右隣はありません。
ここでも数学的あるいは物理的に「もっともらしい」条件を設定してなんとかしてやる必要があります。これを境界条件と呼んでいます。境界条件には色々なパターンがあるのですが、今回は「区間の端で微分が0」という条件(端がちゅうぶらりんになっている状態)を課します。先に示した札幌方式による空間の離散化
x_j = \left( j - \frac{1}{2} \right) \Delta X
において、便宜的に $j = 0$ の点 $x_0$ を考えると、これは元の区間 $[0, X]$には入っていませんが、 $x_0$ と $x_1$ のちょうど中間が $x = 0$ (区間の左端)になっています。ここで微分が0となるので、境界条件は
u(t_i, x_0) = u(t_i, x_1)
となります。区間の右端でも同様に、$j = M+1$ の点 $x_{M+1}$ を考えると
u(t_i, x_{M+1}) = u(t_i, x_M)
となります。これで空間の端でも $t_{i+1}$ の値が計算できます。
行列を用いた表現
これまでの話をまとめると、波動方程式を数値計算するためには以下の式を計算すればよかったのでした。
u(t_{i+1}, x_j) = 2(1-\lambda^2) u(t_i, x_j)+\lambda^2 u(t_i, x_{j+1}) + \lambda^2 u(t_i, x_{j-1}) - u(t_{i-1}, x_j)
$j$ は基本的に $j = 1, \dots, M$ なのですが、両端に限り $u(t_i, x_0) = u(t_i, x_1), u(t_i, x_{M+1}) = u(t_i, x_M)$ として計算をします。$u(t_i, x_j)$ を計算するためには、これらの式をなんども繰り返し計算しなければいけません。
たとえばC言語であれば「iに関するforループ」と「jに関するforループ」をぐるぐるする必要があるでしょう。
やりたくないですよね。
やらなくていいんです。
Pythonですから。
そのためには、以下のように行列を利用した表現に書き直してやる必要があります。
\begin{pmatrix}
u(t_{i+1}, x_0)\\
u(t_{i+1}, x_1)\\
u(t_{i+1}, x_2)\\
\vdots\\
u(t_{i+1}, x_{M-1})\\
u(t_{i+1}, x_M)\\
u(t_{i+1}, x_{M+1})\\
\end{pmatrix} =
\begin{pmatrix}
\lambda^2 & 2(1-\lambda^2) & \lambda^2 & & & & &\\
\lambda^2 & 2(1-\lambda^2) & \lambda^2 & & & & &\\
& \lambda^2 & 2(1-\lambda^2) & \lambda^2 & & & &\\
& & \ddots & \ddots & \ddots & & &\\
& & & \lambda^2 & 2(1-\lambda^2) & \lambda^2 & &\\
& & & & \lambda^2 & 2(1-\lambda^2) & \lambda^2 &\\
& & & & \lambda^2 & 2(1-\lambda^2) & \lambda^2 &\\
\end{pmatrix}
\begin{pmatrix}
u(t_i, x_0)\\
u(t_i, x_1)\\
u(t_i, x_2)\\
\vdots\\
u(t_i, x_{M-1})\\
u(t_i, x_M)\\
u(t_i, x_{M+1})\\
\end{pmatrix} -
\begin{pmatrix}
u(t_{i-1}, x_0)\\
u(t_{i-1}, x_1)\\
u(t_{i-1}, x_2)\\
\vdots\\
u(t_{i-1}, x_{M-1})\\
u(t_{i-1}, x_M)\\
u(t_{i-1}, x_{M+1})\\
\end{pmatrix}
空欄は0です。$j = 0, M+1$ のところは境界条件を満足するように「調整」した結果です。行列は「定数行列」なので与えられたパラメータを利用して初めから計算可能です。また $i = 0$ の場合は多少異なる式になりますが、元の式はすでに計算してあるので、対応する行列は各自で求めてください。
これでようやくPythonで数値計算できるかたちになりました。ただの行列およびベクトルの計算まで落とし込むことができた上に、行列は疎(スパース)なのでnumpyが縦横無尽に活躍しそうですね。GPUを用いた計算も簡単にできそうです。
くたばれC言語!!
さてお待ちかね、Pythonのコードです↓↓↓↓
Pythonコード
なんとここでタイムアップ!
書ききれませんでした〜
気が向いたら追記します :dogeza:
おわりに
Pythonを使って波動方程式を数値的に解いてみましたくことができませんでした。
いかがでしたか?
おわびに
すいませんでした。
マイクロアドでもこのような数値計算を日々行なって**いません。**データサイエンティストという人たちがいまして、機械学習で色々やっています。データサイエンティストの採用も積極的に行なっているようです。なお私はデータサイエンティストではありません。
また今回時間を離散化するために利用した方法を「京都方式」と呼びましたが、そういえばマイクロアドも京都に拠点があります。人数は少ないですが、スキルの高い精鋭エンジニア集団です。なお私は京都では勤務していません。
ではまた〜