金融予測ラベリング応用編： コールオプション戦略

イントロダクション

どうも、KOです。最近のマイブームがボラティリティで、ボラティリティが一番活用できる金融商品って先物オプションだと思うんですよね。
なので、今回はコールオプションによるラベル付けを行いたいと思います。ついでに、ブラックショールズモデルからヒストリカルのオプションの価格の乖離も見ていきたいと思います。

コールオプションのペイオフ

ここでのコールオプションはヨーロピアンオプションとします。
現在時刻と$t=0$,満期を$t=T$とします。コールオプションの価値を$C(S_t, t)$とします。コールオプションの満期における価値は定義より以下の通りです。
$$C(S_T, T) = (S_T-K, 0)^{+}$$
ただし、$S_t$は時刻$t$の株価、$K$は権利行使価格とします。
時刻$t$におけるブラックショールズモデルによるコールオプションの価値は
$$C(S_t, t) = S_t N(d_1) - K e^{-r(T-t)}N(d_2)$$
ただし、
$$\displaystyle N(x) = \frac{1}{\sqrt{2\pi}}\int_{-\infty}^{x}e^{\frac{-y^2}{2}}dy$$
$$d_1 = \frac{\log{\frac{S_t}{K}}+(r+\frac{\sigma^2}{2})(T-t)}{\sigma \sqrt{T-t}}$$
$$d_1 = \frac{\log{\frac{S_t}{K}}+(r-\frac{\sigma^2}{2})(T-t)}{\sigma \sqrt{T-t}}$$

データセット

今回は皆さんもお馴染みの日経平均株価の終値を使用したいと思います。1949年から2020年のデータを用います。現在との価格差があまりにも大きすぎるので、絶対差分ではなく$S_t$との変化率を見ます。

	close
DATE
1949-05-16	176.210007
1949-05-17	174.800003
1949-05-18	172.529999
1949-05-19	171.339996
1949-05-20	169.199997
1949-05-23	171.850006
1949-05-24	172.750000
1949-05-25	171.529999
1949-05-26	170.429993
1949-05-27	172.759995

ATMのコールオプションのラベリング

ATMはAt the moneyで現在価格と同じと意味します。銀行のATMとは特に関係はありません。そのほかの用語に、ITM(In the money)、OTM(Out of the money)もあります。

T = 20 #残存期間
labels["price diff"] = labels["close"].shift(-T)/labels["close"]-1
labels["ATM"] = 0
labels["bin"] = labels[["price diff", "ATM"]].max(axis=1)
labels = labels[["bin"]]
labels

分析

ATMのコールオプションが実際に権利を行使出来た確率が57.9%になります。戦後からずっと価格が上がり続けているので、こういった偏った結果になっているのでしょう。
また、歴史的には平均利益(0を含む)は2.5507%になっております。つまり、現在の日経平均株価が20000円だとするなら、20000円のコールオプションはヒストリカル平均は510円ってことになります。

理論値

from scipy.stats import norm

def get_BS_call(S0, sigma ,r,q,T,K):
    '''
    S0    : 現在価格
    sigma : ボラティリティ
    r     : 金利
    q     : 配当
    T     : 残存期間
    K     : 権利行使価格
    '''
    d1 = (np.log(S0 / K) + (r - q ) * T) / (sigma * np.sqrt(T))+sigma*np.sqrt(T)/ 2
    d2 = (np.log(S0 / K) + (r - q ) * T) / (sigma * np.sqrt(T))-sigma*np.sqrt(T)/ 2

    return S0 * np.exp(-q * T)* norm.cdf(x=d1, loc=0, scale=1) -K * np.exp(-r * T) * norm.cdf(x=d2, loc=0, scale=1)

では、理論価格出していきましょう。

sample_df = df.copy()
sample_df["HV"] = np.log(sample_df["close"]).diff().rolling(T).std()
sample_df["r"] = 0
sample_df["q"] = 0
sample_df["T"] = T
sample_df["K"] = sample_df["close"]
sample_df.dropna(inplace=True)
sample_df.head()

#コールオプションを計算する。
sample_df["BS_Call"] = BS_Call(sample_df["close"], sample_df["HV"], sample_df["r"], sample_df["q"], sample_df["T"], sample_df["K"])
sample_df.head()

	close	HV	r	q	T	K	BS_Call
DATE
1949-06-15	153.809998	0.014752	0	0	20	153.809998	4.047386
1949-06-16	157.800003	0.016427	0	0	20	157.800003	4.623628
1949-06-17	160.130005	0.016884	0	0	20	160.130005	4.822376
1949-06-20	155.449997	0.017848	0	0	20	155.449997	4.948716
1949-06-21	152.990005	0.017941	0	0	20	152.990005	4.895667

これによると、5月8日時点での残存期間20日の20179円のコールオプションは678円ですね。ただ、実際のマーケットは権利行使価格が125円刻みであったり、マーケット価格も離散的なので、実務で応用する場合にはもう少し工夫する必要はある。

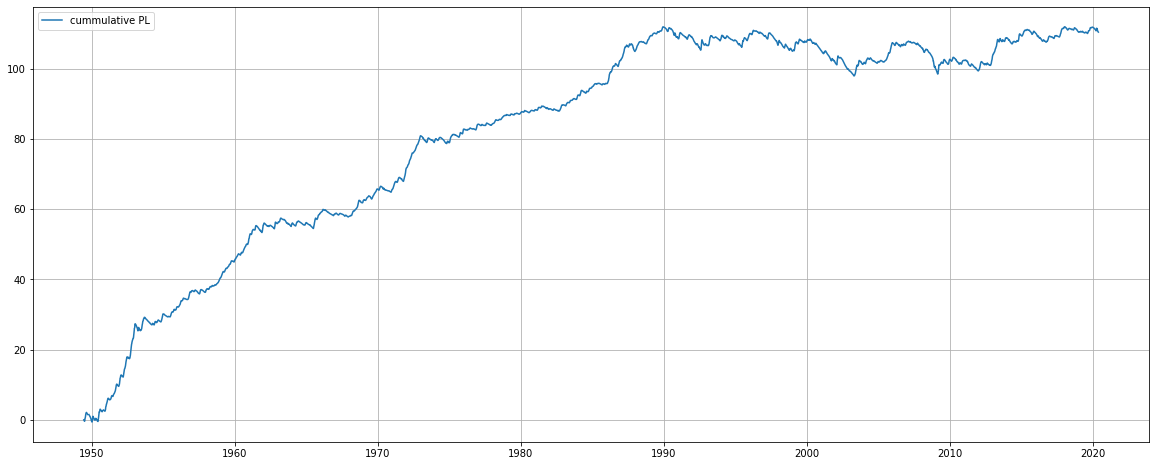
ATMのコールオプションを買い続けていたら？

本来のマーケット価格はヒストリカルボラティリティを用いておらず、かなりズレます。しかし、マーケットデータを持っていないので、これを理論価格だとして計算してみます。

今回の計算は%なので、最初の資産が1だと仮定しても単利でも100倍以上になっていた計算になります。
仮にマーケットで理論価格よりも安く購入できるのであれば、もっと有利になります。逆に高く購入することになると不利になるので、ちゃんと価格と理論価格を見て投資判断したほうが良いでしょう。

結論

オプションは男の浪漫です（笑）