【ICLR論文紹介】Generating High Fidelity Images with Subscale Pixel Networks and Multidimensional Upscaling

ICLR2019を読むQiitaのアドベントカレンダーに参加してみました。
アドベントカレンダー本体のリンクは以下です。
ICLR2019をよむアドベントカレンダー Advent Calendar 2018

Generating High Fidelity Images with Subscale Pixel Networks and Multidimensional Upscaling
今回取り上げる論文はこちらです。
double-blind reviewなのでどこの誰かと思っていたらDeepMindでした（そもそも学習にTPU podが使われていた時点で）。

openreviewのリンクはこちら。

様々なドメインで成功を収めている深層生成モデルについて、条件なしの高解像度の画像生成が未だ困難であることを挙げ、自己回帰モデルをベースに"Subscale Pixel Network（SPN）"と"Multidimensional Upscaling"という2つの工夫を提案し、画像生成の尤度で最先端の結果（state-of-the-art, SOTA）を達成しています。

概略

生成モデルとして現在有力な方針の1つに自己回帰モデル（Autoregressive Model, AR Model）があります。これは以下のような式で表現されます。

p({\bf x}) = \prod_{t=1}^{T}P(x_t|x_1, ..., x_{t-1})

これは、生成対象の確率や尤度をより分かりやすい形でモデル化するため、変数の次元同士の依存関係を1方向のみに制限し、「それまでに生成された次元の変数で条件付けられた各次元の変数の確率の積」という形で因数分解していることに相当します。

画像生成の場合、これは以下のような式で表現されます（論文中の式(1)に対応しています）。

p({\bf x}) = \prod_{h=1}^{H}\prod_{w=1}^{W}\prod_{c}^{\{R,G,B\}}P(x_{h,w,c}|{\bf x}_{<})

ただし、h, w, cはそれぞれ画像の行、列、チャネルに対応しており、${\bf x_<}$は$x_{h,w,c}$よりも前に生成された全ての変数を表しています。これは、以下の図のようにラスタスキャン的に左上から順に画像を生成していることに相当します。

このようにして左上から順に画像を生成すると、画像の左上と右下のように遠く離れた領域で依存関係があるような構造を生成することは難しくなります。
よって、画像生成への自己回帰モデルの単純な適用では高解像度の画像を意味的な一貫性を維持しつつ生成することは難しいといえます。
本論文では、以下で説明する"subscale ordering"に従ってアップスケーリングしつつ画像生成を行うSubscale Pixel Network（SPN）でこの問題点に取り組んでいます。

また、高解像度の画像の生成におけるもう1つの困難な点として、バリデーションデータに対する尤度の向上と生成画像のクオリティの向上は単純に対応していないことが挙げられます。
尤度最大化による学習は、人間から見た画像のクオリティにそこまで影響しない部分も含めた経験分布全体をモデルに再現させようとしてしまう傾向があります。

GAN¹などは直接的に尤度を最大化せずに識別器（Discriminator）を介して訓練画像の情報を伝達することで、この問題を上手く回避していると言えます。
本論文では、以下で説明する"depth upscaling"によって、画素の値に関してより重要なビット（上位ビット）にまず着目させることでこの問題点に取り組んでいます。

subscale ordering

論文中のFigure 3を以下に示します。

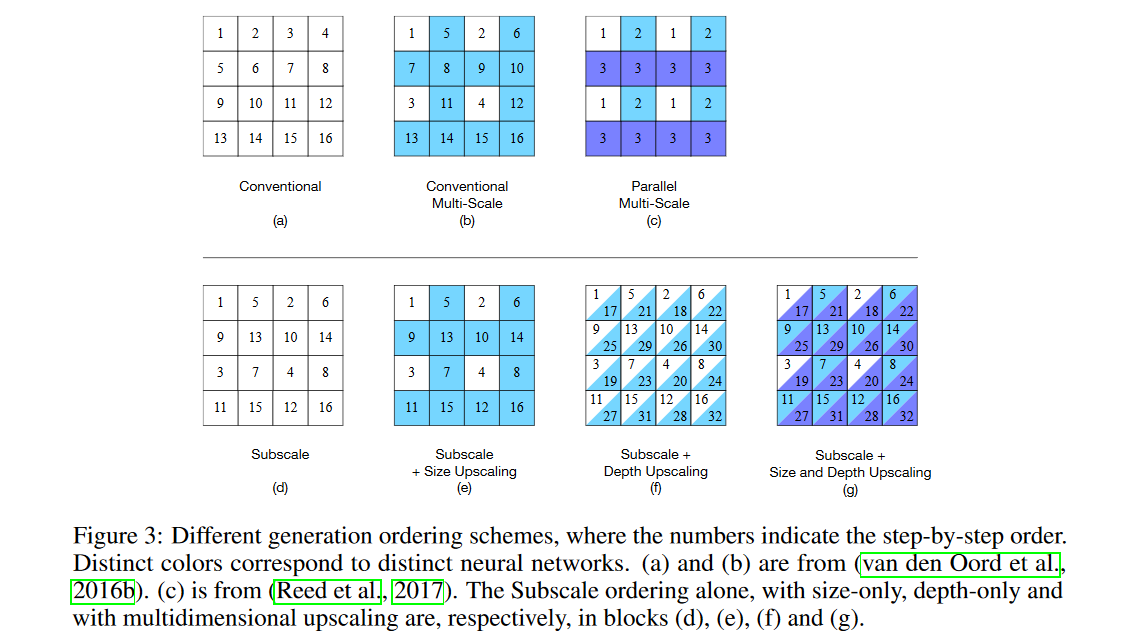
上図中の(a)が通常の自己回帰モデルによる生成順序を表しています。subscale orderingでは、生成の順序を上図中の(d)の生成順序に変更します。
これを分かりやすさの為に別の色で塗り分けると、以下の図のようになります。

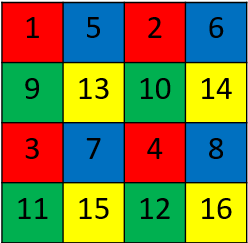
これは、画像全体を赤、青、緑、黄色のそれぞれ元の画像の1/4のサイズの画像4つに分割し、それぞれの分割された画像（以下スライス）内での生成は自己回帰モデルで行い、赤→青→緑→黄色の順番で各スライスを生成し、最後にまとめていると解釈できます。

数式で表すと以下のようになります（論文中の式(2)に対応しています）。

p({\bf x}) = \prod_{i=1}^{S}\prod_{j=1}^{S}\prod_{h=1}^{H/S}\prod_{w=1}^{W/S}\prod_{c}^{\{R,G,B\}}P(x_{i+S*h, j+S*w,c}|{\bf x}_{<})

ここで、先程の式から新たに出現した$S$という文字は、元の画像を縦、横方向に幾つのスライスに分割するかのスケーリングファクターを表しています。
縦と横方向それぞれで$S$個のスライスに分割するため、最終的には$S^2$個のスライスに分割することになります。先程の例は$S=2$の場合に相当します。
スライスの中では自己回帰モデルによって左上から順にラスタスキャン的に画像を生成し、かつ各スライスはそれまでに生成された全てのスライスにも条件付けられています。

このように自己回帰モデルの生成順序を工夫することによって、高解像度の画像を生成するにあたっても比較的広範囲の依存関係をモデル化しやすくしています。
また、各スライスの画像生成を行う自己回帰モデルは重みを共有することで、パラメータを削減することにも成功しています。

このsubscale orderingを採用した自己回帰モデルの重要な点として、生成したい画像サイズに対して$1/S^2$のサイズのスライスを最初に生成し、それによって条件付けて他のスライスを生成することで最終的に目的のサイズの画像を生成するため、暗黙的にアップスケーリングを行っていると解釈することが出来ます。

ここで、最初に$1/S^2$のサイズのスライスを生成する代わりに、外部から初期値として画像を与えることによって、明示的にアップスケーリングを行うことができ、これによって以下に示すFigure 1でのSize Upscalingを実行しています。

先程の4色で塗り分けた画像の例で言えば、赤で塗られた部分のスライスを生成する代わりにそこに外部からの画像を配置し、他の処理は同様に実行することで画像のアップスケーリングを実行できるということです。

depth upscaling

論文中のFigure 1を以下に示します。

depth upscalingの操作は数式上では分かりにくいため最初に視覚的に示してしまうと、上図のFigure 1の左端及び右端で行っている操作のことです。
色合いに乏しい画像から、複雑な色合いの画像に変化していることが分かります。
この各ピクセルの各色の強度を表すビット方向の次元をdepth方向と呼びます。

以下に数式上の表記を示します。
depth方向に画像を最初の$d_1$ビット、次の$d_2$ビットと分割した場合、生成の第1ステージは以下のようになります（論文中の式(3)に対応しています）。
分かりやすさのため、subscale orderingの記法ではなく通常の画像生成における自己回帰モデルの記法を用いています。

p({\bf x}^{:{\bf d_1}}) = \prod_{h=1}^H\prod_{w=1}^W\prod_c^{\{R,G,B\}}P({\bf x_{h,w,c}}^{:{\bf d_1}}|{\bf x}^{:{\bf d_1}}<)

ここで、自己回帰モデルによってまず最初の$d_1$ビットを生成しています。

次に、生成の第2ステージは以下のようになります（論文中の式(4)に対応しています）。

p({\bf x}^{:{\bf d_1}}) = \prod_{h=1}^H\prod_{w=1}^W\prod_c^{\{R,G,B\}}P({\bf x_{h,w,c}}^{{\bf d_1}:{\bf d_2}}|{\bf x}^{{\bf d_1}:{\bf d_2}}<, {\bf x}^{:{\bf d_1}})

ここで、最初に生成された$d_1$ビットの画像で全体を条件づけながら、自己回帰モデルによって残りの$d_2$ビットまでを生成しています。

depth方向により細かく分割した場合は、この処理を繰り返します。

この操作の目的は、最初に上位ビットをより顕著で重要なビットとして生成し、その後それによって条件づけて下位ビットを生成することで、重要度の低い下位ビットの値によって重要度の高い上位ビットの値の予測が影響を受けることを防ぎ、より外見上高精細な画像を生成することです。

Multidimensional Upscaling with SPN

最終的な全体のパイプラインとしては、上のFigure 1の右側に示されているように、初めに小さな画像を生成し、それをsubscale orderingを用いたSubscale Pixel Network（SPN）に与えることで明示的にサイズのアップサンプリングを行います。

ここまでの処理はいずれも上位ビットに対してのみ行い、最後にdepth upscalingで上位ビットの画像で条件づけながら下位ビットの生成も行うことで画像生成を完了します。

前述したように、depth upscalingの説明で示した式は説明をシンプルにするためにsubscale orderingの記法を使わずに書かれていますが、実際にはここでもsubscale orderingを用いています（上のFigure 3の(f)や(g)を参照してください）。

以上のようにサイズ方向とdepth方向の両方に対してアップスケーリングを行うため、Multidimensional Upscalingと呼ばれます。

Subscale Pixel Network（SPN）は、subscale orderingを用いた画像の生成を行うための画像デコーダで、これまでに生成されたスライスの情報をそのメタ位置（他のスライスに対する相対的な位置）を維持しつつ用いて条件付けを行うconditional partと、それによって条件付けられながら自己回帰モデルでスライスごとの画像生成を行うdecording partの2パートによって構成されます。

更なるアーキテクチャの詳細は複雑になるため、ここでは説明を省きます（興味のある方は原論文の第3章を参照してください。）

実験結果

論文中のTable 1を以下に示します。

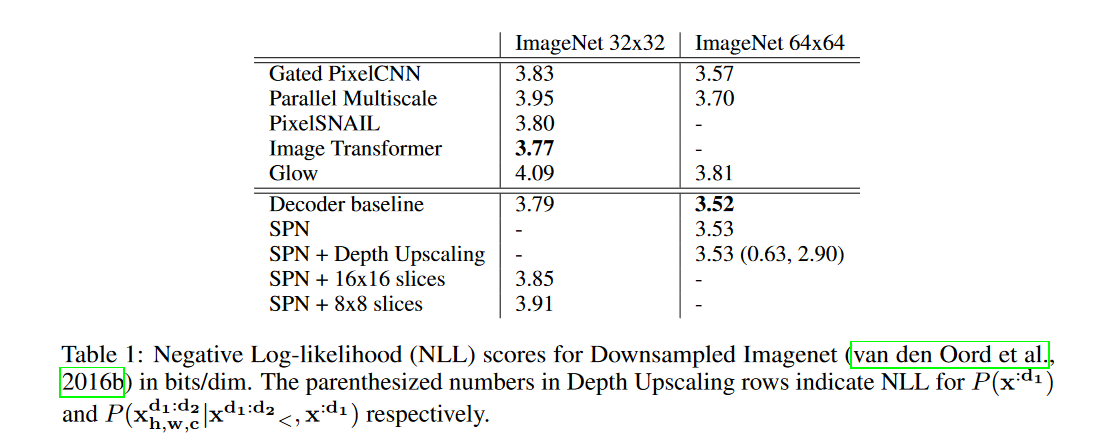
これは32×32及び64×64にダウンサンプルされたImageNetにおける結果です。
表中に示されているのは負の対数尤度（Negative Log Likelihood, NLL）なので小さい方が良いのですが、この表においては、SPNを用いていない通常のDecoder構造に対して、SPNを導入することで結果が悪化してしまっています。

これは、SPNの導入は高解像度の画像生成を目的としたものなので、32×32や64×64のように小さな画像では分割した各スライスのサイズが小さくなりすぎてしまうことによると考えられます。

実際、以下に示すTable 2やTable 3を見ると（SPNなしのモデルとの比較はありませんが）本論文での提案モデルは生成する画像が大きくなるにつれて、NLLが小さくなり、Glow²等比較対象の他モデルを大きく引き離しています。

コメント

シンプルで分かりやすい発想で大きな精度向上を成し遂げており、面白い論文でした（実装レベルのアーキテクチャは相当に複雑ですが）。
この論文はあくまで高解像度の画像生成を目的としていますが、内部的に超解像に通じる仕組みを含んでいるので、明確に超解像に適用した論文なんかも今後出てきそうです。
少し気になったのが、自己回帰モデルはその原理上生成がどうしても逐次的にならざるを得ず、高解像度の画像のように非常に高次元のものを生成しようとすると相当な時間がかかるはずです³が、論文中では特に言及されていませんでした。256×256の画像の生成、1枚にどれくらい時間かかるんでしょうか。

1. [Generative Adversarial Networks] (https://arxiv.org/abs/1406.2661) ↩

2. Glow: Generative Flow with Invertible 1x1 Convolutions ↩

3. 参考：[自己回帰モデルによるリアルタイム生成の様子] (https://github.com/PrajitR/fast-pixel-cnn) ↩