PyTorch Advent Calendar 2018 23日目の記事です。
はじめに
最近、Flow-based生成モデルがアツいです。
Flow-based生成モデルは、GANやVAE等とは異なる独立の生成モデルで、データ点に対する厳密な潜在変数及び対数尤度の計算が可能であることが特徴です。
2018年夏、非常に高精細な顔画像の生成を実現したことで話題を呼んだGlow: Generative Flow with Invertible 1x1 Convolutionsもこの系列の生成モデルに属します。(ちなみにこの論文の著者の1人はAdamやVAEでおなじみKingma氏です。強い…)

Flow-based生成モデルの流れとして、2018年12月現在ではParallel WaveNetなどが属するAutoregressive Flowベースの手法と、上述したGlowなどが属する**RealNVP**ベースの手法が主流かと思われます。
今回は後者の手法のベースになっているRealNVPについて、そのコンセプトをFlow-based生成モデルの基礎からざっと説明し、その後PyTorchを用いて簡単な2-D toy datasetを用いて実践してみます。
Flow-based生成モデルの基礎
Flow-based生成モデルは、Normalizing Flowの論文から流行り始めた生成モデルの系列です。(この論文が最初かは微妙ですが…)
Flow-based生成モデルでは、画像などの学習したい確率分布と、多次元の等方性ガウス分布等の自明な確率分布の間を繋ぐ変換を学習することを目指します。
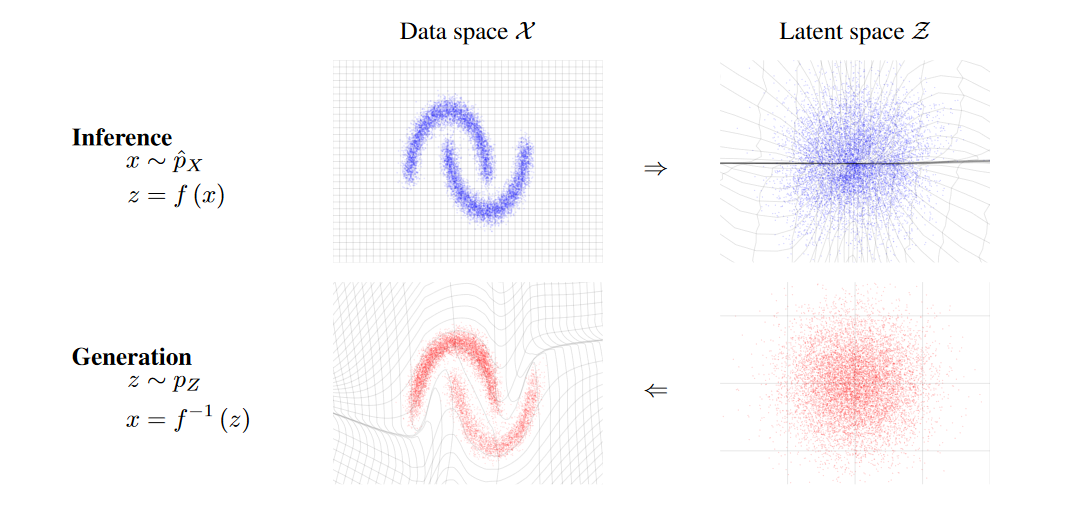
GANやVAEでも潜在変数は多次元の等方性ガウス分布に取ることが多いため、この点では同じなのですが、Flow-based生成モデルが特徴的なのは、この変換を常に逆変換可能なように構築することです。
こうすることで、変換 $f(x)$ によって画像等の訓練データ$x$を等方性ガウス分布上の点$z$に写像することができ、等方性ガウス分布上の点の確率は容易に計算できるので、訓練データの対数尤度を厳密に計算することができます。
同時に、等方性ガウス分布上の点$z$は容易にサンプルできるので、変換$f^{-1}(z)$によってこれを逆写像することで、画像等のデータを生成することができます。
このとき、対数尤度の計算においてもう1つ必要なこととして、ヤコビアンの計算があります。
変換$f(x)$ によって訓練データを等方性ガウス分布上の点$z$に写像できれば、この写像先の点の確率$p(z)$は簡単に計算できますが、ここから元の訓練データの確率$p(x)$を計算するためには、変換$f$によって発生した空間の変形分を補正してやる必要があります。
式で表すと以下のようになります。
p(x) = p(f(x))|\det(\frac{\partial f(x)}{\partial x})|
積分をするときに積分変数の変数変換(置換積分)をする場合がありますが、あのときに1次元なら係数、多次元ならヤコビアンが出てきていたのと同じ理屈です。
ここまでの話をまとめると、逆変換可能かつ、ヤコビアンの計算が容易な変換を設計してやれば、潜在変数や対数尤度の厳密な計算が可能な生成モデルを構築できるということになります。
また、必ずしも1回の変換で訓練データの確率分布と自明な確率分布の間を繋ぐ必要はありません。
逆変換可能な変換を幾つ積み重ねても全体として逆変換可能なままなので、以下の図のように1つ1つはシンプルな変換を複数個重ねて表現力を向上させ、全体の変換を構築するのが普通です。
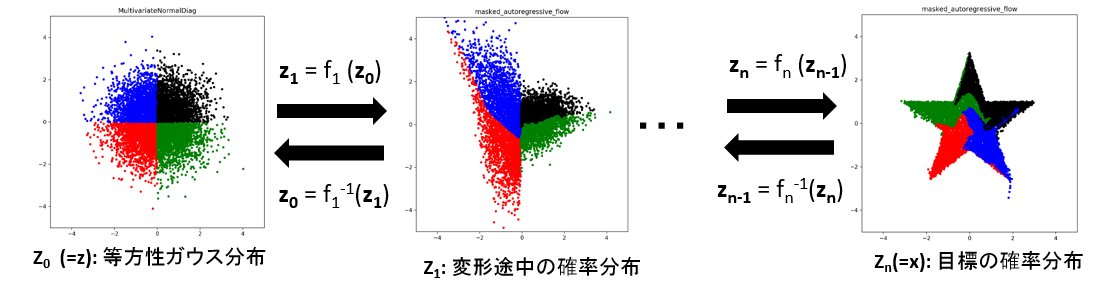
この場合の訓練データの確率の計算は、式で表すと以下のようになります。
p(x) = p(z)\prod_{i=1}^{K}{|\det(\frac{\partial z_i}{\partial z_{i-1}})|}
ここで、Kは積み重ねた変換の総数で、$z_0=x$、$z_K=z$に対応します。
実際の計算では、積を和にしたほうが扱いやすいので多くの場合対数を取ります。
\log{p(x)} = \log{p(z)} + \sum_{i=1}^{K}{\log{|\det(\frac{\partial z_i}{\partial z_{i-1}})|}}
残る問題は、これらの変換が何れも効率的に学習可能でなければならず、また多数の変換を直列に積み重ねるのは計算の並列性を損なうので、1つの変換でできるだけ大きな表現能力を持って欲しいということです。
そういった性質の良い変換を追求するために多くの研究が行われており、以下で説明するRealNVPもその1つです。
RealNVP
RealNVPは、Density estimation using Real NVPで提案されたFlow-based生成モデルの1つです。
RealNVPでは、Coupling Layerと呼ばれる変換を積み重ねて全体の変換を構築します。
以下に原論文から持ってきたCoupling Layerの図を載せます。

この図だけ見てもよく分からないので、以下で数式と合わせて説明します。
Coupling Layerでは、1つの変換を以下の式のように構築します。(図中の(a)に対応)
x_{1:d}, x_{d+1:D} = split(x) \\
y_{1:d}=x_{1:d} \\
y_{d+1:D}=x_{d+1:D} \odot \exp(s(x_{1:d})) + t(x_{1:d}) \\
y = concat(y_{1:d},y_{d+1:D})
1つの変換の入力が$x$, 出力が$y$に対応します。
まず、1つ目の式で$x$の要素を2つに分割します。
2つ目の式のように、その分割されたうちの片方$x_{1:d}$はそのまま出力にコピーしてしまいますが、この$x_{1:d}$を入力として残りの入力$x_{d+1:D}$をアフィン変換するための係数とバイアス項$s(x_{1:d})$と$t(x_{1:d})$を何らかの関数で計算します。
これを用いて3つ目の式のようにアフィン変換によって$x_{d+1:D}$を$y_{d+1:D}$に変換し、最後に$y_{1:d}$とまとめて出力とします。
Flow-based生成モデルにおける変換は全て逆変換可能である必要がありました。
上の式の逆変換は以下の形で計算できます。(図中の(b)に対応)
y_{1:d}, y_{d+1:D} = split(y) \\
x_{1:d}=y_{1:d} \\
x_{d+1:D}=(y_{d+1:D} - t(y_{1:d})) \odot \exp(-s(y_{1:d})) \\
x = concat(x_{1:d},x_{d+1:D})
ここで重要なことは、逆変換を計算するためにこれらの$s$と$t$を算出する計算を逆変換する必要はないということです。
則ち、$x_{1:d}=y_{1:d}$を入力とした$s$と$t$の計算のためには任意の関数を用いることが出来ます。
通常はここにニューラルネットワークを用います。
ニューラルネットワークは一般には逆変換可能でないので、Flow-based生成モデルの枠組みに組み込むために以上のような工夫が必要でした。
Coupling Layerの順変換のヤコビ行列は、以下のようになります。
\frac{\partial y}{\partial x}
=
\begin{bmatrix}
\frac{\partial y_{1:d}}{\partial x_{1:d}} & \frac{\partial y_{1:d}}{\partial x_{d+1:D}} \\
\frac{\partial y_{d+1:D}}{\partial x_{1:d}} & \frac{\partial y_{d+1:D}}{\partial x_{d+1:D}}
\end{bmatrix}
=
\begin{bmatrix}
\mathbb{I}_d & 0 \\
\frac{\partial y_{d+1:D}}{\partial x_{1:d}} & diag(\exp(s(x_{1:d})))
\end{bmatrix}
ここで、$\mathbb{I}_d$はd次元の単位行列で、$diag(\exp(s(x_{1:d})))$は$\exp(s(x_{1:d}))$を対角成分に持つ対角行列です。
なかなか計算が厄介そうな見た目をしています。
特に左下の成分は簡単には計算できそうにありません。
しかし、求めたいのはこのヤコビ行列の行列式であるヤコビアンで、行列式には「三角行列の行列式は対角成分の積になる」という性質があります。
よって、Coupling Layerにおけるヤコビアンは、結局$\prod_{j=d+1}^{D}{\exp{(s_{j}(x_{1:d}))}}$ という比較的分かりやすい形になります。
上述したように、実際にはこの対数を扱うことが多いので、最終的にヤコビアンの対数は$\sum_{j=d+1}^{D}{s_{j}(x_{1:d})}$という形になります。
expとlogが打ち消し合ってかなりシンプルな形になりました。
先程のアフィン変換の式で、アフィン変換の係数sを直接かけずに一旦指数を取っていた理由がここにあります。(また、対数を予測したほうが出力の変動が少なく、ニューラルネットワークとして安定して予測しやすいという理由もあります。)
Coupling Layerの説明は概ね以上です。
実際には、このCoupling Layerを複数積み重ねて全体の変換を構築します。
しかしながら、単にCoupling Layerを積み重ねても出力にそのままコピーされていた$x_{1:d}$は何も変換されないままなので、実際にはCoupling Layerを複数積み重ねて全体の変換を構築する際、間に変数の次元の順番を交換する操作を挟みます。
これは"permutation"と呼ばれます。
このpermutationの役割についてはMasked Autoregressive Flow for Density Estimationに詳しい議論があります。
簡単に要約すれば、学習したい訓練データの確率分布における変数の次元の間に複雑な依存関係がある場合、適宜変数の順番を入れ替えなければモデル化できないということです。
permutationにも色々研究の余地があり、一番分かりやすいのは変数の次元の順番を単に反転することですが、冒頭で述べたGlowではpermutationを一般化した1×1 Invertible Convolutionという操作を導入し、生成できる画像の質を大きく向上しています。
RealNVP全体としては、等方性ガウス分布への写像とヤコビアンの計算を合わせて、訓練データの対数尤度を厳密に計算し、それに基づいて負の対数尤度を最小化するように学習を行うことになります。
学習する部分は各Coupling Layerに含まれるニューラルネットワークのパラメータで、これらは通常の誤差逆伝播法の枠組みで学習が可能です。
RealNVPの基本的な説明は以上です。
説明しきれなかった事柄もありますが、それについては原論文を参照して下さい。
では、RealNVPのコンセプトを2次元のシンプルな人工データセットで試してみます。
PyTorch Advent Calendarの記事なのにずっとPyTorchの出てこない説明をしていましたが、ここでやっとPyTorchが登場します。
PyTorchで簡単にRealNVPを試してみる
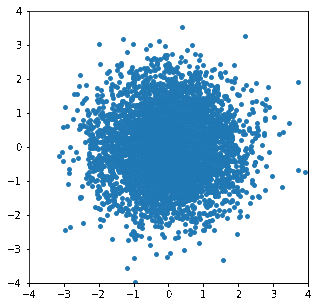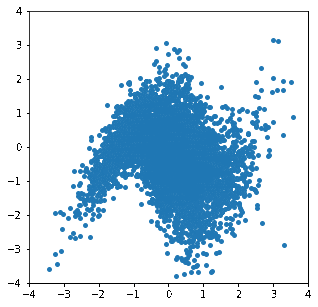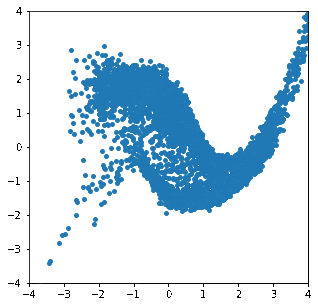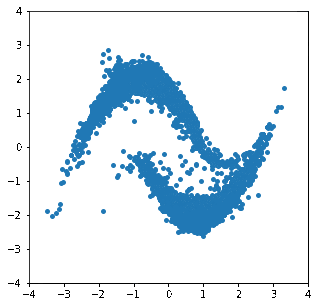
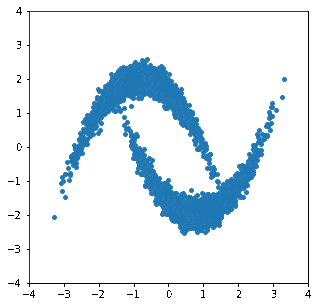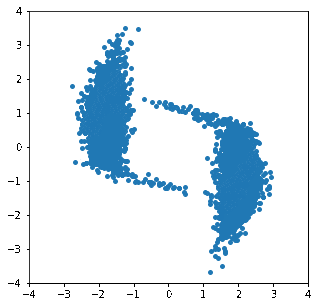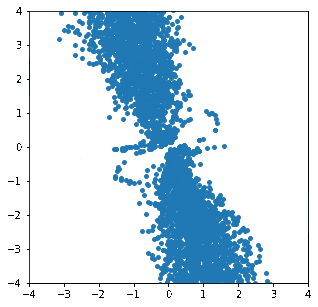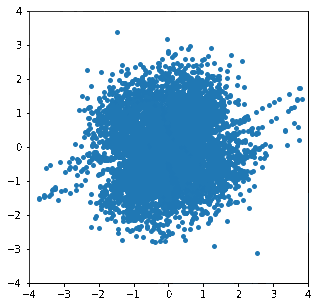
今回、RealNVPのコンセプトを2-D toy datasetで試してみるため、RealNVPの原論文にもあった2次元の"Double Moon"分布を作成しました。
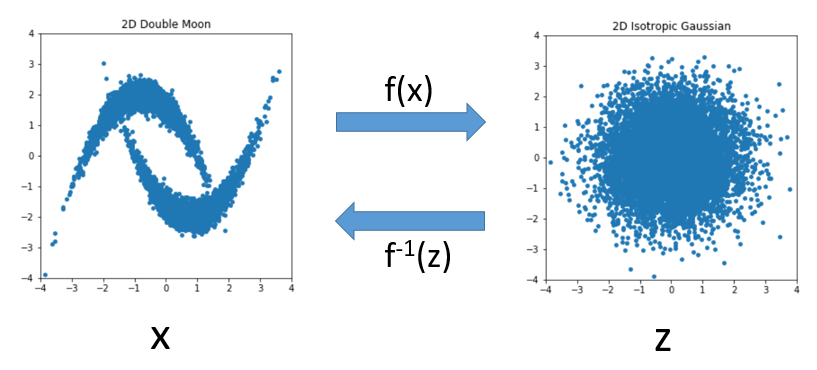
左側の"Double Moon"分布と右側の2次元の等方性ガウス分布との間の変換$f$をRealNVPの手法を用いたモデルで学習してみます。
今回の実験で用いたコード全体はGithubにあります。
今回用いたRealNVPのモデル全体を以下に示します。
class RealNVP(nn.Module):
def __init__(self, n_flows, data_dim, n_hidden):
super(RealNVP, self).__init__()
self.n_flows = n_flows
self.NN = torch.nn.ModuleList()
assert(data_dim % 2 == 0)
self.n_half = int(data_dim/2)
for k in range(n_flows):
self.NN.append(NN(self.n_half, n_hidden))
def forward(self, x, n_layers=None):
if n_layers == None:
n_layers = self.n_flows
log_det_jacobian = 0
for k in range(n_layers):
x_a = x[:, :self.n_half]
x_b = x[:, self.n_half:]
s, t = self.NN[k](x_a)
x_b = torch.exp(s)*x_b + t
x = torch.cat([x_b, x_a], dim=1)
log_det_jacobian += s
return x, log_det_jacobian
def inverse(self, z, n_layers=None):
if n_layers == None:
n_layers = self.n_flows
for k in reversed(range(n_layers)):
z_a = z[:, self.n_half:]
z_b = z[:, :self.n_half]
s, t = self.NN[k](z_a)
z_b = (z_b - t) * torch.exp(-s)
z = torch.cat([z_a, z_b], dim=1)
return z
以下各部分について細かい説明をします。
コンストラクタで、各Coupling Layerで用いられるニューラルネットワークを準備しています。
forward()メソッドが訓練データ$x$を等方性ガウス分布$z$に写像する処理に対応します。
x_a = x[:, :self.n_half]
x_b = x[:, self.n_half:]
forward処理ではまず、1つの変換の入力変数xを$x_a$と$x_b$に分割しています。
少しnotationが変わっていますが、$x_a$と$x_b$はそれぞれ前章での$x_{1:d}$と$x_{d+1:D}$に対応します。
self.n_halfにはxの次元の半分の値が入っており、次元の数が$x_a$と$x_b$で均等になるように分割しています。
s, t = self.NN[k](x_a)
x_b = torch.exp(s)*x_b + t
x = torch.cat([x_b, x_a], dim=1)
log_det_jacobian += s
次に、今考えているCoupling Layerに対応するニューラルネットワークに分割した入力の片方($x_a$)を入力し、アフィン変換の係数sとバイアスtを計算して、アフィン変換を実行しています。
その後、torch.cat()を用いて$x_a$と$x_b$を結合していますが、ここで$x_a$, $x_b$の順ではなく$x_b$, $x_a$と2つの次元の順序を入れ替えています。
これが重要で、前章で述べたpermutationに対応する部分です。
Coupling Layerのヤコビアンは$s$に対応するので、これを変換ごとに加算していきます。
本来は$s$は$x_b$と同じ次元を持ち、ヤコビアンがスカラ値になるように和を取る必要がありますが、今回は$x_b$が1次元のためそのままです。
以上の処理を重ねる変換の数だけ繰り返します。
inverse()メソッドが等方性ガウス分布$z$を訓練データ$x$に逆写像する処理に対応します。
学習はforward()メソッドのみで行い、inverse()メソッドは推論時に用います。
z_a = z[:, self.n_half:]
z_b = z[:, :self.n_half]
s, t = self.NN[k](z_a)
z_b = (z_b - t) * torch.exp(-s)
z = torch.cat([z_a, z_b], dim=1)
inverse()メソッドではforward()メソッドで行ったのと全く逆の処理を行います。
forward()メソッドで1つの変換の最後に変数の順序を入れ替えていたので、inverse()メソッドでは1つの変換の最初でスライスの分け方を変更することで変数の順序を入れ替え、変換の最後のtorch.cat()では変数の順序を特に入れ替えずに結合しています。
また、s, tはforward()と同じようにNNに分割した変数の片方を入力して求め、前章で式として示したものと同じアフィン変換の逆変換を実行しています。
RealNVPクラス内で登場したNN()ですが、以下のような2層の全結合ネットワークを用いています。
class NN(nn.Module):
def __init__(self, n_input, n_hidden):
super(NN, self).__init__()
self.fc1 = nn.Linear(n_input, n_hidden)
self.fc2 = nn.Linear(n_hidden, n_hidden)
self.fc3_s = nn.Linear(n_hidden, n_input)
self.fc3_t = nn.Linear(n_hidden, n_input)
def forward(self, x):
hidden = F.relu(self.fc2(F.relu(self.fc1(x))))
s = torch.tanh(self.fc3_s(hidden))
t = self.fc3_t(hidden)
return s, t
ここで実装上重要なのは、sを出力する際に出力層の活性化関数としてtorch.tanh()やtorch.sigmoid()等の出力の値域を制限する関数をかけることです。
こうしておかないとたちまち学習が発散し、nanのみを延々と吐き出すネットワークが完成します。(始めはこれで結構ハマりました。)
後はいつも通りDataLoaderを用意し、ミニバッチ確率的勾配降下法で学習します。
今回は変換の数(RealNVPクラスのn_flows)は4とし、各NNの隠れ層の次元数は256としました。
sample_z, log_det_jacobian = net(sample_x)
loss = -1 * torch.mean(z.log_prob(sample_z) + log_det_jacobian)
loss.backward()
optimizer.step()
学習ループ中の重要な部分のコードを上に示しました。
zはtorch.distributions.multivariate_normal.MultivariateNormalクラスのインスタンスで、2次元の等方性ガウス分布として用意して事前にインスタンス化しておきました。
zのlog_prob()メソッドを用いて訓練データsample_xから写像されたsample_zの対数確率を評価しています。
後はヤコビアンのlogを加算して平均を取ることで元の訓練データsample_xの対数尤度が求まります。
PyTorchでは基本的にロス関数を最小化するように学習を実行するため、最後に-1をかけて対数尤度の最大化を負の対数尤度の最小化に置き換えておきます。
学習完了後、inverse()メソッドを用いて等方性ガウス分布から新しくサンプルしたデータを"Double Moon"分布へ写像した結果を真の分布と並べて以下に示します。
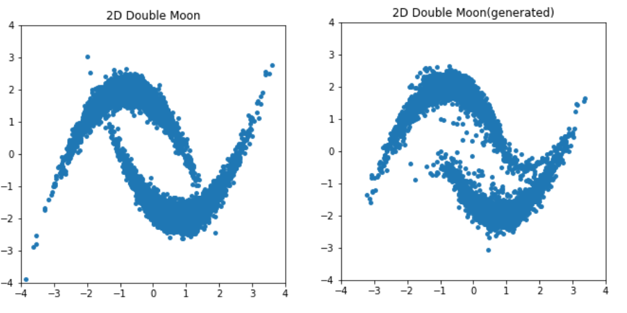
分布の端のデータ数の少ない部分はちょっと怪しいですが、概ね目標の確率分布にサンプルを写像できていることが分かります。
forward()メソッドを用いて"Double Moon"分布から等方性ガウス分布へ写像した結果の方も見てみます。
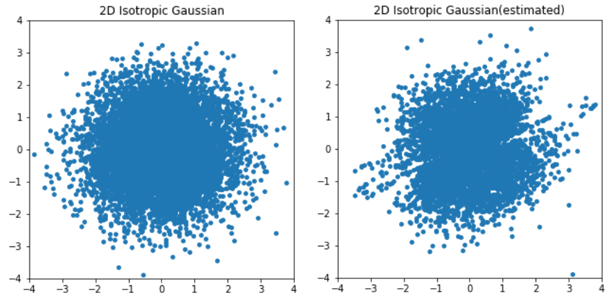
多少分布が2つに分かれていたときの名残が残っていますが、こちらは概ね上手くいっているようです。
RealNVP()クラスでは、forward()メソッドとinverse()メソッドに関して、通過する変換の数を引数として与えることで変換途中のサンプルを出力できるようにしてあります。
これを用いて変換が徐々に進んでいく様子をgif画像にしてみました。
徐々に分布が変形し、目標の分布に近づいていく様子が見て取れます。
おわりに
今回は2次元の非常に簡単なデータセットを作成してRealNVPのコンセプトを実践してみましたが、RealNVPの方針は画像等の高次元のデータに対してもスケールすることが可能です。
今回はRealNVPにフォーカスしており、Flow-basedモデルについての説明はかなりあっさりやってしまったので、より詳しく知りたい方は以下の参考リンク先をご覧ください。