機械学習の数理24日目の記事です。本稿ではgraph convolutional network(GCN, グラフ畳み込みネットワーク)の基本的な理論について解説を試みたいと思います。GCNの応用だとか、変種だとか、については特に述べません。
グラフ畳み込みを知らない方、あるいはグラフ畳み込みの数式は理解しているけどもイマイチ理解できていない方を想定しています。ただし線形代数とFourier(フーリエ)変換(実質、無限次元線形代数)の基本は知っているものとします。実際、数式だけ理解するなら、この2つさえ知っていれば十分なのですが、理論的背景(特に信号処理)についてきちんと踏み込んでいるものは、ほとんど無さそうだったので、今一度振り返るべく文章化してみました。
ちなみにグラフ畳み込みにおいて重要な役割を果たすグラフLaplace作用素は、物理学において、tight-binding模型のHamiltonianと呼ばれるものと等価です。特に固有値はエネルギースペクトルと呼ばれ、固有ベクトルはその波動関数に対応します。
また機械学習の文脈では、スペクトル・クラスタリングと密接に関係しています。
なお、本稿の前半では2乗可積分な関数空間$L^2(\mathbb{R})$では閉じない話も出てくるため、数学的厳密性はかなり犠牲にしています。しかしながら、本質的な部分は残していますので、機械学習の数理的側面を語る上では十分だと思われます。
コメント
この記事は、「畳み込みの局所性と多項式の次数」「グラフウェーブレット・Chebysheff多項式近似」「グラフ粗視化とクラスタリング」などのパートも予定していましたが、執筆者が疲れてしまったので、一旦ここまでとします。内容は閉じているので問題ありません。気が向いたら加筆いたします。
参考文献(随時増える可能性あり)
-
Thomas N. Kipf, Max Welling, "Semi-Supervised Classification with Graph Convolutional Networks", arXiv:1609.02907, ICLR 2017
-
Michaël Defferrard, Xavier Bresson, Pierre Vandergheynst, "Convolutional Neural Networks on Graphs with Fast Localized Spectral Filtering", arXiv:1606.09375, NIPS 2016
-
Mathias Niepert, Mohamed Ahmed, Konstantin Kutzkov, "Learning Convolutional Neural Networks for Graphs", arXiv:1605.05273, ICML 2016
-
David K Hammond, Pierre Vandergheynst, Rémi Gribonval, "Wavelets on Graphs via Spectral Graph Theory", arXiv:0912.3848, Applied and Computational Harmonic Analysis Volume 30, Issue 2, March 2011, Pages 129-150
-
Inderjit S. Dhillon ; Yuqiang Guan ; Brian Kulis , "Weighted Graph Cuts without Eigenvectors A Multilevel Approach", IEEE Transactions on Pattern Analysis and Machine Intelligence ( Volume: 29 , Issue: 11 , Nov. 2007 )
-
Mikhail Belkin, Partha Niyogi, "Towards a theoretical foundation for Laplacian-based manifold methods", Journal of Computer and System Sciences
Volume 74, Issue 8, December 2008, Pages 1289-1308
連続空間上の畳み込み
グラフ上の信号が与えられた時に、『畳み込み』という操作をどう特徴づけるか、というのが本来考えたい問題ですが、その前にまずは、連続の場合の信号処理について捉え直してみましょう。
そこで得られた抽象的視点を元に、グラフ上の畳み込みの定義へ戻ってくる事にします。
窓関数(フィルター)と畳み込み
まずは連続空間(例えば$n$個の実数の集まりを表す$\mathbb{R}^n$)上の関数 $f(x)$と$g(x)$の畳み込みと呼ばれる操作が、次のように定義される事を思い出します。1
\begin{align}
(f \ast g)(x) := \int_{\mathbb{R}^n} dy^n\; f(y)g(x-y)
\end{align}
ただし信号処理の文脈では、入力信号$s(x)$と窓関数あるいはフィルター $\phi(x)$を非対称に扱い、特に2変数関数と見なした場合、核(カーネル) $\phi_K(x,z)$と呼びます。2
\begin{align}
o(x) = (\phi \ast s)(x) := \int_{\mathbb{R}^n} dy^n\; \phi(y)s(x-y) = \int_{\mathbb{R}^n} dz\; \phi_K(x,z)s(z)
\end{align}
以降、混乱のない限り、入力信号$s$に対し、対応する出力信号を$o$と表す事にします。
なおこの操作は、直感的には、入力信号$s(x)$の中に含まれている、$\phi(x)$という形の信号を抜き出す事に対応します。
Gaussianフィルターによる畳込み
具体的な窓関数として、Gauss関数を選んだ場合を考えてみましょう。
すなわち $\phi(x)$として
\begin{align}
\phi(x-z) = H_{t}(x,z) := \dfrac{1}{t^{n/2}} \exp\left[ -\dfrac{\pi |x-z|^2}{t} \right]
\end{align}
と取ります。ここで$\mathbb{R}^n$上の$L^2$-ノルム(Euclide距離)の2乗
\begin{align}
|x-z|^2 = \sum_{i=1}^{n} (x_i-z_i)^2
\end{align}
を導入した事と、正規化条件
\begin{align}
\int_{\mathbb{R}^n} H_{t}(x,y) = 1
\end{align}
を満たす事に注意してください。また$\sqrt{t}=:\sigma$ をこの窓関数(フィルター)のスケールと呼ぶ事にします。
さて、この窓関数はGaussフィルターや熱核とも呼ばれますが、一体どのような働きをするのでしょうか?
まず入力信号 $s$として、$x$に依らない定数$c$の場合を考えてみると、定義から明らかなように、出力信号も定数であり、正規化条件から $o(x)=c$です。よって、定数信号は畳み込みに対し、安定な関数です。実際に、後の議論から分かるように、このGaussフィルターを何度もかけると、定数信号以外しか残りません。
次に、変動が緩やかな関数と激しい関数をそれぞれ考えてみましょう。2018年の人類水準では、気軽に高次元のグラフを可視化できないので、ここでは$n=1$の場合を念頭に置きます。
下図(左)で示したように、Gaussフィルター(青色の実点線)のスケール $\sigma$よりも大きなスケールで変動する緩やかな関数(緑の実線)は、Guassフィルターが盛り上がっている領域(図中の色がついた領域)でだいたい定数なので、畳み込んでもあまり変わらないと考えられます。(フィルターと信号の積が赤の点線)
上図(右)のように一方でGaussフィルターのスケール$t$よりも小さなスケールで変動する激しい関数(緑の実線)ではどうなるでしょうか?激しい振動で、互いに積分への寄与がキャンセルして、平均の値しか残らず(フィルターと信号の積が赤の点線で、積分値が畳み込み結果の中心での値を与える)、平滑化される事が期待されます。
以降、もう少し詳しく見ていきましょう。
Gaussフィルターの数値実験
理論的解析を行う前に、Gaussフィルターによる畳み込みの数値実験をしてみましょう。
ここでも可視化と計算量の都合から$n=1$に話を限定します。
from scipy import signal
import numpy as np
N_samples = 1000
L = 25
beta = 0.15
# 入力信号
y_original = np.cos(beta * np.linspace(0,L,N_samples)**2)
# スケール
std = 50
# Gaussフィルターを定義
gaussian_flter = signal.gaussian(N_samples, std)
# フィルターの正規化
gaussian_flter = gaussian_flter / gaussian_flter.sum()
# 畳み込み結果を出力信号として得る
y_filtered = signal.convolve(y_original, gaussian_flter, mode='same')
ここでGaussフィルターのスケール $\sigma$を大きく変えていった時の、出力信号の変化を表した結果が以下になります。
ここで、左図はGaussフィルターの概形、右図は出力信号です。見やすさのため、左右でスケールは変えている事に注意してください。
Guassフィルターのスケール $\sigma$を大きくする程、高周波成分が落ちていく事が見て取れます。ちなみに、こういう低周波数のみ通すフィルターは一般にlow-passフィルターと呼ばれています。
Fourier分解と単一周波数成分のGaussフィルターによる畳み込み
先の考察・実験を数式で表してみましょう。周波数毎に分解する手法として、Fourier変換がありますね。なお、Fourier変換の基本的な事項はここでは説明しません。
これにより、$n$次元空間 $\mathbb{R}^n$上の関数 $f(x)$は、同じ次元$n$を持つ周波数空間(あるいは波数空間、スペクトル空間、双対空間とも呼ぶ)上の関数 $\hat{f}(k)$を用いて、
\begin{align}
f(x) = \int_{\mathbb{R}^n} \dfrac{dk^n}{(2\pi)^n}\; \hat{f}(k) e^{-ik \cdot x}
\end{align}
と積分で展開されるのでした。ここで、
\begin{align}
k \cdot x := \sum_{i=1}^{n}k_ix_i
\end{align}
として内積を表しました。
さて、$e^{\mp ik \cdot x} ; (k \in \mathbb{R}^n)$は周波数空間の基底と見なせますが、$\cos(k \cdot x)$と$\sin(k \cdot x)$への基底に組み替える事もできます。さらに$\cos(k \cdot x)$と$\sin(k \cdot x)$は$x$の平行移動により互いに移り変わるため、$\cos(k \cdot x)$のみに着目しましょう。すなわち入力信号が$\cos$関数の場合 $s(x) = \cos(k \cdot x)$を考えましょう。ちなみにこの時、$\hat{s}(\ell) = \frac{1}{2}(2\pi)^n (\delta(\ell-k) + \delta(\ell+k))$で、$\delta(\ell)$はDiracの$\delta$-関数で点スペクトラムとして表せます。
すると、畳込みの結果は
\begin{align}
o(x) &=
\int_{\mathbb{R}^n} dy^n\; H_t(y) \cos(k \cdot (x-y)) \\
&= \exp\left[ - \dfrac{k^2 t}{4\pi} \right] \cos(k \cdot x)
= e^{ - \frac{k^2 \sigma^2}{4\pi} } s(x)
\end{align}
となります。ここで省略記号$k^2 := |k|^2 = k \cdot k$は$k$の$L^2$-ノルムの2乗です。
一言だけ導出について補足しておきますと、$\alpha \in \mathbb{R}_{>0}$(正の実数)と$\beta \in \mathbb{C}^n$($\mathbb{C}$は複素数の集合(あるいは体)を表します)に対する次の等式
\begin{align}
\int_{\mathbb{R}^n} dy^n\; \exp\left[ - \alpha y^2 + \beta \cdot y \right]
=
\exp\left[ \dfrac{\beta^2}{4\alpha} \right] \sqrt{\dfrac{\pi}{\alpha}}
\end{align}
を使用しました。$\beta \cdot x$は以前の定義式をそのまま複素数に拡張したものになります。
上の式が意味する所は、単一の三角関数の入力信号をGaussフィルターに通しても、その関数形は変わらずただ振幅のみが減衰します。その時の減衰の強さ($e$の指数)は $k^2 \sigma^2$と、周波数$k$の2乗とGaussフィルターのスケール$\sigma$の2乗にそれぞれ比例しています。よって、高周波数になる程、あるいはGaussフィルターのスケールが大きい程(拡がっている程)、減衰が激しくなり、先に見た高察や結果を再現します。
畳み込み定理
さて、一般の信号ではどうでしょうか?
畳み込みを行う空間上の積分(変数$y$での積分)と波数空間上の積分(変数$k$での積分)は入れ替えられる、とすると、
\begin{align}
o(x) &=
\int_{\mathbb{R}^n} dy^n\; H_t(y)\; s(x-y)
=
\int_{\mathbb{R}^n} dy^n\; H_t(y)\; \int_{\mathbb{R}^n} \dfrac{dk^n}{(2\pi)^n}\; \hat{s}(k)\; e^{-ik \cdot (x-y)}
\\
&= \int_{\mathbb{R}^n} \dfrac{dk^n}{(2\pi)^n}\; \hat{s}(k)\; e^{-ik \cdot x}
\int_{\mathbb{R}^n} dy^n\; H_t(y)\; e^{ik \cdot y}
=
\int_{\mathbb{R}^n} \dfrac{dk^n}{(2\pi)^n}\; \hat{s}(k)\;\hat{H}_t(k)\; e^{-ik \cdot x}
\end{align}
と計算できます。これは波数空間上で見ると、
\begin{align}
\hat{o}(k) = \hat{s}(k)\;\hat{H}_t(k)
\end{align}
となり、Gaussフィルター $H_t(x)$のFourier変換関数 $\hat{H}_t(k)$の単なる掛け算操作になっています。こっちの世界では畳み込みという積分を伴う演算が、あっちの世界では掛け算という単純な作用に落ちてしまい、何とも不思議です。この主張は、Fourier変換に対する畳み込み定理と呼ばれているものに相当します。3
なお、$\hat{H}_t(k)$は先に見たように、
\begin{align}
\hat{H}(k) = \exp\left[ -\dfrac{k^2 t}{4\pi} \right]
\end{align}
で与えられ、減衰ファクターに対応しているわけです。
また$k$依存性に着目しますと、$\hat{H}_t(k)$の掛け算は、おおよそ$-\frac{1}{\sigma}$から$\frac{1}{\sigma}$までの低周波数領域のみ取り出し、その外側(高周波側領域)はほぼ0の値をかける操作に対応し、やはり低周波を通過させるフィルターとなります。
ちなみに$k$をシフトする事で、通す周波数領域を変えられ、逆Fourier変換が対応する畳み込みフィルターとなるわけです。
結論として、激しく振動する信号は大きく減衰させる、というのがGaussフィルターによる畳込みの特徴である、と事が言えました。より一般のフィルターについて、この主張は成り立ちませんが、少なくともよく通す周波数領域と、大きく減衰させる周波数領域が存在する、という事実は変わりません。
これはグラフ上の畳込みを定義する上で、重要な考え方になる事を後で見ていきます。
Laplace作用素による表現(熱核)
さて一般の信号に対するGaussフィルターによる畳み込み結果は、周波数空間上でのGauss関数の掛け算で書ける事を見てきました。実はこの表式から、さらに畳み込みを使わない表式を得る事ができます。
そのために次の等式が成り立つ事に注意しましょう。
\begin{align}
\exp\left[ -\dfrac{k^2 t}{4\pi} \right] \exp\left[-ik \cdot x\right]
=
\exp\left[ \dfrac{t}{4\pi} \sum_{i=1}^{n} \dfrac{\partial^2}{\partial x_i^2} \right] \exp\left[-ik \cdot x\right]
\end{align}
微分演算子を$e$の指数に乗っけた表式に馴染みのない方もおられますが、今の場合、Taylor展開で定義されていると捉えてください。この微分演算子はLaplace(-Beltrami)作用素と呼ばれ、通常 $\Delta$という記号を使用します。定義は
\begin{align}
\Delta := -\sum_{i=1}^{n} \dfrac{\partial^2}{\partial x_i^2}
\end{align}
です。4
よって、任意の入力信号 $s(x)$の、Guassフィルターによる畳み込み結果である出力信号 $o(x)$は
\begin{align}
o(x)
&=
\int_{\mathbb{R}^n} dy^n\; H_t(y) s(x-y)
=
\int_{\mathbb{R}^n} \dfrac{dk^n}{(2\pi)^n}\; \hat{s}(k)\;\exp\left[ -\dfrac{k^2 t}{4\pi} \right] \exp\left[-ik \cdot x\right] \\
&=
\exp\left[ \dfrac{t}{4\pi} \Delta \right]
\int_{\mathbb{R}^n} \dfrac{dk^n}{(2\pi)^n}\; \hat{s}(k)\; \exp\left[-ik \cdot x\right]
=
\exp\left[ -\dfrac{t}{4\pi} \Delta \right] s(x)
\end{align}
すなわち
\begin{align}
o(x)
=
\exp\left[ -\dfrac{t}{4\pi} \Delta \right] s(x)
\end{align}
と。Gaussフィルターによる畳込みに対しては、Laplace作用素の指数関数で表現できる事が分かりました。これより、グラフ上の周波数に対応する概念を特徴づける上で、微分作用素を起点とすればいい、という観察結果が得られたとも言えます。
最後におまけですが、上の出力信号 $o(x)$を$t$の関数とみなし、微分してみましょう。すると
\begin{align}
\dfrac{\partial}{\partial t}o(x)
=
-\dfrac{1}{4\pi}\Delta o(x)
\end{align}
という微分方程式が得られますが、これは熱拡散方程式と呼ばれるものです。その名のとおり、(一様・等質な物質上の)温度分布が$s(x)$で与えられた時に、熱が時刻$t$と共に拡散していく現象を近似的に記述する方程式です。
グラフ上の畳込み
グラフ上の畳込みに入る前に、グラフに関係する用語を整理しておきます。
グラフは、ノード(頂点)の集合$\mathcal{V}$とエッジ(頂点を結ぶ線分)の集合$\mathcal{E}$から構成されます。特にここでは、ノードの数が有限で、エッジの向きが存在しない有限な無向グラフのみを考察対象とします。
またエッジは、ノードのペア$e=(v_1,v_2)=(v_2,v_1)$ ($v_1, v_2 \in \mathcal{V}$ただし$v_1 \neq v_2$)で一意に指定されるとし、さらに各エッジには正の実数の重み$w_e > 0$が割り当てられているとします。
この時、グラフ上の信号 $f$はノードの集合から実数$\mathbb{R}$への写像 $f : \mathcal{V} \longrightarrow \mathbb{R}$で与えられます。
また各ノードに、$1,2,\ldots,N$と番号を割り振るが事ができます。ここで$N$は全ノード数です。つまり$i$番目のノード$v$に対して、$N(i)=v$を満たす(逆)ナンバリング関数$N$を導入します。このナンバリング関数を用いて、重み行列を
W_{ij} :=
\begin{cases}
w_{e} \quad \exists e = (N(i),N(j)) \\
0 \quad {\rm otherwise}.
\end{cases}
つまり$i$番目のノードと$j$番目のノードを結ぶエッジ$e$が存在する場合に、重み$w_e$を$ij$成分に割り当て、存在しない場合は$0$を割り当てています。
最後にノード$v$の(1-)近傍$N_v$を、
N_{v} :=
\{ w \in \mathcal{V} \;|\; \exists e = (v,w) \}
で定めましょう。要するに、$v$と連結している$v$以外のノードの集合です。
以下、適当な有限ノード無向グラフを1つ固定して議論を進めます。
離散近似によるグラフLaplace作用素の導出
さて、前節の議論からグラフに対してもFourier変換を定義できれば良さそうですが、そのためにはLaplace作用素のグラフ版を定義できれば良さそうです。Laplace作用素を離散化するために、グラフはある連続なEuclide空間 $\mathbb{R}^d$に埋め込まれ、グラフ上の信号も連続的な空間上で微分可能な関数として定義されているとしましょう。すなわちグラフ上の$i$番目のノードは、その中の点$x^{(i)} \in \mathbb{R}^d$に対応し、信号は $f(x^{(i)})$で与えられます。
ただし、各ノードの近傍には、連続空間の次元$d$よりも大きなノードが存在する、と仮定しておきます。
さて、Laplace作用素を信号に掛けた時の、$i$番目のノードにおける値 $(\Delta f)(x_i)$を、グラフ上の信号だけで表現する事を考えましょう。そのためには、$i$番目のノードの近傍$N_i$に属する$j$番目のノードをTaylor展開してみます。
\begin{align}
f(x^{(j)}) = f(x^{(i)}) + (\nabla f)(x^{(i)}) \cdot a^{(ij)} + (a^{(ij)})^T \cdot (H f)(x^{(i)}) a^{(ij)} + \mathcal{O}(a^3).
\end{align}
ここでたくさん記号を導入したので、一つずつ説明します。
まず$a^{(ij)} := x^{(j)} - x^{(i)}$という相対ベクトルを定義し、さらに$a_{ij}$のノルムの典型的な値を$a$と書きました。右辺最後の項$\mathcal{O}(a^k)$は$a$を$0$に近近づけた際の収束の速さが、$a^k$程度の項を表す(同一視した)記号です。
$\nabla f$は$f$の勾配ベクトルで、各成分が$\frac{\partial}{\partial x_p}f(x) ;;(p=1,2,\ldots,d)$となります。最後に、$Hf$ですが、これは$f$のHesse行列またはHessianと呼ばれ、$pq$成分が2階微分$\frac{\partial^2}{\partial x_p \partial x_q}f(x)$で与えられます。
さてここから線形和を取って、Laplace作用素の部分だけ抜き出す事を考えます。天下り的ですが、次の性質を満たす重み$w^{(ij)}$が存在すると仮定します。
- $j \in N_i$の時のみ、$w^{(ij)} > 0$ : $i$と$j$をつなぐエッジが存在するなら重みが存在
- $w^{(ij)} = w^{(ji)}$ : 重みの対称性
- $\displaystyle \sum_{j \in N_i} w^{(ij)} a^{(ij)}_p = 0$ : 1階微分が消える
- $\displaystyle \sum_{j \in N_i} w^{(ij)} a_p^{(ij)} a_q^{(ij)} = \delta_{pq}$ : $\delta_{pq}は$p=q$の時のみ$1$、それ以外$0$を表すKronecker記号で、$Hessianから対角成分へ射影を行う働きをする
この時、
\begin{align}
\sum_{j \in N_i} w^{(ij)} f(x^{(j)}) &= \sum_{j \in N_i} w^{(ij)} f(x^{(i)}) + (\nabla f)(x^{(i)}) \cdot \sum_{j \in N_i} w^{(ij)} a^{(ij)} \\
& \qquad + \sum_{j \in N_i} w^{(ij)} (a^{(ij)})^T \cdot (H f)(x^{(i)}) a^{(ij)} + \mathcal{O}(a^3) \\
&= \sum_{j \in N_i} w^{(ij)} f(x^{(i)}) - (\Delta f)(x^{(i)}) + \mathcal{O}(a^3)
\end{align}
となり、$a^3$項を無視すると、
\begin{align}
(\Delta f)(x^{(i)}) \sim \sum_{j \in N_i} w^{(ij)} f(x^{(i)}) - \sum_{j \in N_i} w^{(ij)} f(x^{(j)})
\end{align}
という近似式を得ました。ちなみに、1次元上に等間隔にノードが並んだグラフに対しては、よく知られた近位式
\begin{align}
\dfrac{d^2}{dx^2}f(x) \sim
\dfrac{f(x+a) + f(x-a) - 2 f(x)}{a^2}
\end{align}
が得られます。
以上で、グラフ上の信号でのみの表現が得られたので、グラフが埋め込まれた連続空間の存在は忘れてしまいましょう。
グラフの重み$w$は、連続空間から定めましたが、グラフそのものに割り当てられた内在的な量だと思う事にします。5
すなわち$i$番目と$j$番目のノードをつなぐエッジに対し、重み$W_{ij}=W_{ji} > 0$が割り当てられるとしましょう。また$i$番目の対角成分が $\sum_{j} W_{ij}$で与えられる対角行列$D$を導入しましょう。
すると、グラフLaplace作用素$L$は
\begin{align}
L := D - W
\end{align}
で与えられます。ただし解析上も応用上も、正規化されたLaplace作用素
\begin{align}
\mathcal{L} := D^{-1/2} L D^{-1/2} = I - D^{-1/2}WD^{-1/2}
\end{align}
もよく用いられます。これは一般に$L$の固有値は$0$から$\infty$の範囲(正確には$\infty$は含まない、つまり上に非有界)を取れますが、上のように正規化する事で、次節で分かるように固有値の範囲を$0$から$2$と有限の範囲を取るためです。2つの固有ベクトルは、$D^{1/2}$で移り変わるので、$L$と$\mathcal{L}$は本質的に同じ情報を持ちます。
グラフFourier変換
ここまで来れば後は簡単な線形代数の問題です。$W_{ij} = W_{ji}$より$W$は実対称行列であり、$D$も実対角行列なので対称であるから、$L$も実対称行列です。よって、直交行列$U$による対角化が可能となり、$\Lambda$をその対角化行列とすると、
\begin{align}
L = U\Lambda U^T
\end{align}
です。ここで$\Lambda$の対角成分は、固有値になりますが、$aa$成分を$\lambda_a$とおけば、$a<b$に対し、$\lambda_a <= \lambda_b$を満たすように選ぶ事が可能です。そしてこの$\lambda$が連続空間では$k^2$に対応するわけです。よって、この行列 $U$による変換はグラフFourier変換と呼ばれます。
さて、上の式を書き直すと、
\begin{align}
\sum_{j} L_{ij}U_{ja} = \lambda_a U_{ia}
\end{align}
とも書けます。つまりグラフの$i$番目のノードの信号をベクトルの$i$番目の成分と解釈し、第$i$成分が$U_{ia}$で与えられるベクトルあるいは信号$u_a$は、グラフLaplace作用素の、固有値 $\lambda_a$の固有ベクトルとなっています。この$u_a$は、連続空間では$e^{ikx}$または$\cos(kx+\theta)$に対応しています。実際に並べてみると、左は(有限次元の)行列の作用、右は微分演算子の作用ですが、同じ形式をしていますね。
\begin{align}
L u_a = \lambda_a u_a
\qquad
\Delta \cos(kx) = k^2 \cos(kx).
\end{align}
これ以降、$u_a$を基底とする場合、周波数空間の代わりにスペクトル空間と呼ぶ事にしましょう。
少し寄り道
ちなみに空間の離散化は、周波数空間あるいはスペクトル空間の観点からは固有値に上限を導入すること(数学の言葉では上に有界である、あるいは物理学の言葉では紫外カットオフを入れる、と言います)に対応しています。一方で、空間の拡がりを抑える事(数学的に言えばコンパクト化)は、周波数空間あるいはスペクトル空間の観点からは固有値の離散化(数学では離散スペクトラム、物理学では赤外カットオフ、とも言います)に対応しています。ここで、元の信号が済む空間と、周波数・スペクトル空間の関係は相補的になっているわけですが、これは双対性という概念に結びついています。
グラフ上のLaplace作用素の性質
ここではグラフLaplace作用素$L$の満たすべき性質について、幾つか見ていきましょう。
まずグラフ上の任意の信号$f$に対し、
\begin{align}
f^T Lf
&=
\sum_{i,j=1}^{N} f_i L_{ij} f_j
=
\sum_{i=1}^{N} \left( \sum_{j=1}^{N} W_{ij} \right) f_i^2
-
\sum_{i.j=1}^{N} W_{ij} f_i f_j \\
&=
\sum_{i.j=1}^{N} W_{ij} \dfrac{ f_i^2 + f_j^2 - 2f_i f_j }{2}
=
\dfrac{1}{2}\sum_{i.j=1}^{N} W_{ij} ( f_i - f_j )^2 \ge 0
\end{align}
より$W_{ij} \ge 0$が満たされる限り、非負である事が言えます。特に等号成立は、ノード$i$と$j$が隣接している場合に信号の値が等しい($f_i = f_j$)時、すなわち連結された各領域上で定数である時のみに限る事も分かりますね。
またスペクトル空間での信号$g := U^T f$を導入して、
\begin{align}
f^T Lf = g^T \Lambda g
\end{align}
が成り立つ事から、固有値は非負である事が言えます。さらに上の等号成立条件から、ゼロ固有値に対応するグラフ固有ベクトルは、一つの連結グラフを選び、その上でグラフ信号が$0$でない定数値であるようなもので与えられます。これからゼロ固有値の縮退度は、連結成分の数に等しい事も言えます。
最後に、正規化されたLaplace作用素$\mathcal{L}=I - D^{-1/2}WD^{-1/2}$の固有値は、$[0,2]$の間に有る事を証明しましょう。単位行列は、全ての非零ベクトルに対し、固有値$1$の固有ベクトルである事から、これは$D^{-1/2}WD^{-1/2}$の任意の固有値が$[-1,1]$の中に存在する事と同値です。任意の信号$f$に対して、$f':=D^{-1/2}f$として、
\begin{align}
\dfrac{f^TD^{-1/2}WD^{-1/2}f}{f^Tf}
=
\dfrac{f'^TWf'}{f'^TDf'}
\end{align}
が成立します。この量は固有値の最小値$\lambda_{\rm min}$と最大値$\lambda_{\rm max}$の間の閉区間$[\lambda_{\rm min},\lambda_{\rm max}]$に値を取る事に注意すると、
\begin{align}
-\; f'^TDf' \le f'^TWf' \le \; f'^TDf'
\end{align}
を示す事と同値です。これは$W$の正定値正と同様の計算で示す事ができます。実際に、
\begin{align}
\sum_{i,j} W_{ij}f_i'f_j'
\pm
\sum_{i,j} W_{ij}f_i'f_i'
=
\pm \dfrac{1}{2}\sum_{i,j} W_{ij}(f_i'-f_j')^2
\gtrless 0
\end{align}
より、上式が成り立つ事が分かりますので、正規化されたLaplace作用素は、文字通りその固有値が正規化されちる事が示されました。
グラフLaplace作用素の固有ベクトルの例
重みが次の式で与えられるグラフを考えてみます。
\begin{align}
W=
\left[\begin{array}{ccccccccccc}0 & 1 & 1 & 2 & 0 & 1 & 2 & 0 & 0 & 0 & 0\\1 & 0 & 0 & 0 & 0 & 2 & 0 & 2 & 1 & 0 & 1\\1 & 0 & 0 & 0 & 2 & 0 & 0 & 0 & 0 & 3 & 0\\2 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 3 & 2\\0 & 0 & 2 & 1 & 0 & 3 & 0 & 0 & 0 & 0 & 1\\1 & 2 & 0 & 0 & 3 & 0 & 0 & 0 & 2 & 0 & 0\\2 & 0 & 0 & 0 & 0 & 0 & 0 & 2 & 0 & 3 & 0\\0 & 2 & 0 & 0 & 0 & 0 & 2 & 0 & 3 & 0 & 0\\0 & 1 & 0 & 0 & 0 & 2 & 0 & 3 & 0 & 3 & 0\\0 & 0 & 3 & 3 & 0 & 0 & 3 & 0 & 3 & 0 & 0\\0 & 1 & 0 & 2 & 1 & 0 & 0 & 0 & 0 & 0 & 0\end{array}\right]
\end{align}
また等価ですが、エッジと重みの情報で表現すると以下のようになります。
> edges
[(5, 8), (0, 5), (1, 7), (6, 9), (4, 5), (4, 10), (2, 4), (0, 6), (6, 7),
(0, 1), (1, 8), (3, 10), (7, 8), (1, 5), (3, 4), (1, 10), (0, 3), (0, 2),
(2, 9), (8, 9), (3, 9)]
> weights
[2.0, 1.0, 2.0, 3.0, 3.0, 1.0, 2.0, 2.0, 2.0, 1.0, 1.0, 2.0, 3.0, 2.0,
1.0, 1.0, 2.0, 1.0, 3.0, 3.0, 3.0]
さて、ここからnetworkxというpythonライブラリを用いてグラフの可視化を行います。6
import networkx as nx
g = nx.Graph()
g.add_weighted_edges_from([ (e[0],e[1],w) for e,w in zip(edges, weights)], weight='weight')
np.random.seed(3)
pos = nx.spring_layout(g)
ec = nx.draw_networkx_edges(g, pos, alpha=0.5, width=weights)
nc = nx.draw_networkx_nodes(g, pos, nodelist=g.nodes(), with_labels=False, node_size=30)
すると先の重みで与えられるグラフは以下のようなお姿をしています。
ここで重みが大きい程、エッジが太くなるように表現しています。さて、今度はグラフLaplace行列を計算して、その固有値と固有ベクトルを求めましょう。
import numpy as np
D = np.diag(W.sum(axis=1))
# グラフLaplacianを計算
L = D - W
# 対角化
Lambda, U = np.linalg.eigh(L)
# 固有値・固有ベクトルの並び替え
rank = np.argsort(Lambda)[::-1]
Lambda = Lambda[rank]
U = U[:,rank]
これだけで求まります。例えば3番めに大きな固有値に対しては、固有値と固有ベクトル(グラフ上の信号)は
> a = 2
> Lambda[a]
10.055243007102138
> U[:,a]
array([-0.48015202, 0.53358885, -0.08955028, 0.36487368, 0.1620922 ,
-0.14853339, 0.22086428, -0.11680288, -0.38401502, 0.17303859,
-0.235404 ])
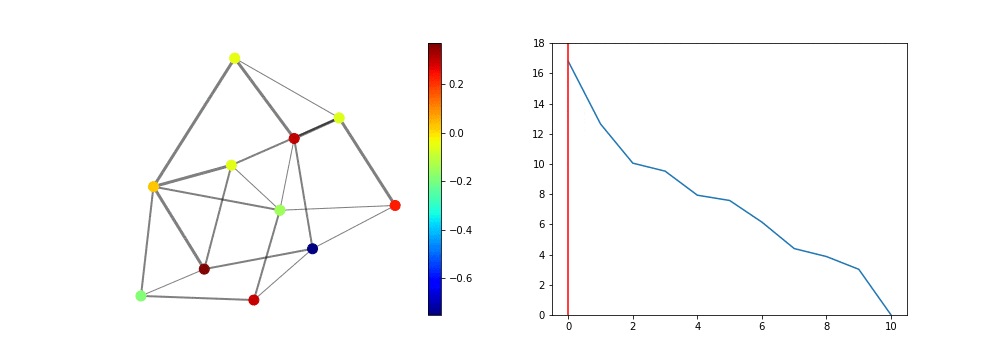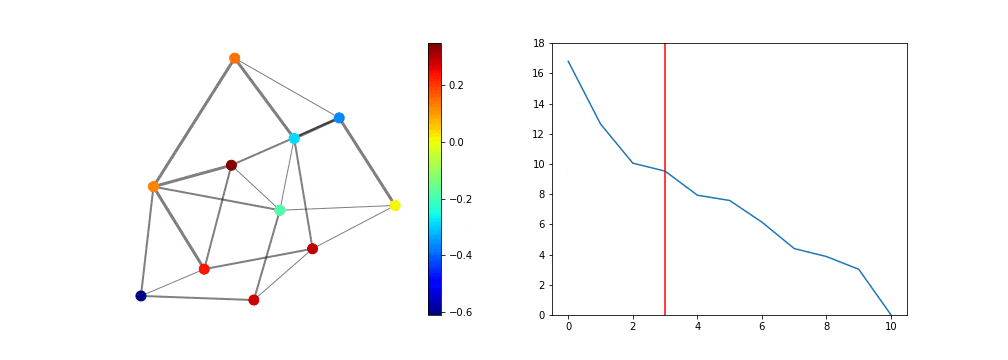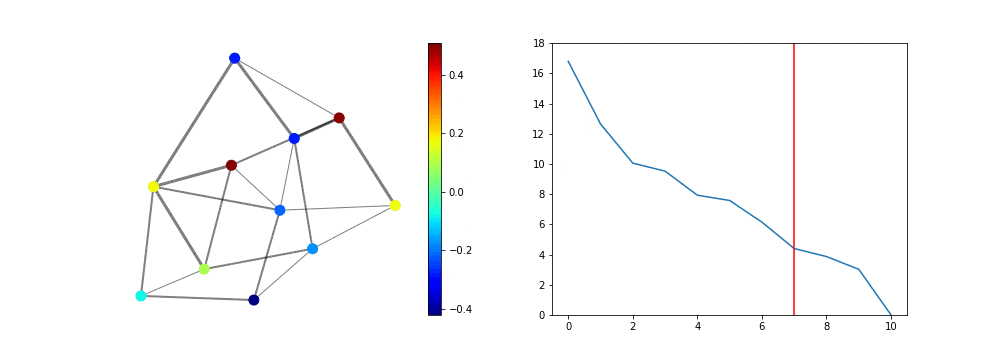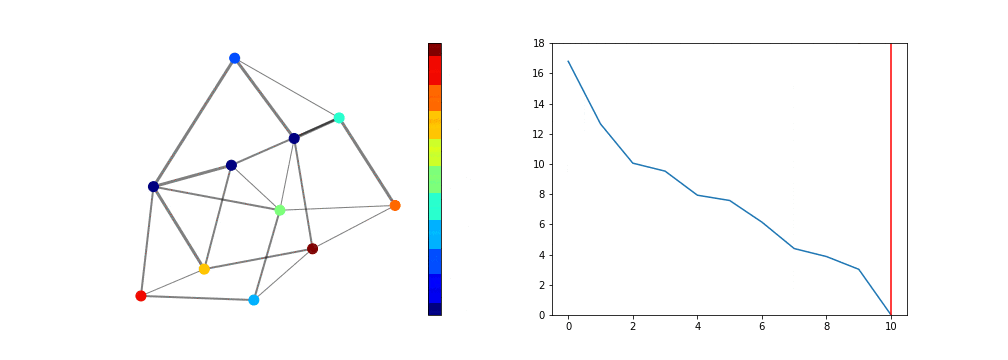
となります。さて、これをアニメーションにした結果が次です。7
ここで左図がグラフとその上の信号、右図が固有値をプロットしたもので、鉛直方向の赤線が今見ている固有値と固有ベクトルを表します。ここで注意して欲しいのが、固有ベクトルは$0$でない定数倍の自由度が存在し、これは実数に限定し、規格化を決めても、$(-1)$倍だけの自由度が残っています。つまり、今求めたグラフの信号を$(-1)$倍した信号を既定に用いても、何ら問題ありません。
さて最後に、固有値の大きさ(の順番)が何を意味するか、定性的な理解をしておきましょう。先の信号の符号だけを見てみます。
ここで固有値が大きいほど、隣接するノード間の符号が逆になる傾向にある事が見てとれます。これは、連続空間で固有値が大きい程、周波数が大きくなって信号が激しく振動する、という描像のグラフ版そのものと言えるでしょう。これは物理学、特に量子力学・物性物理学ではよく知られた話です。
言い方を変えると、グラフLaplace作用素の固有値は、グラフのスケール(の逆数)を表していると考えられます。すなわち連続空間で言うところの激しい振動数を持つ、あるいは周波数の大きな信号は、グラフの世界では、固有値の大きな固有ベクトルを成分に持つグラフ上の信号に置き変わります。
グラフ畳み込み
さて、いよいよグラフ畳み込みを定義します。
Gaussフィルターによる畳み込みの議論より、信号の振動が激しい程、畳み込みによる減衰も大きい、事が分かっています。特に減衰因子は、指数関数$e^{-ck^2}$($c$は適当な定数)で表せていました。
なのでグラフ上でも
\begin{align}
f_{\rm out} = U \; e^{-t\Lambda}U^T \;f_{\rm in}
\end{align}
のように定義するのは自然だと思われます。実際、これはGaussフィルターによる畳込みのグラフ版と言って差し支えないと思います。
しかし、今更ではありますが、フィルターは何もGaussフィルターだけではありません。世の中は無限のフィルターで溢れかえっているわけです。Gaussフィルターは理論上重要ですが、だらだらと未練たらしく尾を引いているので(これでも減衰は速い方なのですけどね)、応用上はあまり好ましくありません。そのためには、スペクトル空間で$e^{-t\Lambda}$をかける、という操作を、一般の$\Lambda$の関数$g(\Lambda)$に置き換えれば良いでしょう。
実際、以前述べた畳み込み定理を一般のフィルター$h(x)$に対して適用すると、畳み込みは、スペクトル空間上で$h(x)$をFourier変換した関数$\hat{h}(k)$の掛け算と等価である事が示せます。
よって、グラフの畳み込みも、一般の関数$g(\lambda)$(ただしTaylor展開可能な解析関数とする)に対して、
\begin{align}
f^{g}_{\rm out} = U g(\Lambda) U^T \;f_{\rm in}
\end{align}
と定義すれば良い事が分かります。ちなみに、もしGaussフィルターのように、固有値が大きいほど、減衰すべし、という条件を課す場合(low^passフィルター)、$\lambda \nearrow \infty$の時、$|g(\lambda)| \searrow 0$を要求する必要があります。
これで理論的には定義できたわけですが、応用上、厄介な点があります。それは、グラフFourier変換を実行するために、グラフLaplace行列を対角化しなければならない、という点です。
もちろん、グラフのサイズが小さければ問題ありませんが、大きくなるにつれて、ここの計算コストは行列サイズの3乗で増えるため、巨大なグラフには使えません。しかし、実はGaussフィルターに対して、Laplace作用素だけで畳み込みを表現できたように、一般のグラフ畳み込みを、スペクトル空間を経由せずに定義する事が可能です。8
鍵となる式は以下です:
\begin{align}
U g(\Lambda) U^T = g(L).
\end{align}
これは$g$がtaylor展開可能であることと、$L^n = U \Lambda^n U^T$を用いればすぐ証明できます。よって、グラフ畳み込みは$U$を使わずに
\begin{align}
f^{g}_{\rm out} = g(L) f_{\rm in}
\end{align}
だけで計算できてしまう事が分かりました。
多項式近似
一応、前節で定義が出来たのですが、一般の関数を取り扱うのはやや面倒です。そのため$g(\lambda)$を多項式のような簡単な式で近似してしまうのが、望ましいでしょう。しかし、(0以上の)実数上で定義される任意の関数を、多項式で近似するのは難しいと思われます。
例えば、グラフ版Guassフィルターの場合、$\lambda$が大きくなるにつれ、指数的に減衰します。
しかし$g(\lambda)=e^{-t\lambda}$を$K$次の多項式
\tilde{g}_K(\lambda) = \sum_{p=0}^{K} a_p \lambda^p
で近似しようとすると、$\lambda \nearrow \infty$ではその最大次数$a_K \lambda^K$が他の低次の項$a_{K-1}\lambda^{K-1}+\cdots$に比べて大きくなり、発散してしまいます。つまり多項式近似というのは、無限に拡がった空間上の関数を近似する道具としては適していません。
しかしある決められた区間内では、幾らでも近似可能である事が知られています。(Stone-Weierstrassの多項式近似定理)9
なのでグラフLaplace作用素の固有値に上限があれば良さそうですが、もうお分かりですね。正規化されたlaplace作用素を使えば良いわけです。これで、$[0,2]$区間上の関数$g$を多項式$\tilde{g}_K$で置き換える事ができます。
多項式の次数と畳み込みの近傍度合い
グラフ上のWaveletとChebysheff多項式による近似
時間があれば追記します。
グラフ粗視化とクラスタリング
啓示を受けたら加筆します。
まとめ
以上、グラフ畳み込みニューラルネットワークの構成するのに必要なパーツを見ていきました。
-
$:=$は左辺を右辺で定義する、という記号です。 ↩
-
ここら辺の用語は、分野や文脈によって変わると思うので、あまり詳細は気にしない事にします。 ↩
-
Laplace変換やMellin変換と言った、より一般的な積分変換についても成り立ちます。数学的には、局所コンパクト群のHaar測度による群上の積分と、Unitary作用素の積の関係にまで一般化されます。これは最近、球面上(等質空間)の畳み込みニューラルネットワークなどを定義する上で重要です。 ↩
-
よく用いられる定義と$(-1)$倍だけ異なります。これは$e^{ikx}$で張られる関数空間に対し、常に非負の固有値を持つようにするためです。 ↩
-
一般的な問題としては、こちらのほうが自然であり、むしろ連続的な空間にどうやって埋め込むか、が問題になります。その際に、先の熱核に基づく議論を進めると、多様体上のLaplace-Beltrami作用素は、グラフLaplace作用素の連続極限で得られる事が知られています。また重み$w$と距離$a$の関係は、$w \sim \exp(-a^2)$で与えられます。 ↩
-
ちょっとcolorbarの範囲設定に手間取りそうだったので、毎回軸の範囲が変わっています。余裕がある時に修正しますが、もし方法が分かる方いらっしゃいましたら、ご教授ください。 ↩
-
Gaussフィルター以外のフィルターでも、$x$の偶関数であれば、通常のLaplacianで表現可能です。 ↩
-
これはニューラルネットワークの万能近似定理でも同様ですね。 ↩