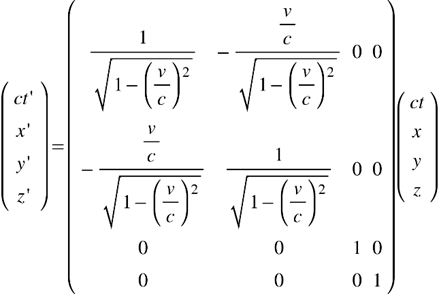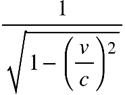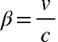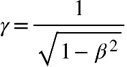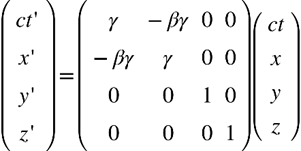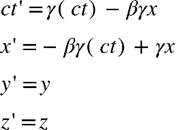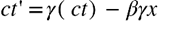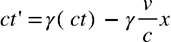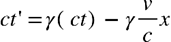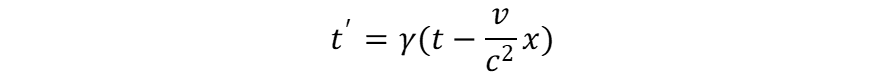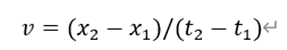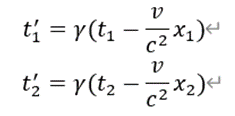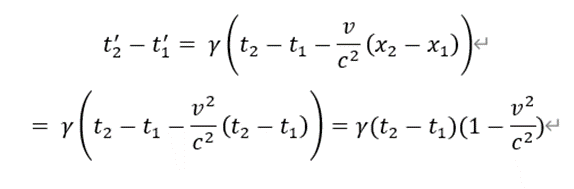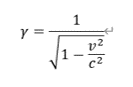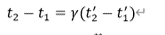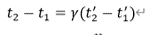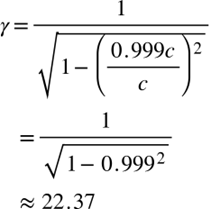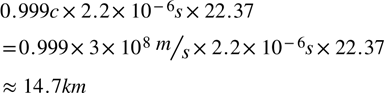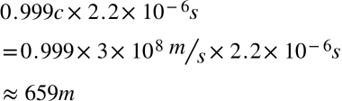★前回投稿した記事の内容を一部変更しています。
(時間の遅れについてより正確に記述しました)
はじめに
相対性理論と聞くと、様々な不思議な現象を思い浮かべるかもしれません。
厳密な表現ではありませんが、例えば、「運動している物体は時間がゆっくり流れる(特殊相対性理論による効果)」とか「地上から離れている物体は時間が早く流れる(一般相対性理論による効果)」といったものです。
他にも同じような効果で、「物体を加速すればするほど重くなる(質量が増える)」、「ブラックホールに近づけば近づくほど時間がゆっくり流れる」なども聞いたことがあるかもしれません。
こうした不思議な現象については、いろいろな入門本に書かれており、私もよく読んだ記憶があるのですが、どうも信じられないような気もしていました。
そこで今回は、相対性理論の数式を使ってみて、確かにそうした現象を数値として計算できれば面白いなあと思い、「運動している物体は時間がゆっくり流れる(特殊相対性理論による効果)」を記事にしてみました。
μ粒子の不思議な現象
先程の「運動している物体は時間がゆっくり流れる(特殊相対性理論による効果)」という表現ですが、この現象をもう少し厳密に言うと、「等速直線運動をしている物体」の速さが大きくなればなるほど、「静止している人」から見ると、その「移動体の刻む時間がより遅く観測される」ということです。これは、静止している人から見るとその「移動体の寿命が延びる」ということにもなります。
この効果が実際に観測されている例として、μ粒子について見ていきたいと思います。
★ μ粒子とは
μ粒子は電子の仲間の素粒子で、英語ではミューオンと呼ばれています。μ粒子は加速器で作ることもできますが、自然界(地球の大気の上層部)でも発生しており、実際に観測することができます。
このμ粒子は、大気上層部(例えば約10Kmの上空)で、宇宙(超新星残骸など)からやってきた高エネルギーの宇宙線(主に加速された陽子)と大気中の原子(窒素や酸素の原子核)との衝突により発生します。そして、発生後わずかに平均 2.2μS (2.2×10のマイナス6乗秒)で他の粒子に崩壊します。μ粒子は崩壊する前に地表で観測されています。つまり、2.2μ秒の間で約10Km飛ぶことになります。
★ μ粒子は地表に到達できるのか
こんな短い時間で10Kmも飛ぶのかなぁと疑問を持つ方もいらっしゃるかもしれません。そもそも、μ粒子は2.2μSの寿命で地表まで到達することができるのでしょうか。
μ粒子が発生するのは約10Kmの上空で、そこから仮に光速で地表に向かったとしても、2.2μSでは約660mくらいしか飛べません。μ粒子の速度は平均で光速の概ね99.5%ですから、これでは到底地表に到達することはできません。
ところが、実際には地表でμ粒子が観測されているのです!! (下図参照)
これは一体どういうことなのでしょうか?
出典:「東京大学宇宙線研究チームの解説図」を元に作図
μ粒子の寿命が延びる!?
実際に地表でμ粒子が観測されるということは、「飛んでいる時間が延びた」ということです。これはつまりμ粒子の寿命が延びたということです。
「寿命が延びる」なんてことはあるのでしょうか。
★ カギは特殊相対性理論だ
この謎のカギを握るのが「特殊相対性理論」です。
この理論によると、「等速直線運動をしている物体(例えばμ粒子)の時間は、静止している系(例えば地上の観測装置)から見るとゆっくりと進む」というものです。この効果は数式で計算することができます。
では、実際に特殊相対性理論の式を使ってμ粒子の寿命がどれくらい伸びるのかを計算してみましょう!
「時間の遅れ」を特殊相対性理論で計算だ!
★ 準備体操
特殊相対性理論には、2つの慣性系(例えば、物体が運動している系と静止している系)との間の関係を示す変換式が存在します。ここで、慣性系とは、静止している系(座標系)か等速直線運動している系(座標系)のことです。
この変換式を使っていろいろと計算すると、2つの慣性系の間には時間や空間が相対的に異なって見えることが分かります。
例えば、高速で移動する系を静止している系から見ると、その移動している系の時間が遅くなったり、移動する方向の空間が縮んで見えたりします。その逆、つまり自分が高速で移動していると、向かってくる相手の系の時間が遅くなったり自分の進行方向の空間が縮んで見えたりします。不思議ですね!
また、相対性理論では、3次元の空間と時間を合わせた4つの次元を扱いますので、この2つの系の関係を示す関係式にも4つの次元が使われます。具体的には、空間の3次元(例えば、x,y,z)と時間(ct)です。ct の c は光速で、t は時間です。x,y,zが長さの単位を持っているため、時間も長さの単位にするために ct (速度×時間で距離つまり長さ)としています。
ややこしい話はさておき、下記は、この変換を表す式で、ローレンツ変換と呼ばれています。
(ただし、x軸方向に速度vで進む場合。今回は式の導出は割愛します)
この変換式は行列の形で表現されており、右辺の慣性系S(ct,x,y,z)(ここでは静止している慣性系)が、その左横の4×4の座標変換行列によって、左辺の慣性系S'(ct',x',y',z')(ここではμ粒子のような等速直線運動をしている慣性系)に変換されています。ただし、等速直線運動の向きははx軸方向とします。なので、上記の式は、「x軸方向のローレンツ変換」となります。
尚、座標変換行列の c は光速で、vは等速直線運動をしている物体の速さ(厳密には、S'がSに対して+x方向に速度vで動いている)です。
尚、この記事では触れませんが、実はこの式をよく見ると、物体が光速を超えられない理由が見えてきます。
この式の中で実際にμ粒子の寿命の計算に使うのは、ct の部分です。なぜなら、ct に時間 t が含まれているからです。
では、寿命の計算に使えるようにするため、この行列の ct の部分を展開しておきます。
おっとその前に、上記の式だとあまりにも煩雑なので、座標変換行列を簡略化します。
ここで、座標変換行列の
となります。だいぶスッキリしました。
そして、行列を展開すると、
が得られます。
この中で、時間に関係する下の式を使います。
そして、後で計算しやすいように、先程のβを v/c に戻して、下記のように変形して、
とします。
★では、本番!
これで準備が整いました。
では、行きます!
まず、2つの慣性系のうち、地上系をS系とします。地上の観測装置は静止しているので、静止系でもあります。ローレンツ変換式の右辺の慣性系S(ct,x,y,z)が地上系です。
そして、μ粒子をS'系とします。μ粒子は運動しているので、運動系です。同じく、ローレンツ変換式の左辺の慣性系S'(ct',x',y',z')に相当します。
つまり、
の式で、左辺の t' がμ粒子の時間で、右辺の t が地上での時間です。この2つの時間の関係を調べます。
後で計算しやすいように、上の式を少し変形します。
両辺をCで割ってγでくくります。
ここで、それぞれの時間の流れ(変化)を、
のように最初の時間から次の時間に経過するとします。(経過を→で示しています)
さて、今、2つの異なる慣性系の間に時間の流れの違いがあるかどうかを調べようとしています。
2つの慣性系の間の時間の関係について調べるには、運動する物体(この場合ミュー粒子)を慣性系S(静止系)で測定します。
このとき注意が必要なのは、慣性系S’は運動しているミュー粒子にへばりついて移動しているということです。つまり、慣性系S’から見るとミュー粒子は止まっているということです。慣性系Sから見るとミュー粒子は運動しています。
ここで、運動しているミュー粒子を時計に置き換えて考えてみます。この時計は一定の間隔で時を刻んでいます。この時を刻む間隔が2つの慣性系で異なって見えることを、これから計算してみます。
今、慣性系Sからみて速度vで運動している時計を慣性系Sで測定します。
最初に、時計が静止している(時刻は刻んでいます)慣性系S’において時間がt1'からt2'まで経過したとします。
このとき、慣性系Sで時計を測定すると、時間はt1からt2と経過し、時計も動いているので、その位置をx1からx2まで移動したと観測します。
時計は、速度vで移動しているので、
すると、2つの慣性系の時間の関係は下記のようになります。
1番目の式が、両方の慣性系での最初の時間と慣性系Sで測定した位置を表し、2番目の式が次の時間と位置を表しています。vは慣性系Sで測定した時計の速度です。
そして、先程の速度vの式を使って、この2つの時間の差をとると、
となり、この式に
を注意深く組み込んで計算すると、下記が得られます。
この式の意味するところは、運動系での時間の間隔(刻むスケール)のγ倍が静止系の時間の間隔になるということです。
例えば、γが10とすると、運動系の1秒は静止系の10秒となります。つまり、運動系の時計が1秒しか経っていないのに、地上の静止系の時計は10秒も経過していることになります。逆に言うと、地上で1秒経っても運動系では0.1秒しか経っていません。
運動系の時計のスケール(時間の刻み)が小さくなっているように見えます。
ということは、地上からみると運動系の時間が1/10にゆっくり流れている、つまり10倍に寿命が延びているように見えるわけです!
★ μ粒子の寿命は、静止している時と運動している時とでは大幅に異なる!
実は、μ粒子の平均寿命は 2.2μ 秒とありましたが、これは、静止系での寿命です。つまり、μ粒子が静止している時の寿命です。
実際に10Kmの上空で生まれるμ粒子は、もの凄い速さで運動しています。例えば、光の速さの99.9%の速さです。つまり、μ粒子は運動系の世界にいるので、地上(静止系)から見るとμ粒子の寿命は延びているように見えます。
★ 寿命が何倍延びるか計算しよう
では、実際に計算します。
使う式は、非常にシンプルな形になります。要は、γを求めればいいわけです。
におけるγですが、改めてγは、
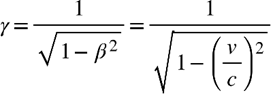
でした。
ここで、μ粒子の速度を光速 c の99.9%とします。上の式のvはμ粒子の速度で、v=0.999c となるので、
となります。
つまり、μ粒子の寿命は地上からみると、約22.37倍に伸びることになります。
★ では、寿命が延びるとどれくらい移動できるのか?
2.2μ秒の寿命が約22.37倍に伸びると、0.999cの速度で運動するμ粒子の移動距離は、光速cを秒速30万Kmとして、
となり、14.7Kmも飛ぶので、地上の測定装置まで届くことになります。(μ粒子が発生したのは上空10Kmとしています)
もし、寿命が2.2μ秒なら、
となり、わずか約659mしか飛べません。
ということで、特殊相対性理論の効果によるμ粒子の飛行距離を計算することができました!
如何でしたでしょうか。
さて、この記事もおわりに近づいています。
最後に、μ粒子から見た地上(地球)の動きをみてみましょう。これは、μ粒子の気持ちになって考えてみると面白いかもしれません。
μ粒子から見ると、地上の時間が延びて大気が薄くなる?
これまでは、地上の人間(静止系)からみたμ粒子(運動系)の振る舞いでした。
でも、μ粒子はきっとこう言うでしょう。
「いや~、寿命が延びると言われても実際には平均で2.2μ秒しか生きれないし・・・ でも、ちゃんと地上の測定装置に飛び込んでるんだよね・・・」
うーん、どういうことでしょうか?
★ 相対性理論はお互い様
実は、これまで地上から見てきたμ粒子の振る舞いと同じことが、μ粒子から地上(地球)を見る時にも起こります。
つまり、μ粒子にとっても、地上の時間が約22.37倍に伸びるように見えます。
もう少し正確に言うと、慣性系S'(μ粒子自身)から見れば、慣性系S(地球)が自分に向かって光速の99.9%のスピードで動いているので、先程の計算で立場が入れ替わり、地球の時間が22.3倍に伸びることになります。
実は、これに加えてもう一つ特殊相対性理論の効果が出てきます。それは、「μ粒子から見ると地球が 1/22.37 に縮んで見える」というものです。
言い換えると、μ粒子にとって大気の厚さが 1/22.37 に薄くなるのと同じことになります。先程の計算で、地上から見ればμ粒子は約 14.7Km 飛んでますが、μ粒子から見れば、この効果によって14.7Km の距離は 1/22.37 の 659m になります。だからこそ、自分の本来の寿命である2.2μ秒の間に地上に届くことになるわけです。
なので、μ粒子はこう言うかもしれません。
「地上の人間は「μ粒子の寿命が延びている!」と騒いでるけど、大気が縮んで見える方が驚きだけどね・・・」
★ まとめ
以上まとめると、地上から見たμ粒子の時間はγ倍伸びて、μ粒子から見ると大気層(地球)は1/γ に縮むことになります。
ちなみに、この縮むことを「ローレンツ収縮」と言います。このローレンツ収縮は、先程のローレンツ変換の式から導出できます。
ということで、長い話になりましたが、特殊相対性理論の効果によってμ粒子が地球に届く様子をみてきました。同時にμ粒子にとって地球がどのように見えるか、つまりμ粒子の気持ちも推し量ってみました。
おわりに - まだまだ続く相対性理論の議論 -
今回の記事はこれで終わりですが、相対性理論は大変奥深く、様々な研究が続けられています。アインシュタインによる発表から100年が過ぎ、なおも尽きない謎が広がっています。
ブラックホールの物理や重力波による宇宙の観測、重力場と量子場の統一(量子重力理論)など長い道のりが待っています。
私自身、まだまだ始めたばかりの初心者ですので、これからも一歩一歩 相対論を精進していきたいと思っています。
最後まで読んでいただき、ありがとうございました。
参考文献
講談社基礎物理学シリーズ 相対性理論 杉山 直 著
ベル出版 一般相対性理論を一歩一歩数式で理解する 石井 俊全 著
理工図書 趣味で相対論 広江 克彦 著
講談社 アインシュタイン方程式を読んだら「宇宙」が見えた 深川 峻太郎 著
名古屋大学理学研究科・素粒子宇宙物理系F研
https://flab.phys.nagoya-u.ac.jp/2011/appli/muon/
東京大学宇宙線研究チーム
https://www.icrr.u-tokyo.ac.jp/prwps/common/muon/page4.html
★ ちなみに、相対論を広く浅く手短に一通り学習したい方は、上記の「アインシュタイン方程式を読んだら「宇宙」が見えた」がおすすめです。
この本で全体を俯瞰すれば、他の本にスムーズに学習を進める事が出来ます。