(complex) morlet waveletの係数の名前の付け方とか、ほどよい設定値とか資料によって異なっているので、可能な範囲で整理してみた

あまり整理できてませんが・・・

1. waveletの式の変数とか式が少しずつ違ってて,きちんと同じものを指しているかよくわからない.

ref. matlabの資料が参照している(と思われる)Teolis(1998)Computational Signal Proceesing with Wavelets. P66より

式

変数の名前

γb: variance (bandwidth)と命名してある. matlabの資料のfbと同じ.時間的分散と思われる.しかしここでの時間的分散とは何?
γc: center frequencyと命名してある. これはほとんどどれでも一致している. mneとかでfrequencies = np.arange(8,30)とかで設定する値と理解してます.
j: 虚数単位

ref. stack overflow

式

w(t,f₀ ) = A・exp(−t² / 2*σ² )・exp(2*i*π*f₀*t) = A・exp(2 iπ f₀ t - (t² / 2σ²))

変数

f₀: center frequency (上のγc、matlab wavelet toolboxではfc)
σ: σ = m/2πf₀ と記載されている. Tallon-Baudry (1999)の記載にあるように時間に関する標準偏差(sigma t)の意味ぽい. 上のTeolis(1998)の式と比較して、
γb = 2σ²　と仮定すると一致する.
m: 定数. compromise between time and frequency resolutionとある. 7に設定しました、とも.
A = 1 /(σ (2π)^0.5) = 1/(σ√2π): e(exp)の前の部分を変数に置き換えてある. normalization factorという名前で紹介している.

ref. Tallon-Baudry (1999), p154 Box 2の説明

式

w ( t , f ) = A . e x p ( – t²/ 2σ_t² ).exp(2i π f t): これはstack overflowと同じ.

変数

f: 上のf₀と同じ. center frequency
σ_t: 上のσと同じ. time domainの標準偏差と記載あり.

A=1/(σt √π)1/2: stack overflowと同じくnormalization factorと書いてある. 式がちょっと違う. Tallon-Baudry(1997)でも同じ記載をしている.意図があるのか,間違え+コピペなのか不明.

ref. matlab wavelet toolbox

式

ψ(x)=1/√πfb * exp(x² / fb) * exp(2iπfcx) :コピペがうまくいかなかったので、書き写し.
上の2つと比較してexp(x²/fb)の部分にマイナスがついていない. このページだけなので、間違えのような気がします.
他はTeolis(1998)、stack overflowと一致

変数

x: 上のtと同じ
fc: 上のf0とかf、γcと同じ. center frequency
fb: bandwidth parameterと名前が付けられている. Teolis(1998)のγbと同じ.

ref. matlab help

式

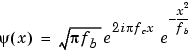
またちょっと違う. eの前 (上に出てくるA: normalization factor)の部分で分母と分子が逆になっている.分母分子の違いはこのページだけなので、たぶん間違い.
他はTeolis(1998)、stack overflowと一致

変数

fc, fbの名前の付け方はmatlab wavelet toolboxと同じ

ref. Stack exchange wavelet cmor fb fcとかググると上位でヒットします.

式

e^-j2pifctのマイナスは不要と思われる.

1のまとめ

総合判断すると(complex)Morlet waveltの式はTeolis(1998)Computational Signal Proceesing with Wavelets. P66、Stack overflowの記載が正しいような気がします. Teolis(1998)はテキストだし.
てか資料によってほんとに式が微妙に違ってて, 実は間違いだらけなのかという気がします.

2. waveletのほどよい設定とは.(主にmne pythonを念頭に)

fieldtrip(time-frequency analysis, waveletの項)

cfg.width. It determines the width of the wavelets in number of cycles. とあります. サンプル中では

cfg.width = 7;

となっていました.
また,
The spectral bandwidth at a given frequency F is equal to F/width*2
the wavelet duration is equal to width/F/pi
と記載があります. Fは周波数で、上記のcenter frequency (f, f₀,γc, fc)と同じものと思われます.

• ただspectral bandwidth, wavelet durationが何を指しているかよくわかりません.
• spectral bandwidthがσ_fとか,wavelet durationがσ_tに一致するとか, そんな簡単な関係ではないようです. 用語が多くて混乱します.

Tallon-Baudry(1999)

σ_f = 1/(2πσ_t) (式2.1)
と関係を示してあります.

• σ_t はstandard deviation (time domain)と記載されています. 今まで何度か出てきたσ_t, σと同じもののようです.
• σ_fは同様にstandard deviation (frequency domain)と記載されています。

f/σ_f (constant ratio: greater than five in practice) (式2.2) と記載されています.

• fはcenter frequency(fieldtripの記載のF, 上の方出てくるf₀,γc, fc)と同じと考えてよいようです.

Roach & Mathalon (2008)

σ_t = 1/(2πσ_f) (式2.3)
と関係を示してあります.Tallon-Baudry(1999)の式(2.1)を変形すれば同じになります.

変数の記載

σ_t: temporal SDと記載されています.
σ_f: spectral bandwidth around its center frequency, f0, that has a SD of σ_fとあるので周波数のSDと言えそうです.Morlet waveletはgaussian envelope(正規分布のエンベロープ)という言葉がちょいちょい出てくるのでSDがwaveletの形の指標として使いやすいのでしょう.
ただ、同じページの下の方に
spectral bandwidth around any given center frequency is mσ_f.
ともあります。mが掛けられています。これらから察するに
spectral bandwith = mσ_f , and has σ_f in it.
という意味なのかと想像しています. 本文が混乱させる記述で困ります.

c=f₀/σ_f (式2.4)
とc (constant ratio)という変数を定義してあります(たぶんcfg.widthと同じモノ). これも式2.2に変数cが割り当てられただけで、同じものを指していると考えられます.

• cは5,6,7くらいの数字がよいと本文中で推奨されています. 理由はσ_tが1周期以上の波を含むように,だそうです ("constan, c, is typically recommended to be greater than 5, and is often set to values of 6 or 7, which corresponds to a σ_t that encompasses at least one full sinusoidal cycle for any particular frequency").-
• stack overflow中にσ = m/(2 π f₀) という式が出てきて(σ = σ_tと思われる)、下の式(2.5)と一致します.なのでこの式のmとconstant ratio cは同じものを指していると思われます.

ちょっと余談: cが7くらいだとσ_tが1周期以上の波を含む、の説明 (間違ってるかもしれません)

---

式(2.3), (2.4)を用いてσ_t =の形に変形をすると

σ_t = c/(2πf) = c/(2π)*1/f (式2.5)という式が得られます.

• fは周波数なので1/fは1周期分の時間ということになります.
• ということで1/fの前にあるc/(2π)が1を超えると, σ_tが1周期以上の波を含むように, という (なぜそのような長さが必要か理由はわかりませんが)推奨を満たすことができます.
• 2π = 6.28ちょっとなのでc=7でc/(2π) > 1となり, σ_tが1周期を超える波を含む,と考えられます.

よくわからない変数m

Roach & Mathalon (2008)にa factor mとして説明があり,
temporal window for any given frequency (f₀) is m σ_t (式2.6)
とあります. temporal windowが何を指しているかよくわかりません.
ただ, temporal windowはfieldtripに出てくるwavelet durationと同じものではないか?という気がします. 式を変形してみましょう.

式(2.6)と(2.5)から
temporal window = mc/(2π)*1/f = mc/(2π)/f となります.
上のfieldtripの箇所に記載を繰り返しますが,

wavelet duration is equal to width/F/pi (式2.7)
F=f なので,c=widthと仮定し, m=2とすると, temporal window = wavelet duration
が成り立ちます.
temporal window (by Roach & Mathalon(2008)) = wavelet duration (by fieldtrip)としてよさそうです.

Roach & Mathalon (2008)中には
spectral bandwidth around any given center frequency is mσ_f
という記載もあります. これもfieldtripのspectral bandwidthと同じでしょうか.
fieldtripより: spectral bandwidth = F/width *2

先のwidth = cが正しいとすると, c = f₀/σ_f (式2.4)
とありますので.

Roach & Mathalon(2008)のspectral bandwidth = mσ_f = mf₀/c = F/width * m (fieldtripの式)
ということで,やはりm=2で同じものを指していると言えそうです.

またfieldtripのcfg.width = c (constant ratio)と言えそうです.

用語が多すぎです. 混乱します.
ちなみにfieldtrip中ではこの"m"に相当する明示的な記載はありません.内部で適当に処理してるのでしょうか.

• Roach & Mathalon (2008)のreferenceですが, Tallon-Baudry (1997)の方に, "wavelet duration 2σ_t of about two periods of oscillatory activity at f₀" と記載が出てきます. ここでもm=2として扱ってるようです.
• Ford et al (2008)では"constant ratio (σf=f/7) and wavelet duration (4σ_t)""spectral bandwith of 4σ_fと記載があります. fieldtripでのcfg.width =7 (他の資料ではconstant ratio)で, Roach & Mathalon (2008)のm=4の設定のようです.
• "mは6推奨だけど,4とか2の解析例もある" と記載しています(Roach & Mathalon (2008)).

MNE python

• tfr_morletとかで周波数分析できるが、n_cyclesというそれっぽい設定項目があります.
• ただ"The number of cycles globally or for each frequency."という記載でn_cyclesがcを指してるか,temporal durationを指してるか, mを指してるかさっぱりわかりません.
• 解析例を見ると7とか2とかfreq/2とかfreq/3とか見かけました.
• というわけで結局よくわかりません.設定例に7とかあるので, fieldtripのcfg.widthと同じじゃないかなーとか,その程度です.

参考：tfr_morletが内部で使っているmorletのスクリプトを覗いてみると

mne/time_frequency/tfr.pyにdef morletがあります.スクリプト中に
tfr.py
sigma_t = this_n_cycles / (2.0 * np.pi * f)

とあるので, 式(2.5)からするとthis_n_cycles (=n_cycles) = c (constant ratio)でないかと思います.

2のまとめ

• fieldtripのcfg.widthとmne pythonのn_cycles, 資料に出てくるc (constant ratio.式2.4), stack overflowのmは同じものを指しているぽい.パラメータの意義を理解"できませんが", constant ratioのところを読んで少しでもわかるように努めたいと思います. なおRoach & Mathalon (2008)のmはまた別.
• σ_tはtemporal SDであり、wavelet duration (おそらく=temporal window)とは異なる. wavelet duration = mσ_t (Roach & Mathalon (2008)より)
• 同様にσ_fはfrequency SDでありspectral bandwidthとは異なる. spectral bandwidth = mσ_f (Roach & Mathalon (2008)より)
• constant ratioの説明も含め7に設定してるのをよく見かけるので,cfg.widthとかn_cyclesの設定はまず7で見るのがよいであろう.
• Roach & Mathalon (2008)のmはmne python, fieldtripでは明示的に設定するところはない(と思う). fieldtripはm=2ぽい. mneも同等ではないか.
• mne pythonでn_cycles = 2とかの解析例あり(source_band_induced_powerの例なのでwaveletとは違うかもしれないが). 適切な設定なのかは未だ不明. Roach & Mathalon (2008)ではcは5以上と書いてあるので, このずれからすると n_cycles = cではない可能性も...
• そもそもMorletとcomplex morletの違いがちゃんと分かってません.なのでこれを当てにせず,資料を1つずつあたりましょう.