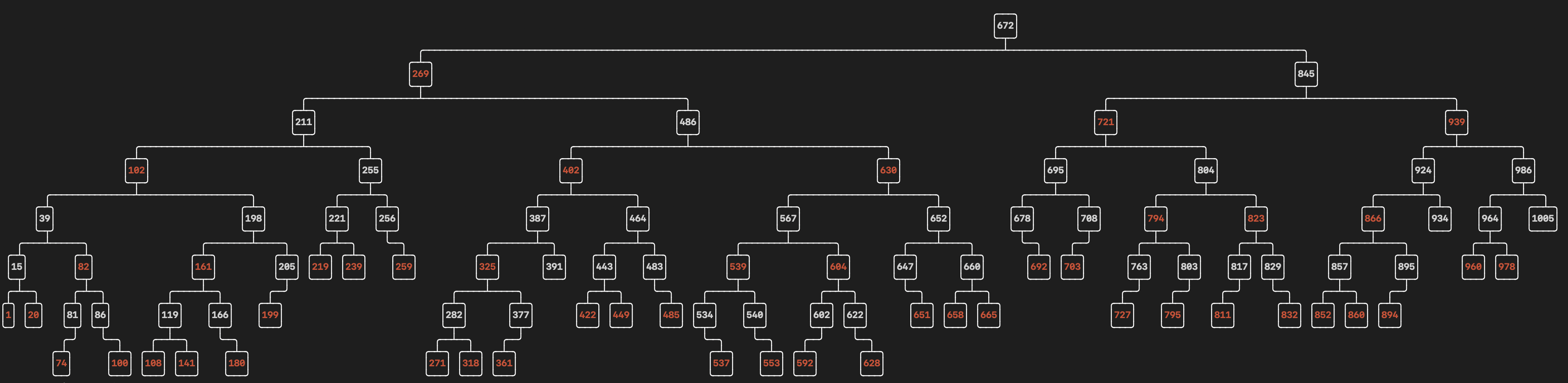
序
こんにちは、42tokyo Advent Calendar 2022 の18日目を担当する、在校生のyokawadaです。
42tokyoでは主にカチコミをしています。
皆様におかれましては、職場で、学校で、あるいはご家庭での「木を可視化したい!」との思いに日々お悩みのことと思います。
本記事が、そのような状況への一助となりましたら幸いです。
問題設定
一言でいうと「二分木の構造をAA(アスキーアート)で可視化する」。
たとえばこんな感じに:
(二分)木ってそもそも何よ
本題ではないので、ざっとだけ説明する。
- 木
- 「ノード(節点)」同士を「エッジ(辺)」で繋いだ、いわゆるグラフ構造のうち、閉路を持たないもの。
- この記事で扱う木は、エッジが向きを持つ(有向)ものとする。
- 親ノード・子ノード
- エッジがあるノードから出て別のノードに入るとき、エッジが出ている方を親、入っていく方を子と呼ぶことにする。
- 根ノード
- 子でない(親を持たない)ノード。
- 言い換えるとエッジが入ってこないノード。
- あっても1つしか存在しない。
- 二分木
- すべてのノードが2つ以下の子しか持たないような木のこと。
どんな木を描くか
まずは描きたいものを実際に手で作ってみる。

こんな感じだろうか。
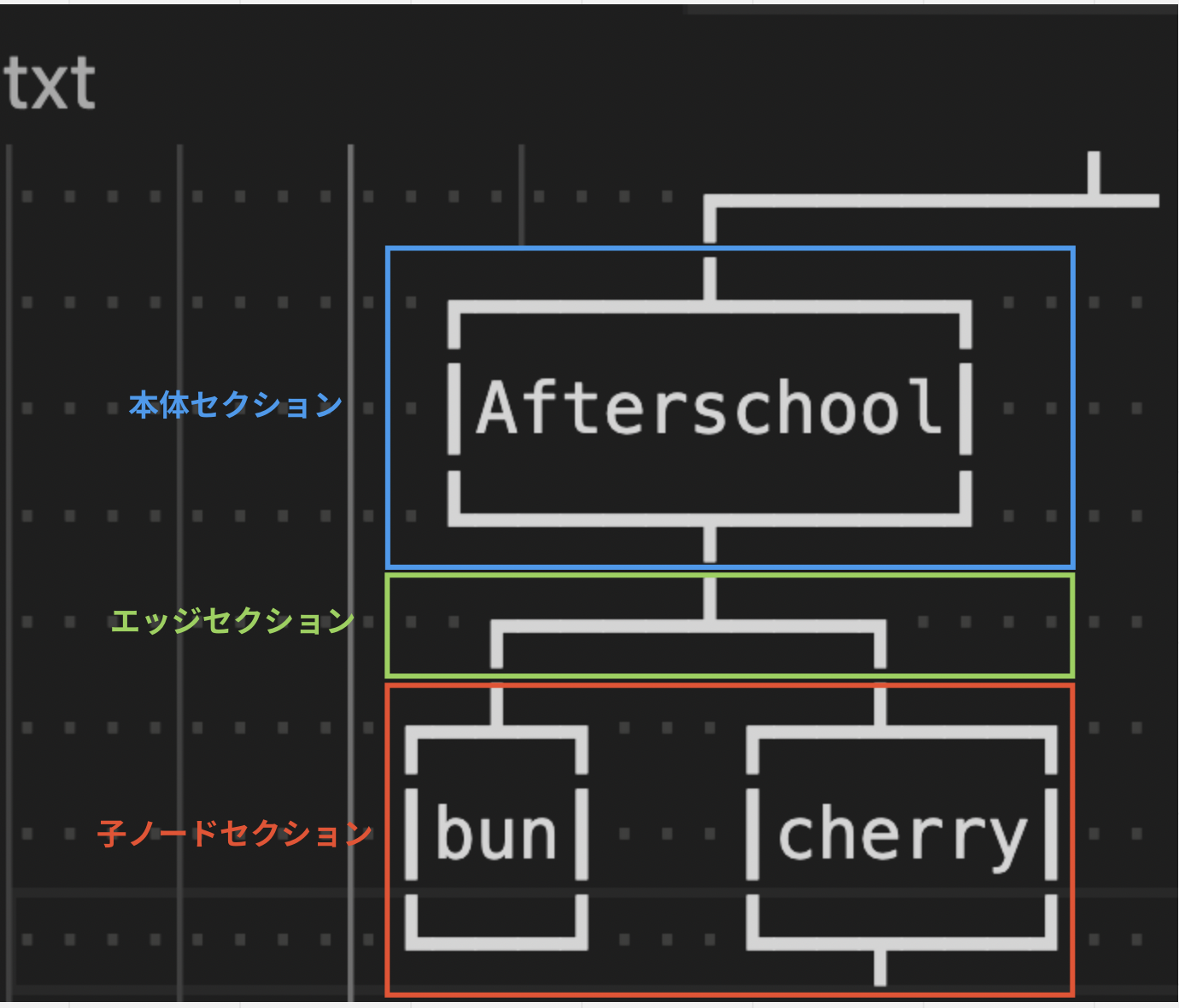
この木はおおまかには次のような構造を持っている:
-
本体セクション
- ノード本体を内包するセクション。
-
エッジセクション
- 本体と子ノードを結ぶエッジを有するセクション。
- 子ノードを持たない場合は存在しない。
-
子ノードセクション
- 左右の子ノードを内包するセクション。
- 縦にそれぞれ左・中央・右として三分割される。
- 左右もまたそれぞれ再帰的にセクションに分割される。
- もちろん子ノードを持たない場合は存在しない。
これら3セクションをちょうど内包する矩形領域をバウンディングボックスと呼ぶことにする。
それぞれのセクションをさらに細分する:

- 本体セクション
-
本体中央パート
- ノードの中央1文字分の領域。
- 親があれば親からのエッジが上辺に、子がいれば子へのエッジが下辺にそれぞれ結合している。
-
本体左パート・本体右パート
- 中央パートの左右にあるパート。
- ノード文字列の長さに応じて大きさ(幅)が変わる。
- 左右の大きさは均等だが、等しくできない場合は左の方を1文字多くする。
-
本体中央パート
- エッジセクション
-
ジャンクション
- 親側ノードから降りてきたエッジがビームと交わる部分
- サイズは1文字x1文字
-
ビーム
- ジャンクションから左右に分かれて子ノードに向かう部分
- 高さは1文字分
-
左コーナー・右コーナー
- ビームが曲がって子側ノードに降りていく部分
- サイズは1文字x1文字
-
ジャンクション
- 子ノードセクション
-
左子バウンディングボックス・右子バウンディングボックス
- 左右の子自身のバウンディングボックス
-
左子バウンディングボックス・右子バウンディングボックス
「レイアウトを決定する」とは、「画面上に描画されるものについて、その位置とサイズを1つに定めること」と捉えることができる。
上記の要素についてそのことを考えてみる。
各要素の位置とサイズ
(分量が多いので気合いで読んでください。ていうかコードを読んだ方がマシかもしれません。)
ある1つのノードに着目し、そのノードの各要素について位置とサイズが満たすべき条件を調べる。
以下、着目しているノードが持つ文字列の文字数をLと表記する。
まずはサイズから。
サイズ
-
本体中央パート
- 横幅
wcは1文字固定とする。 - 高さ
hcは、文字列表示に1文字, 上辺と下辺に1文字ずつ使うことにして、合計3文字分。
- 横幅
-
本体左パート・本体右パート
- 高さ
hl, hrは中央パートと同じ。 - 長さ
Lの文字列のうち1文字は中央パートに表示される。残りを左を右で分け合うが、均等にならない場合は(前述の通り)左を1文字多くするルールだった。 - よって、左パートの横幅は
wl = L / 2 + 1, 右パートの横幅はwr = L - 1 - L / 2 + 1 = L - L / 2と書けることになる。- ※除算は小数点以下を切り捨てる。
- 以下、
h = hc = hl = hrで本体セクションの高さを表すことにする。
- 高さ
-
ジャンクション
- 前述の通り、存在しているなら幅も高さも1文字とする。
-
左コーナー・右コーナー
- こちらも、存在しているなら幅も高さも1文字とする。
-
ビーム
- 高さは(存在しているなら)1文字とする。
- 横幅については後述する。
-
バウンディングボックス
- 左子バウンディングボックス、右子バウンディングボックスについては再帰的にサイズを決定する。
- バウンディングボックスのサイズは、左右の子のバウンディングボックスと本体左右パートの兼ね合いで決まる。
- 高さは、
H = [本体セクションの高さ] + [エッジセクションの高さ] + [子ノードセクションの高さ]となる。 - 本体セクションの高さは
hc = hl = hr = 3. - エッジセクションの高さは1または0.
- 子ノードセクションの高さは
max([左子ノードのH], [右子ノードのH])となる。- ※ただし, 子ノードが存在していない場合はバウンディングボックスのサイズは0とみなす。今後も同様。
- まとめると、
H = 3 + (1 or 0) + max([左子ノードのH], [右子ノードのH]). - 横幅
Wは、左・中央・右に分けて考える。 - 中央の幅は
Wc = 1. - 左の幅は
Wl = max(wl, [左子ノードのW]). - 右の幅は
Wr = max(wr, [右子ノードのW]). - 和をとって
W = Wl + Wc + Wr = max(wl, [左子ノードのW]) + 1 + max(wr, [右子ノードのW]). - お気持ちとしては「本体と子ノードのバウンディングボックスのうち、より大きい方を取る」となる。
-
ビームの横幅
-
Wl, Wrを定式化したので、ビームの横幅が計算できる。 - 左側のビームの横幅は
wbl = [左子ノードのWr] - 右側のビームの横幅は
wbr = [右子ノードのWl]
-
位置
考えるのは要素の左上の位置。
なお、同じセクションにある要素は、1つ位置が決まると他もすべて決まるので、
真面目に考えるべきものはそれほど多くない。
-
バウンディングボックス
- 縦位置
Yは、親ノードの直下からさらに1文字下がればよいだけなので、あまり難しくない。 -
Y = [親ノードのY] + [親ノードのh] + 1. - 横位置
Xは、ノード自身が左子か右子か(あるいは根ノードか)によって話が変わってくる。- まず自身が根の場合は
X = 0としてよい。 - 自身が左子の場合:
- 親の
Xを見る。 - 本体左パートより左子の方が大きい場合は親の
Xそのままでよい。 - そうでない場合、調整として
[親のWl] - Wlを足す。- 「本体左パートより左子の方が大きい」時、これは0になる。
- まとめると、
X = [親のX] + [親のWl] - Wl.
- 親の
- 自身が右子の場合:
- 左子と右子の間隔が1文字であることを考えると、
X = [左兄弟ノードのX] + [左兄弟ノードのW] + 1.
- まず自身が根の場合は
- 縦位置
-
本体左パート
- 縦位置はバウンディングボックスと同じで
yl = Y. - 横位置は
Xそのままではないが、Xに少し補正すればよい。 xl = X + Wl - wl
- 縦位置はバウンディングボックスと同じで
-
本体中央パート, 本体右パート - 縦位置は左パートと同じ
- 中央パートの横位置は
xc = xl + wl - 右パートの横位置は
xr = xc + 1 = xl + wl + 1
- 中央パートの横位置は
-
ジャンクション
- 横位置は
xj = xc - 縦位置は
yj = yc + hc + 1
- 横位置は
-
左コーナー・右コーナー
- 縦位置はジャンクションと同じ
- 横位置は、子ノードのパラメータで簡単に書ける。つまり
- 左コーナーは
xlc = [左子ノードのxc] - 右コーナーは
xrc = [右子ノードのxc]
- 左コーナーは
- 子ノードのxcのかわりにWr,Wlを使うこともできる。
- 左コーナーは
xlc = xc - [左子ノードのWr] - 1 - 右コーナーは
xrc = xc + [右子ノードのWl] + 1
-
ビーム - 縦位置はジャンクションと同じ
- 横位置は:
- 左ビームは
左コーナーの横位置 + 1 - 右ビームは
ジャンクションの横位置 + 1
- 左ビームは
- 横位置は:
(外部依存性をもつ)パラメータまとめ
ここまでで得られたパラメータの式のうち、自ノード内で完結しないものを表にまとめておく。
| パラメータ | 根 | 左子 | 右子 | 依存性 |
|---|---|---|---|---|
| バウンディングボックス縦位置Y | 0 | [親のY] + [親のh] + 1 | 親:Y,h | |
| バウンディングボックス横位置X | 0 | [親のX] + [親のWl] - Wl | [左兄弟のX] + [左兄弟のW] + 1 | 親:X,Wl 左兄弟:X,W |
| バウンディングボックス高さH | 3 + (1 or 0) + max([左子ノードのH], [右子ノードのH]) | 左子:H 右子:H | ||
| バウンディングボックス左パート幅Wl | max(wl, [左子ノードのW]) | 左子:W | ||
| バウンディングボックス右パート幅Wr | max(wr, [右子ノードのW]) | 右子:W | ||
| バウンディングボックス幅W | Wl + 1 + Wr | (左子:W, 右子:W) | ||
| 左コーナー横位置xlc | [左子のxc]またはxc - [左子のWr] - 1 | 左子:xc(or Wr) | ||
| 右コーナー横位置xrc | [右子のxc]またはxc + [右子のWl] + 1 | 右子:xc(or Wl) | ||
「依存性」列には、そのパラメータが自ノード外の何に依存しているかを記載している。
各パラメータは、これらの式(+自ノード内で完結するものの式)すべてを連立方程式として解くことで得られる。
いや式多いだろ
そうだね。
そうだねじゃなくて
落ち着けって。
どーすんの!
パラメータ間の依存性は一見とても複雑(に見えるかもしれない)。
しかし、パラメータの表をよく眺めてみると、親と子すべてに同時に依存しているようなものは見つからない。
そのため、線形代数的な手法でがんばらずとも、比較的シンプルな方法でこの連立方程式は解けてしまう。
木のツアー
根から始めて、木のすべてのエッジを2度(下りと上り)ずつ通ってすべてのノードを訪問することを考える。
たとえば下図のような「ノード"Afterschool"を根とする部分木」があるとする:

青矢印は下りの、赤矢印は上りの移動を示している。
また青の数字はそのノードへの「最初の訪問」(prefixタイミング)の順番を、
赤の数字は「最後の訪問」(postfixタイミング)が起きる順番をそれぞれ表している。
少し考えると、
- prefixタイミングでは「親の位置」と「左兄弟ノードの位置とサイズ」、
- postfixタイミングでは「左右の子の位置とサイズ」
がそれぞれ確定していることがわかる。
従って、
- prefixタイミングでは
- バウンディングボックス位置
X, Y
- バウンディングボックス位置
- postfixタイミングでは
- バウンディングボックス高さ
H, バウンディングボックス横幅Wl, Wr, W, 左コーナー横位置xlc
- バウンディングボックス高さ
の依存先が確定している。言い換えるとこれらのパラメータが単純に計算できる。
コード
あとはプログラムに落とし込むだけや!!!
・・・ということで抜粋。
言語は諸事情によりGoで。
データ構造
二分木は以下のStructで表す。
// breee.Node
type Node struct {
// 親ノード
Parent *Node
// 左子ノード, 右子ノード
Left, Right *Node
// データ(文字列)
Data string
// 識別子
Id string
// オプション
Option map[string]string
}
レイアウト用のデータは別のStructが担当する。
type visualData struct {
// 元の木のノード
node *btree.Node
// ノードが持つ文字列の文字数
datasize int
// 本体左パートの幅, 本体右パートの幅
leftContentWidth, rightContentWidth int
// 本体セクションの幅
contentWidth int
// バウンディングボックスの幅, 中心のX, 左のX
width, center, left int
// バウンディングボックスの高さ, 中央のY, 上のY
height, top, middle int
// バウンディングボックス左の幅, バウンディングボックス右の幅
leftBboxWidth, rightBboxWidth int
// 未使用
lowerHeight, upperHeight int
// 表示用
prefix, suffix string
}
レイアウト処理
Struct VerticalLayoutがレイアウトを担当する。
レイアウトをする関数はlayout.
func (l *VerticalLayout) layout(v *visualizer) {
l.v = v
if v.root != nil {
l.fixLayout()
l.deployNodes()
}
}
fixLayoutでレイアウトを決定し、deployNodesで表示のためのデータを作成している。
func (l *VerticalLayout) fixLayout() {
v := l.v
l.fixSize()
l.fixPosition()
v.height = v.root.TreeHeight() * 4
v.width = v.data(v.root).width
}
fixSizeではW, Hなどのサイズパラメータ(→ 子ノードに依存)を決定し、
fixPositionではX, Yなどの位置パラメータ(→ 親と兄弟ノードに依存)を決定している。
func (l *VerticalLayout) fixSize() {
v := l.v
v.root.ApplyPostOrder(func(n *btree.Node, level, _ int) {
datasize := datasizeFor(n.Data)
// contentWidth は左右の │ を含む
leftContentWidth := datasize/2 + 1
rightContentWidth := (datasize - 1) - datasize/2 + 1
contentWidth := leftContentWidth + 1 + rightContentWidth
leftChildBboxWidth := v.data(n.Left).Width()
rightChildBboxWidth := v.data(n.Right).Width()
leftBboxWidth := max(leftContentWidth, leftChildBboxWidth)
rightBboxWidth := max(rightContentWidth, rightChildBboxWidth)
bboxWidth := leftBboxWidth + 1 + rightBboxWidth
d := &visualData{
node: n,
datasize: datasize,
height: 3,
width: bboxWidth,
left: 0, center: 0, top: level * 4,
leftContentWidth: leftContentWidth,
rightContentWidth: rightContentWidth,
contentWidth: contentWidth,
leftBboxWidth: leftBboxWidth,
rightBboxWidth: rightBboxWidth,
}
d.parseOption(n.Option)
v.dataMap[n] = d
})
}
func (l *VerticalLayout) fixPosition() {
v := l.v
v.root.ApplyPreOrder(func(n *btree.Node, _, _ int) {
d := v.data(n)
if n.Parent == nil {
// is root
d.top = 1
d.center = d.leftBboxWidth
} else if n.Parent.Left == n {
// is left child
d.top = v.data(n.Parent).top + v.data(n.Parent).height + 1
d.center = v.data(n.Parent).center - d.rightBboxWidth - 1
} else {
// is right child
d.top = v.data(n.Parent).top + v.data(n.Parent).height + 1
d.center = v.data(n.Parent).center + d.leftBboxWidth + 1
}
d.left = d.center - d.leftBboxWidth
})
}
処理中に登場する関数ApplyPostOrder, ApplyPreOrderは,
木を訪問しながら与えられた関数をpostfixタイミング,prefixタイミングで適用していく。
よって、fixSizeはpostfixタイミングでサイズを決めていき、その後fixPositionがprefixタイミングで位置を決めていく。
(文章での説明と異なり、ツアーを2回やっている。なぜ異なるかというとコードが古いから!!)
描画データ生成処理
時間がないので罫線素片を使って頑張るだけなので省略。
具体例
次のようなCSVで木を定義する。
1,apple,2,3
2,banana,,
3,cream,,
各行フォーマットはノード番号,文字列,(optional)左子のノード番号,(optional)右子のノード番号.
このファイルを表示させると、こうなる↓

もう少し大きなツリーを用意する。
1,apple,2,3,style,bold
2,banana,4,,color,green
3,cream,,,style,underline
4,dolce,5,6,color,red,style,strike
5,eel,,,style,italic
6,foiegras,,,style,invert
こちらはフォーマットに若干の追加要素がある:
ノード番号,文字列,(optional)左子のノード番号,(optional)右子のノード番号,[オプション名,設定内容]*.

ちゃんと描けてそうである。
1,チーズクリーム,2,3,style,bold
2,オイルフォンデュ,4,,color,green
3,りんご飴,7,,style,underline
4,サモサ,5,6,color,red,style,strike
5,桃,,,style,italic
6,青椒肉絲,,,style,invert
7,ザジキ,,
日本語だっていける。このあたりはGo様様である。

ちなみに、本記事冒頭の画像は、C++ std::setのコピー品の内部構造(赤黒木)を可視化したものである。
この後の話
まだまだ遊べそうなネタはある。たとえば
-
異なるレイアウトアルゴリズムを使う
- 今は上から下に書いているが、下から上にしたり、左から右にしたり。
- 子が1つしかない場合もっとシンプルな表示にする。
- パディングなどを柔軟に設定する。
-
N分木に対応させる
- そんなに難しくないと思われる。
-
要素の追加・削除に対して「頑健」にする
- 今のレイアウトアルゴリズムでは、要素が1つ追加あるいは削除された場合にも全体の様相が大きく変わることがある。
- そういうことが起こりにくいようなアルゴリズムにできると、ツリーの変化を可視化しやすくなるだろう。
まあ、やってないんですけどね・・・