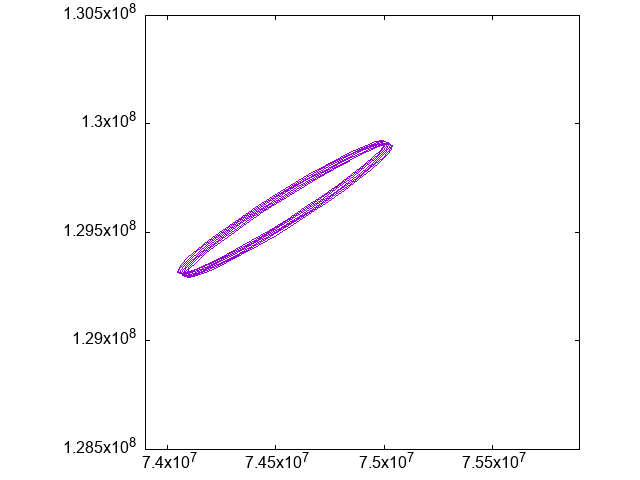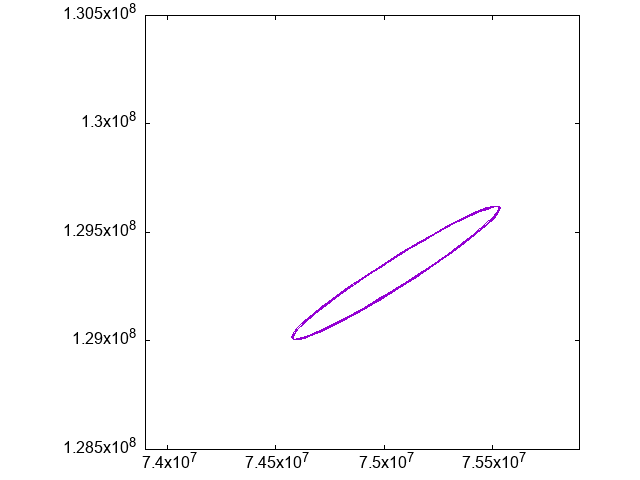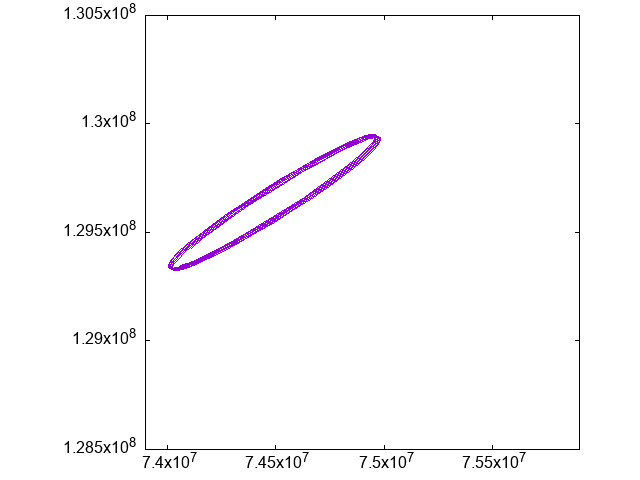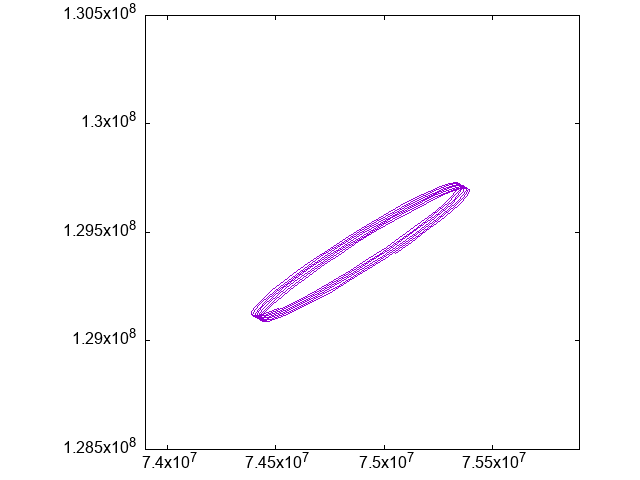Preamble
こんにちは、42tokyo Advent Calendar 2021 の17日目を担当する、在校生のyokawadaです。
42Tokyoでは主にツッコミ待ちをしています。
元々は別のネタを書いていたのですが、長さ的にAdvent Calendarにまったくもってふさわしくないことに気がついたため、古いネタを引っ張り出してきました。
実はこのネタ、筆者が初めてC言語に触れた大学時代の授業の課題ほぼそのままです。
(題材自体は自由選択でしたが。)
三体問題とは?
この世界に存在する物体の動きは、力学的な法則に従っていると考えられています。
力にはさまざまな種類がありますが、宇宙において支配的なのは重力です。
重力は非常に身近な力であり、その法則も(古典的には)単純ですが、重力による運動はとても複雑になりえます。。
例えば、3つの物体が互いに重力で引き合う時の運動(=重力三体問題)ですら、正確な予測は極めて困難です。
ですが、コンピュータを使うことで、我々はその難解さにある程度立ち向かうことができます。
この記事では、その一端をお手軽に体験することを目的とします。
(絵だけ見たい人はここをクリックだ!)
ソースコード
こちら(C言語です)↓
https://github.com/corvvs/graint
お手元の環境で動作しない場合はお知らせください。
そしたら私へ〜って言いますから
前説(1) 重力ってどんなもの?
重力「相互」作用
重力とは、雑に言うと、「重さを持つもの同士が引っ張り合う力」です。
正確には重さではなく質量で、質量に対して重力が働くことで、そこに重さが生じます。
たとえば、あなたがその辺の本を手にとって持ち上げると、手に重みを感じるはずです。
これは、本の質量に対して、地球の質量による重力が働いているからです。
感じる重みの正体は、「本に働く重力・・・によって本があなたの手を押す力」に逆らってあなたが物体を持ち上げる力です。
質量は重力を感じると共に、重力を生み出します。
本に働いている重力は、ほとんどが地球によるものです。
ですがそれだけではなく、月、太陽、その他の惑星による重力も、僅かながら作用しています。
さらに、周囲の存在する、質量を持つあらゆる物体(あなた自身を含む)が生みだす重力も、極めて微量ですが、ちゃんと働いています。
それら全ての重力の合計が、あなたが手に感じる重みです。
重力の向きと大きさ
上述の通り、質量を持った2つの物体は、互いに重力を及ぼしあいます。
ある物体が別の物体から受ける重力の性質は:
- 大きさは自分の質量に比例する。
- 大きさは相手物体の質量にも比例する。
- 大きさは自分と相手の距離の2乗に反比例する。
- (向きは、自分と相手を結ぶ直線に沿っていて、相手の方に引っ張られる。)
以上を数式にまとめると、自分の質量を$m$, 相手の質量を$M$, 自分と相手の距離を$R$として、重力の大きさは
$$G\frac{Mm}{R^2}$$
と表現できます。
$G$は適当な比例定数で、万有引力定数と呼ばれます。

力の向きは、上図の通り、発生源である質量のある方へ引っ張る向きになります。
我々はおおむね地球の表面で生活しています。
地球の表面付近における地球による重力の大きさは、$M$に地球の質量$M_E$、$R$に地球の半径$r_E$を代入すると
$$G\frac{mM_E}{r^2_E} = m\frac{GM_E}{r^2_E} = mg$$
となります。
$g$は各種教科書でおなじみ?の9.8$m/s^2$(メートル毎秒毎秒)です。
https://www.google.com/search?q=%E4%B8%87%E6%9C%89%E5%BC%95%E5%8A%9B%E5%AE%9A%E6%95%B0+*+%E5%9C%B0%E7%90%83%E3%81%AE%E8%B3%AA%E9%87%8F+%2F+(%E5%9C%B0%E7%90%83%E3%81%AE%E5%8D%8A%E5%BE%84^2)
前説(2) 重力が引き起こす運動
運動方程式
ここで少し話を変えます。
高校で物理という科目を始めて勉強するとき、その最初の方に「運動方程式」が登場します。
運動方程式は、「**物体に力をかけると、その分だけ動く」**という日常的な感覚を数式で表したものです。
日本語で表現すると
$$質量 \times 加速度 = 力$$
といった感じになります。
いわゆる$ma = F$ですね。
$m$は質量(mass), $a$は加速度(acceleration), $F$は力(Force)を表します。
$ma = F$の両辺を$m$で割ると$a = F/m$となります。
日本語で書くと
$$加速度 = 質量あたりの力$$
でしょうか。
この式が全ての鍵になります。
(ここから「微分」と「積分」が登場します。アレルギーをお持ちの方はご注意。)
さて、加速度とは「速度の時間変化」、つまり速度を時間で微分したものです。
微分と積分は互いに逆の演算なので、加速度を時間で積分すると速度になります**。**
同様に速度は「位置の時間変化」、つまり位置を時間で微分したもので、
従って同様に、速度を時間で積分すると位置になります。
以上をまとめると、加速度を時間で2回積分したものは位置になると言えます**。**
ということで、運動方程式 $a = F / m$ の右辺(質量当たりの力)を頑張って2回時間で積分すれば、位置がわかることになります。
重力二体問題
https://ja.wikipedia.org/wiki/二体問題
「質量を持った2つの物体は、互いに重力を及ぼし合う」という冒頭の話に戻ります。
宇宙にはこの2つ物体以外何もないとすると、これらの物体の運動は、互いの重力だけで決まることになります。
これらをそれぞれ物体1、物体2とし、文字を
- 物体1の質量 $m_1$
- 物体1の位置ベクトル $r_1$
- 物体2の質量 $m_2$
- 物体2の位置ベクトル $r_2$
- 時刻 $t$
- 万有引力定数 $G$
と定義します。
すると、運動方程式は
$$
\frac{d^2r_1}{dt^2} = -G\frac{m_2}{|r_1 - r_2|^2}\frac{r_1 - r_2}{|r_1 - r_2|} \\
\frac{d^2r_2}{dt^2} = -G\frac{m_1}{|r_2 - r_1|^2}\frac{r_2 - r_1}{|r_2 - r_1|} \
$$
の2式の組になります。
2式の差を取ると、
$$\frac{d^2}{dt^2}(r_1 - r_2) = - G\frac{m_1 + m_2}{|r_1 - r_2|^2}\frac{r_1 - r_2}{|r_1
- r_2|}$$
となり、$r_1 - r_2 = s$ と読み替えると、
$$\frac{d^2s}{dt^2} = -\frac{G(m_1 + m_2)}{|s|^2}\frac{s}{|s|
}$$
と、1つのベクトル変数$s$に対する式(微分方程式)になります。
これはちゃんと厳密に解くことができて、$s$の軌道は楕円・放物線・双曲線のうちいずれかになります。
解き方はググっとくれ
では三体だと?
https://ja.wikipedia.org/wiki/三体問題#求積不可能性 (読める人は読んでください。筆者には読めません。)
二体の場合は、初期条件には特に関係なく、積分を使って厳密に解くことができます。
しかし、これが三体になると、特殊な初期条件を除いて厳密に解くことが絶望的に難しくなります(不可能、とは言い切られていないが、人類側の勝ち筋は封じられている)。
もちろん三体より多い場合も同様です。
・・・そんなわけで、「数値積分」の出番です。
本題 数値積分
数値積分とは、積分をきちんと解かずに定積分の値を計算する方法のことです。
これを使って、運動方程式の「加速度を時間で2回積分」します。
オイラー法
オイラー法は、数値積分としてはとてもわかりやすい手法です。
まず、微分係数の定義から出発します:
$$\lim_{\Delta t \rightarrow 0}\frac{f(t + \Delta t) - f(t)}{\Delta t} = f'(t)$$
左辺の極限を0に達する前に止めて、$\Delta t$を有限の大きさのままにします:
$$\frac{f(t + \Delta t) - f(t)}{\Delta t} \sim f'(t)$$
$\sim$は「だいたい等しい」という意味だと思ってください。
この記事ではその辺雑に扱います。
さらに、$f(t + \Delta t)$以外のものをすべて右辺に移すと、
$$f(t + \Delta t)\sim f(t) + f'(t)\Delta t$$
関数$f$の$()$の中身に注目すると、
左辺では$t + \Delta t$, つまり少し未来の量なのに対し、右辺は$t$のみ、つまり現在の量のになっています。
また$\Delta t$はこちらで決めてよい値です(なるべく小さくする必要はありますが)。
よって、現在の$f(t)$およびその微分係数$f'(t)$の値がわかれば、それらだけを使って少し未来の量を予測できることになります。
これを運動方程式$dv/dt = F(r)/m$に適用するときは、
- $r(t + \Delta) = r(t) + v(t)\Delta t$
- $v(t + \Delta) = v(t) + \frac{1}{m}F(r(t))\Delta t$
という手順で位置と速度を少しずつ予測していくことになります。
リープフロッグ法
https://ja.wikipedia.org/wiki/リープ・フロッグ法
リープフロッグ法は、オイラー法とは別の角度から予測を行う手法です:
$$\begin{array}{rcl}
r_1(t + \Delta t) & = &
r_1(t) + v_1(t)\Delta t + \frac{1}{2}F_1(r_1(t), r_2(t), r_3(t))\Delta^2
\\
v_1(t + \Delta t) & = &
v_1(t) \\
&+& \frac{1}{2}\left[
F_1(r_1(t), r_2(t), r_3(t))
\right.
\\
&+&
\left.
F_1(r_1(t+\Delta t), r_2(t+\Delta t), r_3(t+\Delta t))
\right]\Delta t
\\
\end{array}$$
書いていると時間がいくらあっても足りないので、詳細は割愛しますが、重要な性質にだけ軽く触れておくと、リープフロッグ法においては保存則が近似的に成り立ちます。
たとえば「エネルギー保存側」といった単語を聞いたことがあるかもしれませんが、リープフロッグ法を使う場合、「エネルギーのようなもの」が近似的に保存します。
エネルギー以外の保存量についても同様です。
これはオイラー法およびその仲間の手法にはない性質です。
ソースコード(抜粋)
ソースコードについて少しだけ説明します。
まずはmainから。
int main()
{
t_system system;
t_system_initializer *initializer = initsystem_lagrange4;
t_system_expander *expander = expand_leap_frog;
t_system_printer *printer = print_system;
initializer(&system);
print_profile(&system);
run(&system, expander, printer);
}
構造体t_systemはシミュレーションの設定 + 現在の状態を保持する構造体です。
各物体の情報もt_systemが持っています。
initializer, expander, printerは関数ポインタで、それぞれ:
-
initializert_systemの初期値設定 -
expander運動の予測(時間発展) -
printer運動の様子の出力
を担当する関数が入っています。
具体的なexpanderとして、オイラー法で運動を予測する関数を示します:
// オイラー法による時間発展
void expand_euler(t_system *system)
{
t_vector3 f;
t_vector3 f1 = accel(system->m2, &system->r1, &system->r2);
t_vector3 f2 = accel(system->m3, &system->r2, &system->r3);
t_vector3 f3 = accel(system->m1, &system->r3, &system->r1);
f = accel(system->m3, &system->r1, &system->r3);
vector_add(&f1, &f1, &f);
f = accel(system->m1, &system->r2, &system->r1);
vector_add(&f2, &f2, &f);
f = accel(system->m2, &system->r3, &system->r2);
vector_add(&f3, &f3, &f);
t_vector3 v;
// 1
// v = v1
v = system->v1;
// v = v * dt
vector_mul(&v, &v, system->dt);
// r1 = r1 + v
vector_add(&system->r1, &system->r1, &v);
// f1 = f1 * dt
vector_mul(&f1, &f1, system->dt);
// v1 = v1 + f1
vector_add(&system->v1, &system->v1, &f1);
// 2
v = system->v2;
vector_mul(&v, &v, system->dt);
vector_add(&system->r2, &system->r2, &v);
vector_mul(&f2, &f2, system->dt);
vector_add(&system->v2, &system->v2, &f2);
// 3
v = system->v3;
vector_mul(&v, &v, system->dt);
vector_add(&system->r3, &system->r3, &v);
vector_mul(&f3, &f3, system->dt);
vector_add(&system->v3, &system->v3, &f3);
}
構造体t_vector3は3次元のベクトルを表現するもので、double型の要素x, y, zを持ちます。
vector_add, vector_mulはそれぞれベクトルの加算と定数(スカラー)倍を行う関数です。
また、途中に何度か登場するaccel関数は、質量あたりの重力(=加速度)を計算します。
コードはこうです:
# define G 4.98217402e-10 // [km^3kg^-1day^-2]
// 質点youによる質点meへの質量あたりの重力ベクトル
t_vector3 accel(double m_you, t_vector3 *r_me, t_vector3 *r_you)
{
t_vector3 a;
vector_sub(&a, r_me, r_you);
double norm3 = pow(vector_norm(&a), 3);
double f = -G * m_you / norm3;
vector_mul(&a, &a, f);
return a;
}
引数はそれぞれ:
-
m_you重力を及ぼす側の質量 -
r_me重力を及ぼされる側の位置ベクトル -
r_you重力を及ぼす側の位置ベクトル
といった意味です。
関数vector_subは2つの3次元ベクトルの引き算を計算します。
また、式の途中に登場するGは万有引力定数です。
一般的によく知られている値とは異なりますが、これはプログラムにおける長さと時間の単位を、より扱いやすいものに設定してあるためです。
シミュレーション色々
以下、基本的にリープフロッグ法を使います。
いくつか初期条件を変えてシミュレーションを行いますが、
それぞれの初期条件はgitリポジトリ内のinitializer.cファイル内にまとめて入っているので、興味のある方は探してみてください。
太陽・地球・月(楕円軌道)
まずは、太陽・地球・月と同じような動きをさせてみます。
3つの物体の質量と初期位置をそれっぽく設定し、速度も適当にいじります:
void initsystem_solar(t_system *system)
{
*system = (t_system){
// 1ステップあたりの時間; 0.001日 = 86.4秒
.dt = 0.001,
// ステップ総数
.n = 1000000ull,
// 現在のステップ数; これは変数
.i = 0,
// 出力頻度; 出力関数を何ステップに1回呼び出すか?
.output_period = 1,
// 「太陽」の質量、位置、速度
.m1 = 1.98892e30,
.r1 = {0, 0, 0},
.v1 = {0, 0, 0},
// 「地球」の質量、位置、速度
.m2 = 5.972e24,
.r2 = {1.5e8, 0, 0},
.v2 = {0, 2.566080e6, 0},
// 「月」の質量、位置、速度
.m3 = 7.34581e22,
.r3 = {1.5e8 + 3.84400e5, 0, 0},
.v3 = {0, 2.6550580e6, 0},
};
}
前述した通り、質量の単位はkg, 距離の単位はkm, 時間の単位は(地球)日です。
これらはあくまで「それっぽい」値で、現実の太陽系を忠実に再現しているわけではありません。
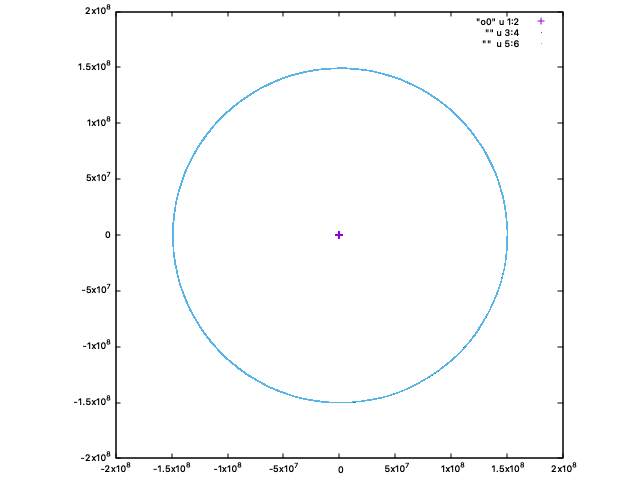
そのため、運動の様子も微妙に異なります。
紫の十字が「太陽」です。
「地球」は緑の、「月」は青の点ですが、ほぼ同じ軌道を動くため、このスケールだと重なってしまい区別できません。
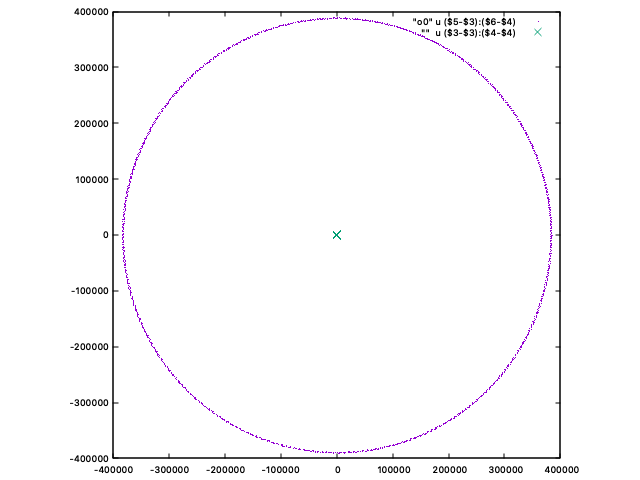
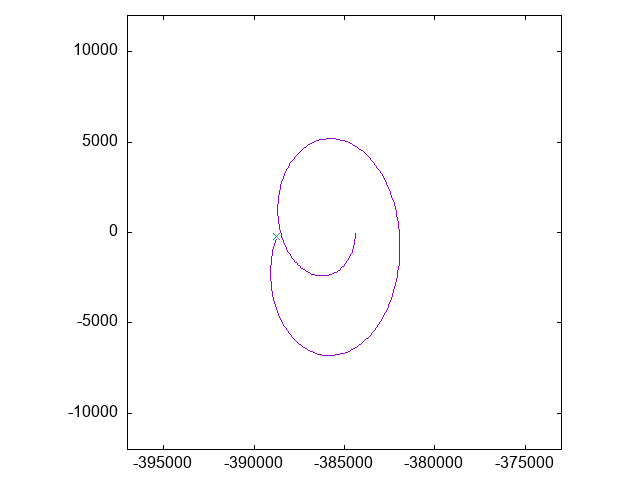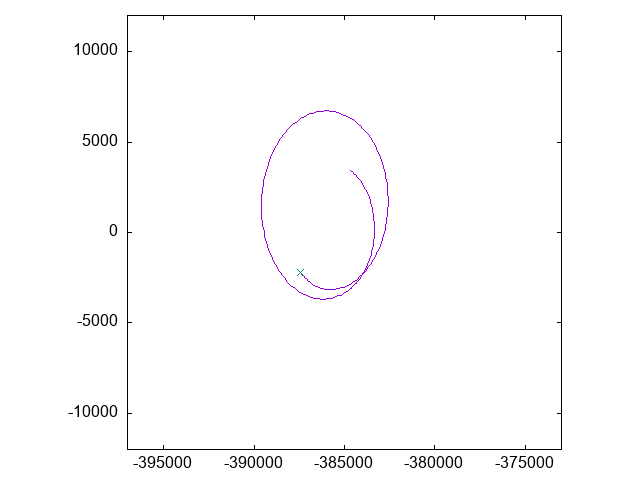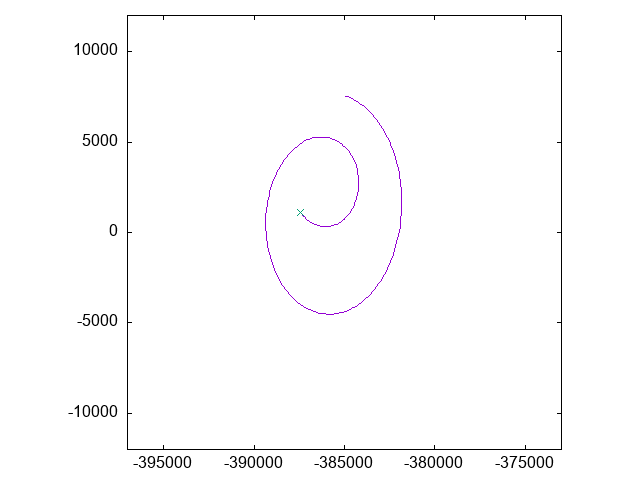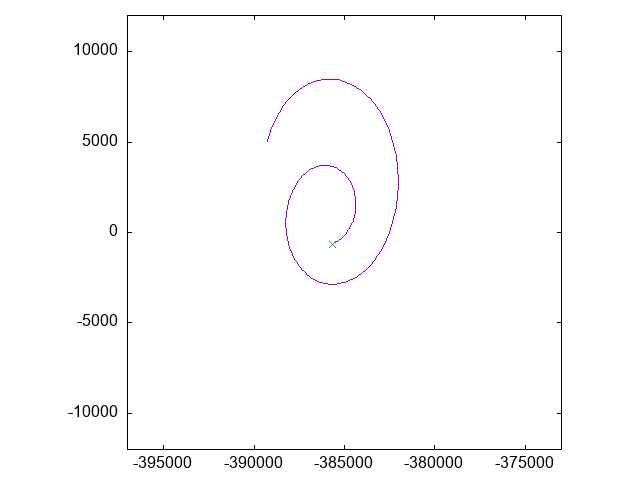
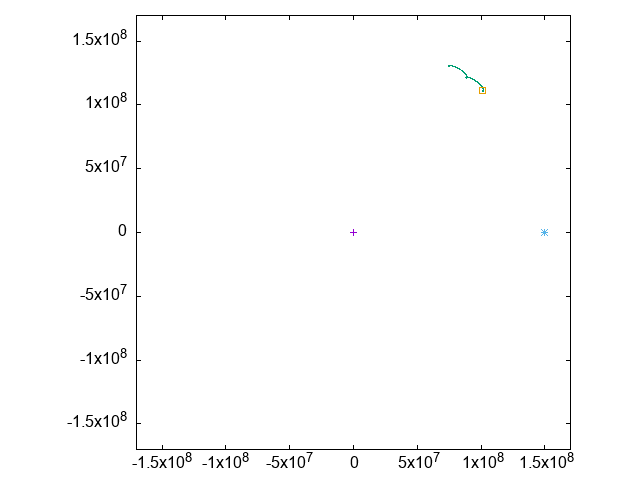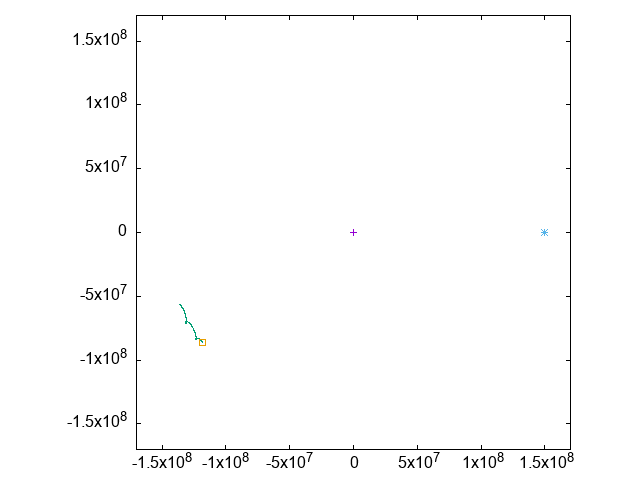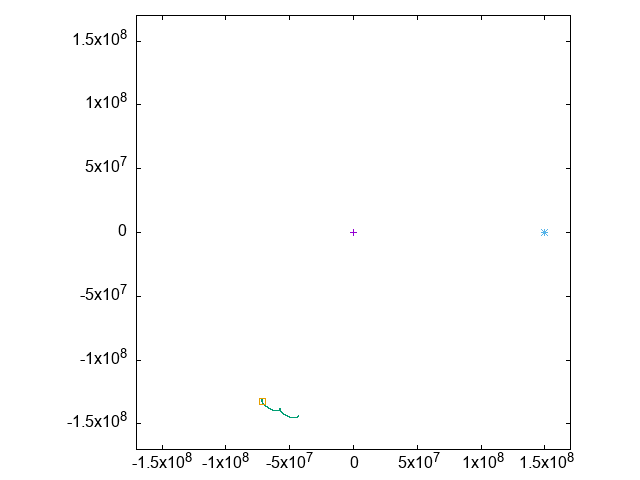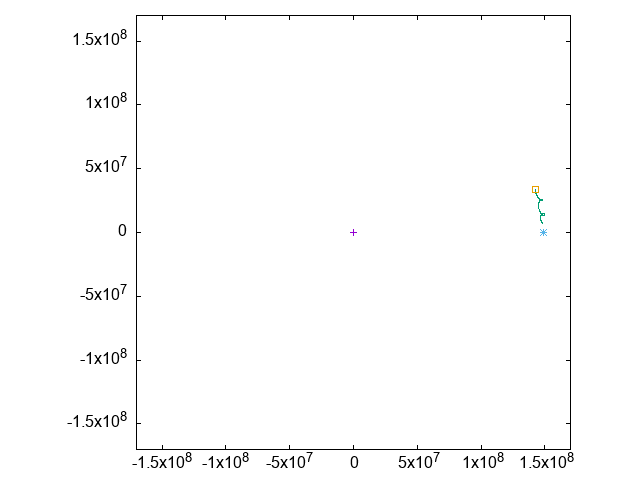
そこで、「地球」を中心とする座標に移り、「地球」と「月」の運動だけを表示すると、こうなります:
今度は紫の点が「月」で、中央のクロスマークが「地球」です。
先ほどとほとんど同じような見た目ですが、目盛の数字が違います。
「月」が「地球」の周囲でほとんど円形に運動していることがわかります。
現実の月の平均公転半径はおよそ385000kmで、円の半径もおおよそそれくらいです。
(※以下、有効数字は適当です)
プログラムの出力結果から、「地球」が「太陽」を周回する運動の角速度(極座標表示において、角度の単位時間あたりの変化量)を求めると、およそ 0.0172ラジアン/日(または、0.985度/日)になります。
周期(角度が一周するのにかかる時間)に換算すると365.3日になります。意外といい値ですね。
同様に、「月」が「地球」を周回する運動の角速度も計算してみます。
ただしこの時、「地球」から見た「太陽」の向きを固定して考えます。
すると、角速度は0.211ラジアン/日(または 12.1度/日)となり、周期に換算すると29.7日となります。
これまた意外といい値です。
この角速度を使って、「月」の細かい動きを観察してみます。
「地球」から見た「太陽」の向きを固定して考えた座標系、を基準にしてさらに、
『「月」が「地球」を周回する運動の角速度』で回転する座標系を考えます。
この座標系で見ると、「月」は「地球」に対してほぼ固定されるはずです。
・・・ややこしいですが、そうなんです。
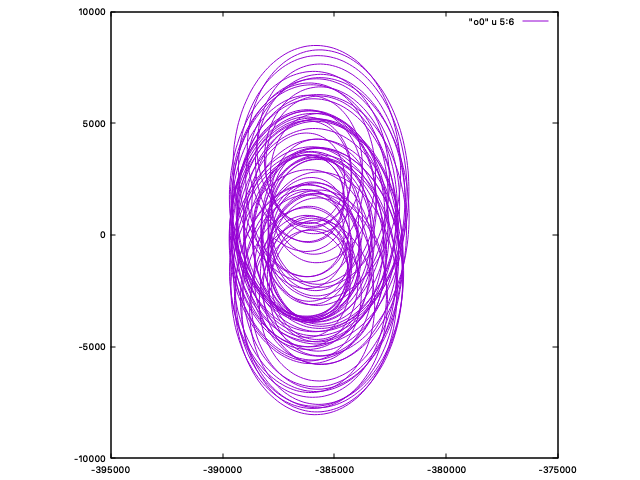
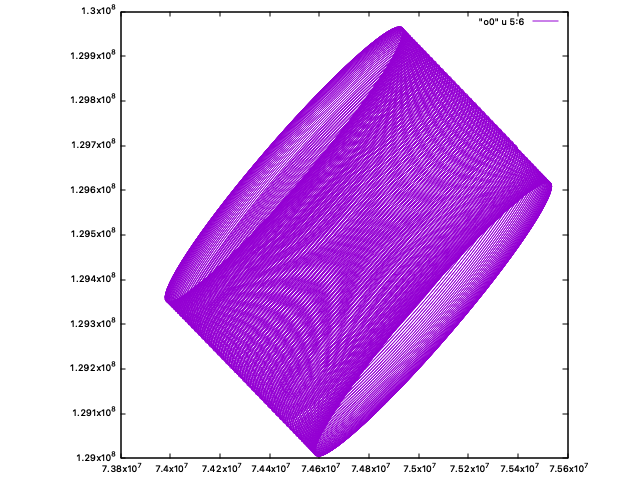
で、実際にその座標系での「月」の動きをアニメーションにしたものがこちら:
グラフの横軸は地球からの距離(km)で、縦軸は「固定点からのずれ」です。
「月」は、固定点の周りのある狭い範囲で細かく円状に動いていることがわかります。
これは、実際の月の運動における「経度秤動」に相当するものと思われます。
(ただ、実際の経度秤動よりもすこし動きが大きいようです。初期値の差によるもの?)
静止画はこちら:
三重連星
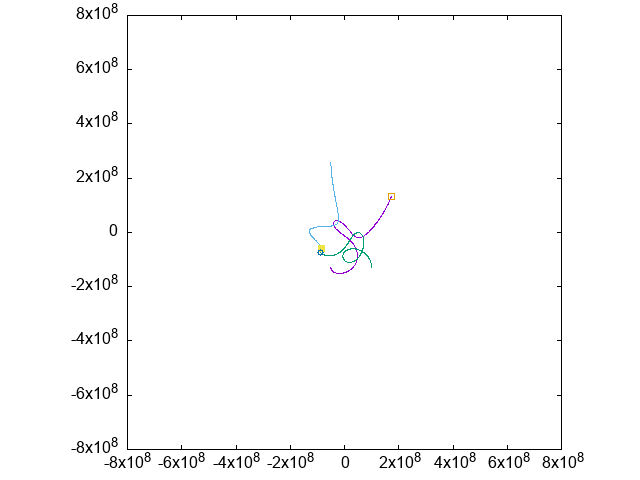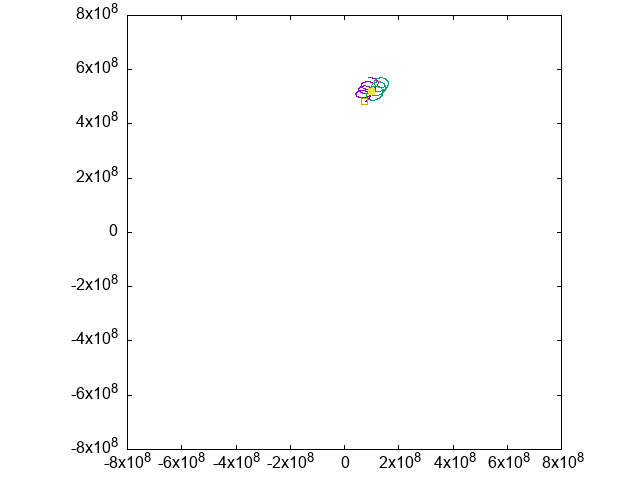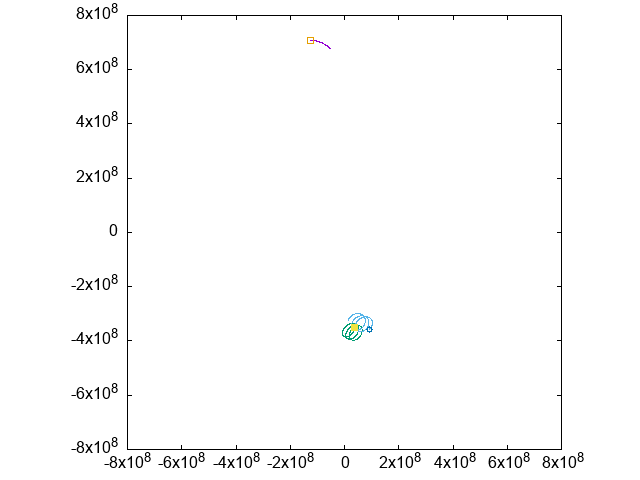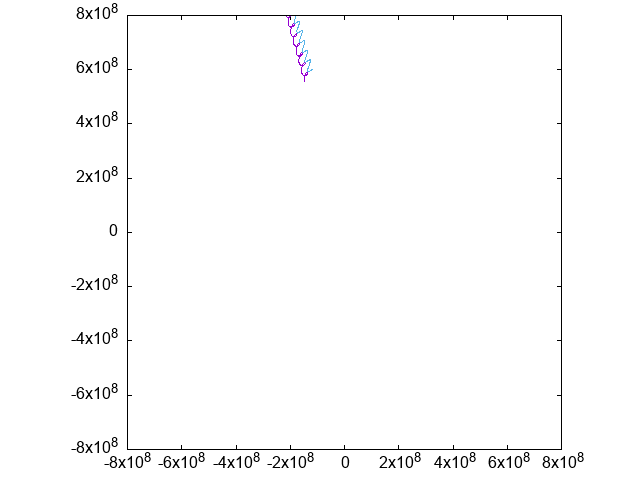
3つの物体の質量をほぼ同じにしてみました。
こんな星系には生まれたくないですね。
この運動を静止画にすると、下のようになります:
近所のスーパーのイラストコーナーによくこんなの貼ってあるわ
ラグランジュ4
三体問題においては、ラグランジュ点と呼ばれる特殊な配置が存在します。
ラグランジュ点は三体の位置関係について5パターンに分かれますが、そのうちラグランジュ4(L4)と呼ばれるものを再現してみました。
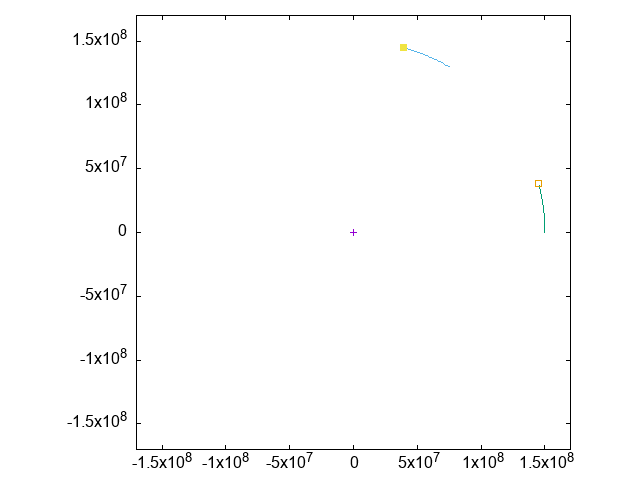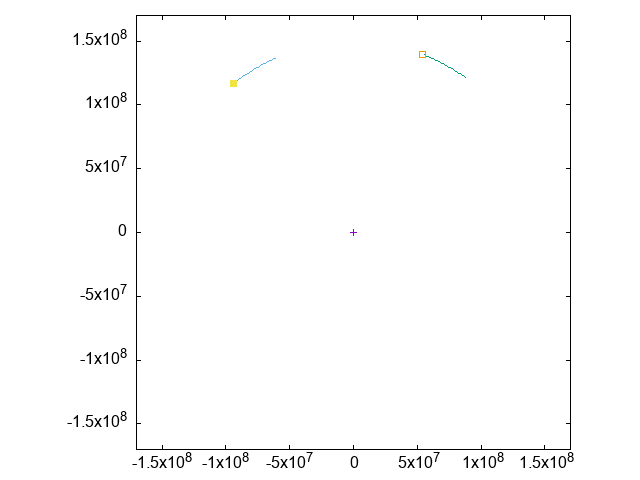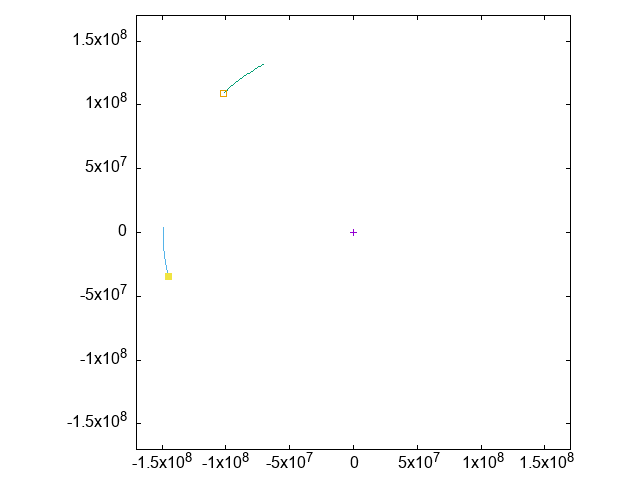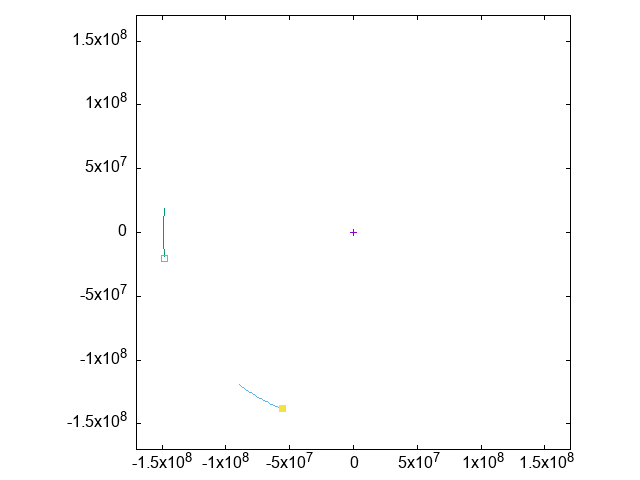
紫を中心とした(ほぼ)円軌道を、緑の軌跡と、それに先行するように青い軌跡が周回しています。
実は、紫・緑・青の3者は正三角形の配置を保っています。
これを観察するために、紫と緑の位置を固定(=実質動くのは青だけに)した視点で、青の位置だけをアニメーションさせてみます:
青(アニメーション図では紫)は、正三角形をなす点の周辺を、より細かい軌道を描いてうろうろしていることがわかります。
静止画だとこんな感じ。
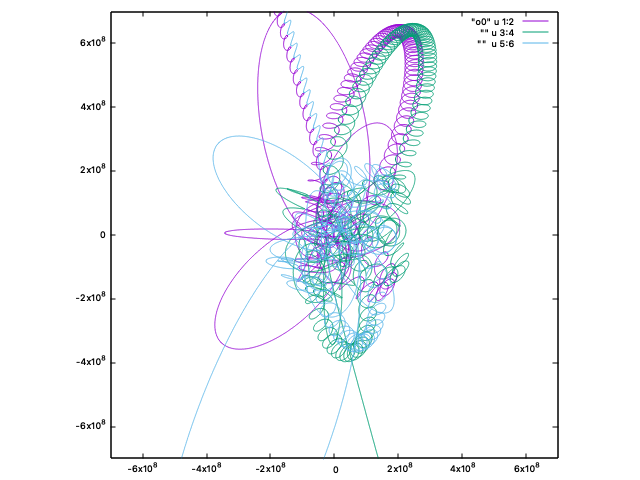
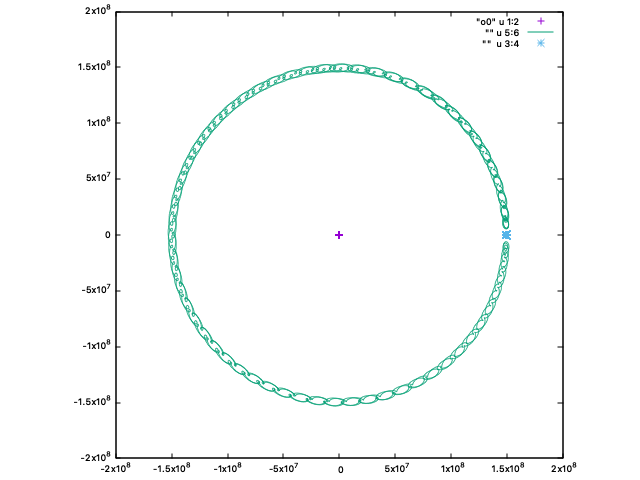
馬蹄型軌道
さて、1つ前のアニメーションのパラメータを少しだけいじります。
最初は同じような動きをしていますが、よく見ると実は
- 徐々に青と緑の距離が近づいていく
- やがて接触する・・・かと思いきや再び離れていく
- どんどん離れていったと思えば、一周回って逆側から近づき始める
- 今度こそ接触する・・・と思いきやまた離れていく
- 以下ループ
という動きになっています。
観察のため、紫と青の動きを固定してみます:
うねうねしてかわいいですね
緑の軌道が「視力検査のC」のようになっていることがわかります。
紫を太陽、青を地球とした時の緑にあたる動きをする天体が、実際にいくつか存在することが知られています。
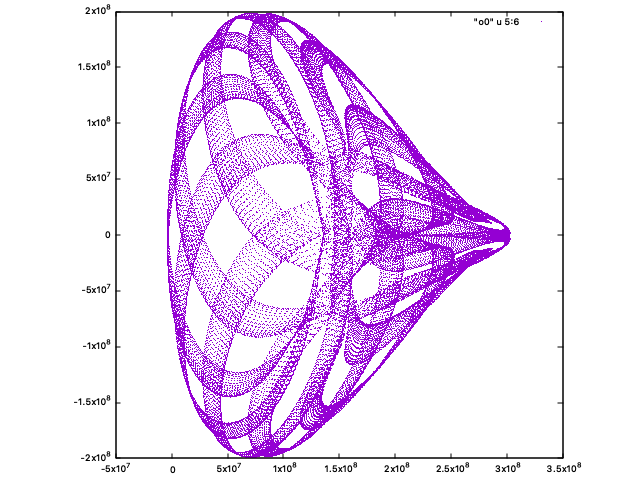
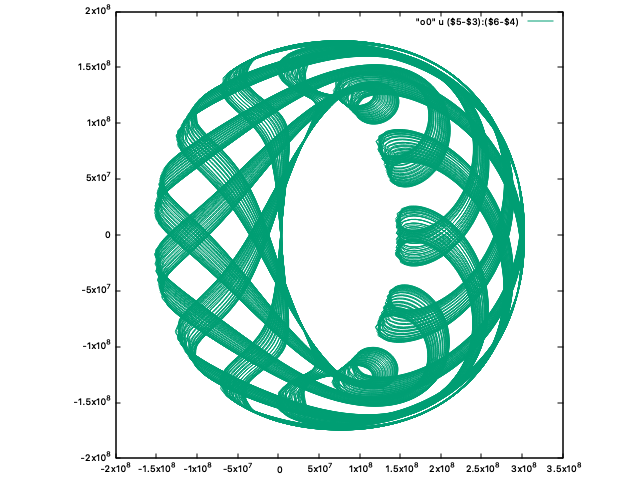
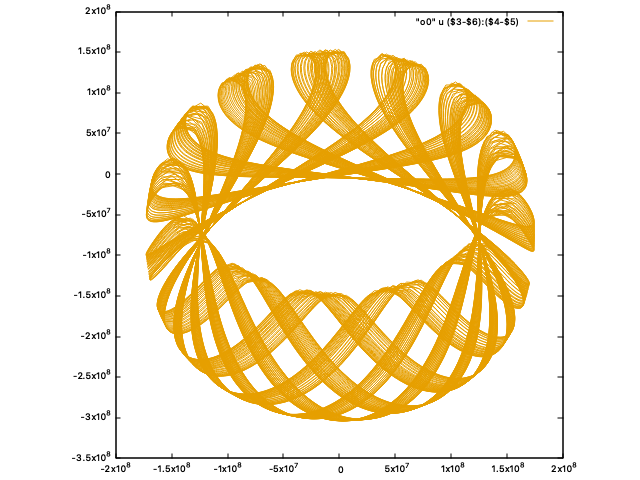
その他、印象的な画像集
宝石みたい
こっちはリンゴを保護するアレみたい
パスタ感
(物理的に意味のない変換をしています)
締め
たいへん駆け足でしたが、この辺で終わりにしておきます。
興味のある方は、GitHubにコードがあるのでぜひいじってみてください。
無限に時間が溶かせます。
Postamble
明日は、rmatsukaさんが42での奇妙な冒険について書いてくれる予定ですので、そちらの記事もお楽しみに!
最後までお読みいただきありがとうございました。
ところで締めとPostambleって意味かぶってない?