この記事は自然言語処理 #2 Advent Calendar2019の2日目の記事です。
はじめに
この記事では以下の論文から内容を抜粋して紹介しつつ、仮説検定のp値について述べます。
Not All Claims are Created Equal: Choosing the Right Approach to Assess Your Hypotheses
紹介する論文は、自然言語処理の論文を書く上での仮説検定(もしくはベイズ推論)を行う方法を述べたものです。とくに仮説検定のp値の解釈は難しく誤解されていることが多いため、より解釈しやすいベイズ推論も使うべきと主張しています。
ここでは検定のp値について理解することに集中し、具体的な検定やベイズ推論の方法は扱いません。
具体的な検定の仕方が知りたいなら、以下の論文が詳しいです。
The Hitchhiker’s Guide to Testing Statistical Significance in Natural Language Processing
仮説検定は提案手法の優位性を示すためによく用いられます。
(具体的には、提案手法と既存手法の性能が同じであるという帰無仮説を検定し、$ p < 0.05 $ なら2つの手法の性能差は統計的優位であると結論づける)
しかし検定のp値の意味は誤解されやすいので注意が必要です。
特に、以下の2つの記述はどちらも誤りです。
1. p < 0.05 のとき、帰無仮説が正しい確率は5%未満である。
2. p > 0.05 のとき、帰無仮説は正しい。
この記事を読めば、上の2つがなぜ誤りかを理解できるようになります(多分)。
自分はQiita記事を書くのが初めてなので読みにくいかもしれませんがご容赦ください。大学で統計を勉強したことがあるので仮説検定の話題を選びました。
仮説検定の基礎
p値を理解するために、まず仮説検定について復習します。
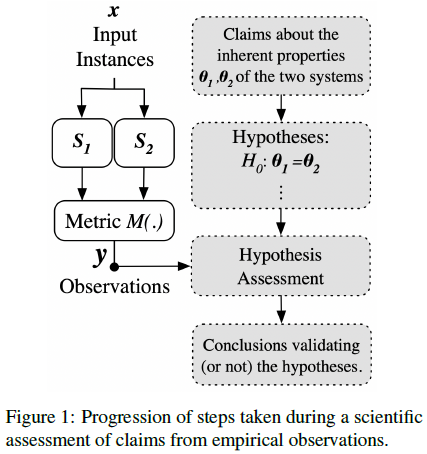
提案手法と既存手法は何らかのタスクに対してそれぞれ $ \theta_1, \theta_2 \in [0, 1] $ の精度が出るものとします。例えば手法が品詞推定のタスクなら、各単語に対して推定した品詞の正解率が $ \theta_1, \theta_2 $ です。
ここで、$ \theta_1, \theta_2 $ はそれぞれの手法に内在する真の精度(unknown inherent accuracy value)であり、データセットから計算されるような経験的な値ではありません。
今知りたいのは $\theta_1 > \theta_2$ が成り立つかどうか(つまり提案手法が既存手法を上回るといえるかどうか)です。
そのために次の帰無仮説 $ H_0 $ を考え、これを検定します。
H_0 : \theta_1 = \theta_2
この検定をするために観測値 $ \boldsymbol{y} $ を用います。これはデータセットを用いた実験結果を表していて、例えば品詞推定タスクの場合なら、データセット中の全ての単語に対する品詞推定の正誤の結果を集めたものです。
下図が仮説検定の流れを表しています。
検定のp値の定義を言葉で表すと、**「帰無仮説 $ H_0 $ が正しいと仮定したときに、観測値 $ \boldsymbol{y} $ 以上に珍しい値が出る確率」**です。
これを数式で表すためには「珍しさ」を定義する必要があり、それが検定統計量と呼ばれる関数 $ \delta(\cdot) $ です。
$ \delta(\boldsymbol{y}) $ の値が大きいほど観測値 $ \boldsymbol{y} $ が珍しいことを意味します。
p値の定義を数式で書くと以下になります。
p = P(\delta(Y) \ge \delta(\boldsymbol{y}) \mid H_0) \tag{1}
ここで $ Y $ はランダムに得られる観測を表す確率変数です。
品詞推定タスクの場合なら、$Y$ は未知のデータに対する品詞推定の正誤です。
もしこの値が 0.05 未満なら、帰無仮説が正しいという仮定の下では今得られた観測値 $\boldsymbol{y}$ はとても珍しい(確率 0.05 未満でしか起こらない)ということなので、そもそも仮定が間違っているだろうと結論付けられる、というわけです。
p値の2つの誤解を解く
検定のp値の定義を述べたところで、最初に挙げたp値の2つの誤解を解決します。
先ほどのp値の定義を用いれば、$ p < 0.05 $ は「帰無仮説 $ H_0 $ が正しいと仮定したときに、観測値 $ \boldsymbol{y} $ 以上に珍しい値が出る確率」が0.05未満であることを表すのでした。
1. p < 0.05 のとき、帰無仮説が正しい確率は5%未満である。
これが誤りである理由は、帰無仮説 $ H_0 : \theta_1 = \theta_2 $ はそもそも確率的な事象ではなく「何%の確率で正しい」という言い方自体ができないからです。
統計的仮説検定においては提案手法と既存手法の真の精度 $ \theta_1 , \theta_2 $ は(我々は知らないが)ある一つの値に定まっていて確率変数ではないと考えています。
2. p > 0.05 のとき、帰無仮説は正しい。
仮説検定において、p値が大きいときは何も言えることはありません。p値の定義に戻ると「帰無仮説 $ H_0 $ が正しいと仮定したときに、観測値 $ \boldsymbol{y} $ 以上に珍しい値が出る確率」が0.05より大きいということですが、これは帰無仮説 $ H_0 $ に"矛盾していない"観測が得られたというだけであって、$ H_0 $ を"積極的に採用する"根拠にはなりません。
というわけで、2つの主張が誤りであることが分かりました。
p値はその正確な定義が複雑であるために解釈が難しく、意味を誤解されがちです。
信頼区間について
p値の2つの誤解が解決したところで、信頼区間について少し述べておきます。
p値の定義が結構込み入っていて解釈しにくいということはもう述べましたが、信頼区間はそれ以上に解釈しにくいです。
ただし確実に言えることは、次の解釈は誤りだということです。「パラメータ $\theta$ が95%の確率で存在する区間が95%信頼区間である」
これは $\theta$ がある値に定まっている定数であって確率変数でないことから明らかです。1
しかし実用上、上記のような「パラメータ $\theta$ が95%の確率で存在する区間」を知りたいことはあります。それを可能にするのがベイズ推論です。
おわりに
いかにもこれからベイズ推論の話をする流れなのですが、これは仮説検定やp値の解釈の話とはまた別なので割愛します。気になる方は論文を参照してください。
結局、この記事では次のことだけ何回も強調していました。
仮説検定ではパラメータは確率変数ではなく、ある真の値をもつと考える。したがって、「帰無仮説が正しい確率」とか「パラメータがこの区間に入る確率」などという言い方はできない
ようするにp値や信頼区間の解釈はしづらく、誤解されやすいので気を付けましょうということです。
手法の統計的優位性を示すためにp値を使ってはいけないということではないです。適切な検定をしていれば全く問題ありません。2
本当はベイズ推論も含めてもっと網羅的に書きたかったのですが執筆力が足りず書けませんでした。修業します。