読んだときのメモ。間違いがあるかもしれません。図表はすべて論文より引用しています。
論文: https://proceedings.mlr.press/v119/katharopoulos20a.html
参考にした記事: https://qiita.com/Yosemat1/items/802a41588e8bffaca992
参考にした記事2: https://scrapbox.io/yuwd/Linear_Attention:_Transformers_are_RNNs
- Title: Transformers are RNNs: Fast Autoregressive Transformers with Linear Attention
- Authors: Angelos Katharopoulos, Apoorv Vyas, Nikolaos Pappas, François Fleuret
- Venue: ICML 2020
- 概要: Self-attentionをカーネル特徴関数の線形ドット積として表現することで計算量を$O(N)$に削減
- 問題設定 (Transformer)
- $x\in\mathbb{R}^{N\times F}$: $F$次元の特徴ベクトル$N$個
- Transformer: $T:\mathbb{R}^{N\times F}\to\mathbb{R}^{N\times F}$
- $L$層のTransformerについて、各層$T_1(\cdot),\dots,T_L(\cdot)$は$$T_l=f_l\left(A_l\left(x\right)+x\right)$$
- $f_l\left(\cdot\right)$: 各特徴を他の特徴から独立に変換 (通常は2層のFNN)
- $A_l\left(\cdot\right)$: Self-attention (系列を通して作用する) $W_Q\in\mathbb{R}^{F\times D}, W_K\in\mathbb{R}^{F\times D}, W_V\in\mathbb{R}^{F\times M}$$$\begin{align*}
Q&=xW_Q,\\
K&=xW_K,\\
V&=xW_V,\\
A_l(x)&=V^\prime=\text{softmax}\left(\frac{QK^\top}{\sqrt{D}}\right)V.\\
\end{align*}$$
- カーネルに基づいたSelf-attentionの定式化 (行列の結合法則を使用)$$V^\prime=\frac{\sum_{j=1}^N \phi(Q_i)^\top \phi(K_j) V_j}{\sum_{j=1}^N \phi(Q_i)^\top \phi(K_j)}=\frac{\phi(Q_i)^\top \sum_{j=1}^N \phi(K_j) V_j^\top}{\phi(Q_i)^\top \sum_{j=1}^N \phi(K_j)}$$
- 元のSoftmax Attentionは$$V^\prime=\frac{\sum_{j=1}^N \text{sim}\left(Q_i, K_j\right) V_j}{\sum_{j=1}^N \text{sim}\left(Q_i, K_j\right)}$$の類似度関数を$$\text{sim}\left(q, k\right)=\exp\left(\frac{q^\top k}{\sqrt{D}}\right)$$とする(ただし非負)
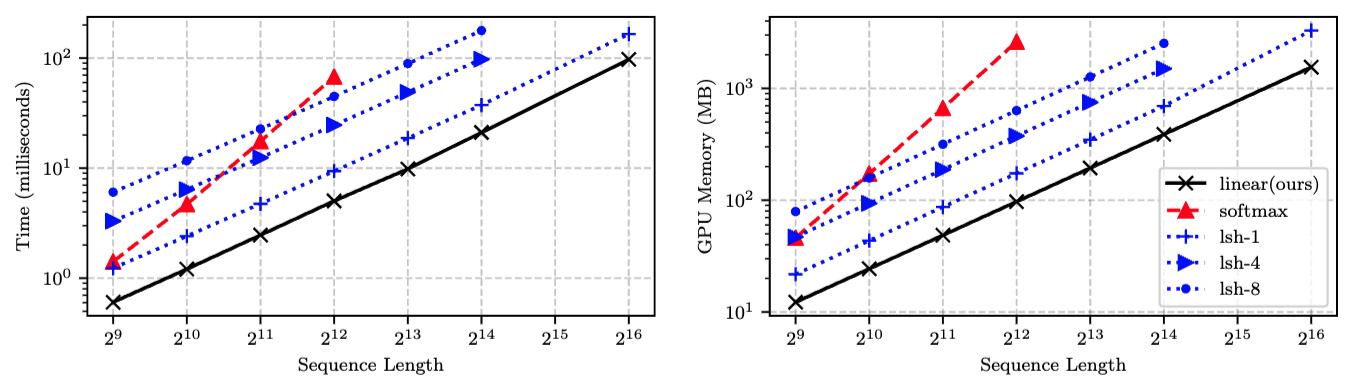
- 時間・空間ともに$O(N^2)$
- $\phi(x)\in\mathbb{R}^C$は特徴表現
- $\phi(K_j)$はクエリごとに再利用できるので計算量は時間・空間ともに$O(N)$
- ただし、指数カーネルに対応する$\phi$は無限次元なので、厳密なattentionの線形化は実行できない
- 代わりに多項式カーネルとしたときは指数カーネル・RBFカーネルと同等に機能する (tsai2019transformer) ことから、提案法では$\phi$を$$\phi(x)=\text{elu}(x)+1$$とする
- $\text{elu}$(指数線形ユニット)は$x$が負でも勾配が0にならない$$\text{elu}(x) =
\begin{cases}
x, & \text{if } x > 0 \\
\alpha \cdot (\exp(x) - 1), & \text{if } x \leq 0
\end{cases}$$
- $\text{elu}$(指数線形ユニット)は$x$が負でも勾配が0にならない$$\text{elu}(x) =
- 元のSoftmax Attentionは$$V^\prime=\frac{\sum_{j=1}^N \text{sim}\left(Q_i, K_j\right) V_j}{\sum_{j=1}^N \text{sim}\left(Q_i, K_j\right)}$$の類似度関数を$$\text{sim}\left(q, k\right)=\exp\left(\frac{q^\top k}{\sqrt{D}}\right)$$とする(ただし非負)
- 因果マスキング
- $i$番目は$j\leq i$となる$j$番目からしか影響を受けないから$$V^\prime=\frac{\sum_{j=1}^i \text{sim}\left(Q_i, K_j\right) V_j}{\sum_{j=1}^i \text{sim}\left(Q_i, K_j\right)}=\frac{\phi(Q_i)^\top \sum_{j=1}^N \phi(K_j) V_j^\top}{\phi(Q_i)^\top \sum_{j=1}^N \phi(K_j)}=\frac{\phi(Q_i)^\top S_i}{\phi(Q_i)^\top Z_i}$$となり、$S_i, Z_i$はそれぞれ$S_{i-1},Z_{i-1}$から定数時間で計算できるので、これの計算量は系列長に対して線形
- ただし$$\begin{align*}
S_i&=\sum_{j=1}^N \phi(K_j) V_j^\top\\
Z_i&=\sum_{j=1}^N \phi(K_j)
\end{align*}$$
- ただし$$\begin{align*}
- 勾配計算に必要なメモリは定数オーダー
- 学習・推論時は、$\phi(K_j)V_j^\top$行列を内部状態として保存してRNNのように時間ステップごとに更新すればよい(つまり$O(N)$)
- $i$番目は$j\leq i$となる$j$番目からしか影響を受けないから$$V^\prime=\frac{\sum_{j=1}^i \text{sim}\left(Q_i, K_j\right) V_j}{\sum_{j=1}^i \text{sim}\left(Q_i, K_j\right)}=\frac{\phi(Q_i)^\top \sum_{j=1}^N \phi(K_j) V_j^\top}{\phi(Q_i)^\top \sum_{j=1}^N \phi(K_j)}=\frac{\phi(Q_i)^\top S_i}{\phi(Q_i)^\top Z_i}$$となり、$S_i, Z_i$はそれぞれ$S_{i-1},Z_{i-1}$から定数時間で計算できるので、これの計算量は系列長に対して線形
- TransformerとRNNの関係
- Transformerの層は、前の式から、Attentionのメモリ$s$と正規化のメモリ$z$を持つRNNとして定式化できる (添え字を再帰のタイムスタンプとする)$$\begin{align*}
s_0&=0,\\
z_0&=0,\\
s_i&=s_{i-1}+\phi\left(x_iW_K\right)\left(x_iW_V\right)^\top,\\
z_i&=z_{i-1}+\phi\left(x_iW_K\right),\\
y_i&=f_l\left(\frac{\phi\left(x_iW_Q\right)^\top s_i}{\phi\left(x_iW_Q\right)^\top z_i}+x_i\right).
\end{align*}$$- 特徴関数$\phi$に制約がない
- Transformerの層は、前の式から、Attentionのメモリ$s$と正規化のメモリ$z$を持つRNNとして定式化できる (添え字を再帰のタイムスタンプとする)$$\begin{align*}
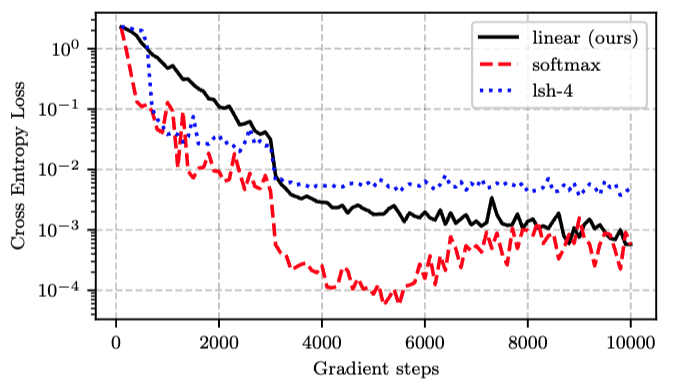
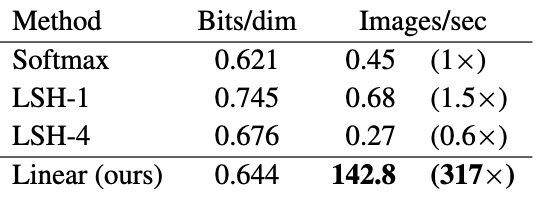
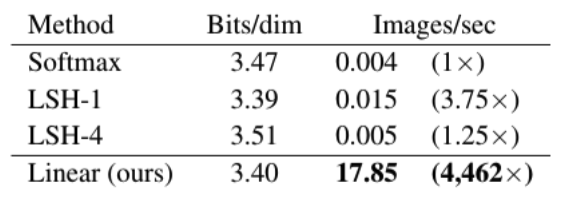
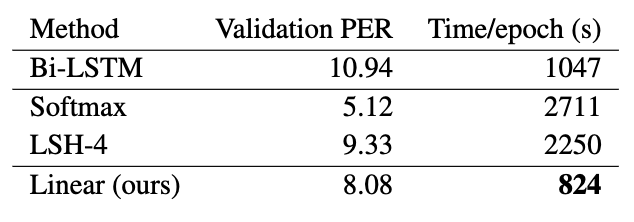
- 実験