LoginSignup
7
8

More than 1 year has passed since last update.

NTTコムウェアAdvent Calendar 2022Day 24nttcomware
@comware_tkonishi(古西 孝成)inNTTコムウェア株式会社

Jupyter上でイジングモデルのアニメーション

Last updated at Posted at 2022-12-23

この記事はNTTコムウェア Advent Calendar 2022 24日目の記事です。

NTTコムウェアの古西です。
Jupyter上で2次元イジングモデルのアニメーションを動かしてみます。また、ほんの少しだけ物理的考察を行います。

  • きっかけ
  • イジングモデルとは？
  • マルコフ連鎖モンテカルロ法とは？
  • 2次元イジングモデルのシミュレーション
  • 参考文献

きっかけ

オライリー・ジャパンの実践 時系列解析という本に、物理シミュレーションの例として、2次元イジングモデルのシミュレーションが載っています。Pythonのサンプルコードが載っているのですが、そのまま動かすと初期状態と終状態の画像のみしか表示されないため、どうせなら途中の状態をアニメーションとして表示させたい、と思ったことがきっかけです。
この本のサンプルコードはGitHub上に公開されており1、コードの一部を利用することに許可は不要との記載もあるので、こちらのコードをもとにアニメーション部分の追加を行います。また、考察のためにトレースプロット等のグラフを作成します。2。

イジングモデルとは？3

イジングモデルとは、ミクロな磁石の集合体の物理モデルです。
ミクロな磁石はそれぞれN極とS極をもちます。それぞれのミクロの磁石は、隣あった磁石が同じ向きを向きたがる性質をもっているとします。つまり、ある磁石の前後左右の磁石が全て上向きなら、その磁石も上向きを向きたがります。この性質だけだと、やがてすべての磁石が同じ向きを向きますが、磁石の向きには温度に対する依存性をもっており、磁石の温度が高くなればなるほど隣の磁石の向きに関わらず、ランダムに反転しやすい性質、つまり向きがバラバラになる性質をもってます。逆に、温度が低ければ低いほど反転しづらくなり同じ向きを向いたままになります。
初期状態は、それぞれのミクロの磁石が上向き、下向きランダムな方向を向いているとします。

ising_image.png

N極が上を向いているときを $s_i=+1$ の状態、N極が下を向いている(つまりS局が上を向いている)時の状態を$s_i=-1$と定義します。磁石の向きが揃いやすくなる概念を、ポテンシャルエネルギーの大小であらわすと、各磁石のポテンシャルエネルギー$E(s)$は、

E(s) = - \sum_{<i,j>} s_i s_j

と表すことができます。ここで、$<i,j>$は、隣接する組という意味です。
1個の磁石の前後左右4つの磁石との関係を考えるので、今見ている磁石の前後左右4つともその磁石と同じ向きを向いていると、$E(s)=-4$、2つだけ逆を向いていると$E(s)=0$、4つとも逆を向いている場合は$E(s)=+4$となります。その瞬間の磁石では、$E(s)= -4, -2, 0, +2, +4$のいずれかの値を持ちます。
ポテンシャルエネルギーは、小さい値ほど安定していることを表すので、向きが揃っているほうがエネルギー的に安定していることになります。

また、磁石の反転しやすさをあらわす確率は、既知の物理法則に従うとし4、温度(絶対温度)$T$とすると、次の確率モデルであらわせます。

P(s) = \frac{e^{-E(s)/T}}{Z}

ここで、$Z$は規格化定数5で、磁石の数が$N$個の場合

Z = \sum_{s=1}^N e^{-E(s)/T}

となります。これにより、反転のしやすさが温度に依存することもあらわせています。

ここで、この確率分布を計算しようとすると、規格化定数 $Z$を計算しないといけませんが、$N$が大きくなると、状態和の計算（一般的には積分計算）が困難になることが知られています6。これを数値シミュレーションにより近似的に求めようとするのが、今回のプログラムでも利用するマルコフ連鎖モンテカルロ法(MCMC)です。

マルコフ連鎖モンテカルロ法(MCMC)とは？7

モンテカルロ法とは、乱数を用いた数値計算手法の総称です。実際にコンピューターで数値計算する場合は、コンピューターが生成する疑似乱数を用いることになります。それでは、マルコフ連鎖とはなんでしょうか？
マルコフ連鎖とは、時点に従って脈々と変化していく確率変数があるとき、1時点前の値だけで次の確率変数がきまることを指します。つまり、

x_0 \to x_1 \to x_2 \to \dots \to x_{n-1} \to x_n

のときの状態遷移確率$P$が、

P(x_n | x_{n-1},x_{n-2}, \dots , x_1) = P(x_n|x_{n-1})

となることです。マルコフ連鎖モンテカルロ法(MCMC)は、マルコフ連鎖でできる確率変数を利用して疑似乱数を生成するモンテカルロ法のことです。では、単純なモンテカルロ法ではなく、MCMCを利用する必要性はどうしてでしょう？

一般に、多変量(高次元)の分布での計算で単純なモンテカルロ法でのサンプリングは、ほとんどの点で対象となる分布関数(被積分関数)の計算に寄与せず、生成した疑似乱数のほとんどが無駄になってしまうという問題があります。これにより、次元が高くなると、解析的な(真の意味の)解と、数値計算での近似解に大きなずれが生じることもわかっています8。今回のイジングモデルの例では、磁石の数 $N$ があまりに大きくなると利用できないことになります。
単純なモンテカルロ法が使えないということがわかったとして、MCMCの場合はなぜうまくいくのでしょうか。

MCMCでは、時間が経つにつれて、確率分布がなんらかの変化しない状態に収束する性質をもっており(つまり、時間を多少前後しても確率分布が変化しない状態)、これを定常分布と呼びます9。定常分布では、計算の対象となる分布関数に対する寄与度が高いところで重点的にサンプリングが行われるため、多変量(高次元)になっても上手く計算できるようになります。(言葉で説明してもわかりづらいので、この後のイジングモデルアニメーションの下にある定常分布のグラフをご覧ください。)

ちなみに、少し脱線しますが、MCMCの活用の場というと、イジングモデルのような物理シミュレーション以外にも、ベイズ統計モデリングの世界で使われることが多くなっています。ベイズ統計モデリングでは、ある観測データから統計モデルの仮説を立てて、事後分布の計算を行いますが、事後分布に従う疑似乱数の生成に、MCMCを利用します10。

2次元イジングモデルのシミュレーション

以下に、2次元イジングモデルのアニメーションを示します。イジングモデルの設定とMCMCの計算の関数部分は、オリジナルソースに準拠しています。
アニメーション化をするために、matplotlibのArtistAnimationモジュールを使用します。ArtistAnimationでは、あらかじめアニメーション化する画像を複数枚用意し、リストに入れておきます。今回は、各モンテカルロステップ毎に出力される状態図を配列imsに格納しています。

ising-anime.ipynb
## Original source https://github.com/PracticalTimeSeriesAnalysis/BookRepo/blob/master/Ch04/Ising.ipynb
## Modified for Animation by T.Konishi 
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from matplotlib import animation, rc
from IPython.display import HTML

### 設定
N           = 16   # 横の個数
M           = 16   # 縦の個数
T           = 1.0 # 温度 (低温)
#T            = 10.0  # 温度 (高温)
n_steps = 1500     # モンテカルロステップ数
energy = 0.0      #エネルギー値初期化
energy_n_steps = [energy] #モンテカルロステップ毎に選択されたセルのエネルギー差

plt.style.use("default") # 描画スタイルをデフォルトに設定
np.random.seed(111)  # 乱数の種を設定

# 系の初期化
def initRandState(N, M):
    block = np.random.choice([-1, 1], size = (N, M))
    return block

# エネルギー差の計算
def energyForCenterState(state, i, j, n, m):
    centerS = state[i, j]
    neighbors = [((i + 1) % n, j), ((i - 1) % n, j),
                 (i, (j + 1) % m), (i, (j - 1) % m)]
    ## 周期的な境界条件のために %n としている。

    interactionE = [state[x, y] * centerS for (x, y) in neighbors]
    return np.sum(interactionE)

def magnetizationForState(state):
    return np.sum(state)

# MCMCの計算
def mcmcAdjust(state):
    n = state.shape[0]
    m = state.shape[1]
    x, y = np.random.randint(0, n), np.random.randint(0, m)
    centerS = state[x, y]
    energy = energyForCenterState(state, x, y, n, m)
    if energy < 0:
        centerS *= -1
    elif np.random.random() < np.exp(-energy / T):
        centerS *= -1
    state[x, y] = centerS
    return state, energy

fig = plt.figure(figsize=(5,5)) # 図のサイズ
ims=[]
state = initRandState(N, M)
magnet_hist = []
    
for i in range(n_steps):
    state, energy = mcmcAdjust(state)
    energy_n_steps.append(energy) 
    magnet_hist.append(magnetizationForState(state))
    im = plt.imshow(state, animated=True)
    ims.append([im])

# アニメーション
anim = animation.ArtistAnimation(fig, ims, interval=10)
rc('animation', html='jshtml')
plt.close()
anim

#動画gifファイルの保存
anim.save("ising_temp_low.gif")
#anim.save("ising_temp_high.gif")

plt.style.use("ggplot") #グラフ描画用にスタイル変更

df = pd.DataFrame(energy_n_steps)

# モンテカルロステップ毎に算出するエネルギー値のトレースプロット
plt.figure(figsize=[5, 3])
plt.plot(df[0])
plt.xlabel("n_steps")
plt.ylabel("energy")
plt.tight_layout()
plt.savefig("./energy_trace_plot_low.png")
plt.show()

# 算出されたエネルギー値のヒストグラム
plt.figure(figsize=[5, 3])
plt.hist(df[0], align='mid', density = False, bins = 5, range = (-5, 5), rwidth=0.5)
plt.xlabel("energy")
plt.ylabel("count")
plt.tight_layout()
plt.savefig("./energy_histgram_low.png")
plt.show()
  • ArtistAnimationの見た目と、シミュレーションの初期状態
    artistanimation_init.png

MCMCの計算部分がミソです。11

  • 各モンテカルロステップ毎に、1つのセル(ミクロな磁石をここではセルと呼ぶことにします。)を選び、その向きを反転させる。
  • 反転した結果、変化したエネルギー差を計算する。
    • エネルギー差が0より小さい場合、常に優先される低いエネルギー状態にへの遷移を意味するため、反転を受け入れて次に進む。
    • エネルギー差が0以上であれば、$0 ～ 1$の一様乱数を生成し12、$ e^{E / T}$ ($E$はエネルギー差) と比較して生成した乱数が小さければ、反転を受け入れて次に進む。
  • 上記手順を状態が収束するまで繰り返す。

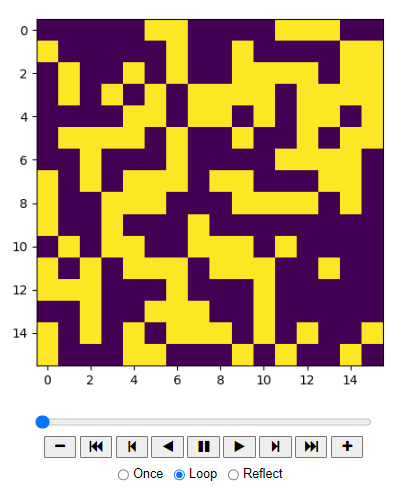
温度が低い時$(T=1.0)$と、温度が高い時$(T=10)$のシミュレーション結果のアニメーションは以下のようになります。
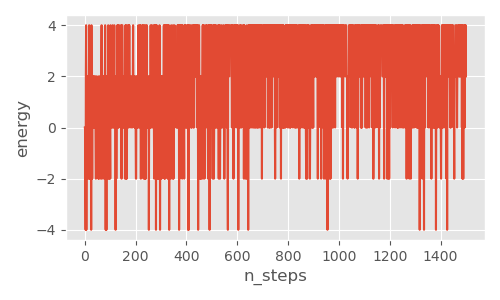
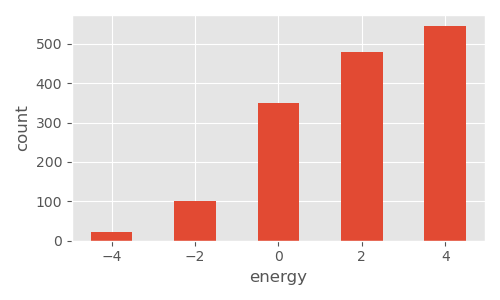
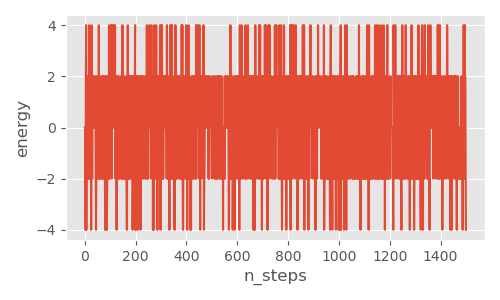
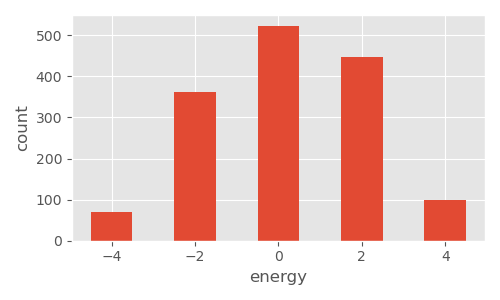
温度が低いときは、時間が進むにつれて磁石の向きが揃って島状の塊ができますが、温度が高いときは、バラバラのままです。また、温度が低い時、高い時に計算されるエネルギー差の推移を示すトレースプロットと、ヒストグラム13をあわせて載せておきます。温度が低い時は、各セルを反転させた際にエネルギー差が大きくなりがちで、かつ反転させる確率も低くなるため、セルの向きはそろう方向となり、状態が収束します。トレースプロットをみても、時間に寄らない定常分布になっていることがわかります。また、温度が高い時は、逆にエネルギー差が$0$付近を中心に均等になり、定常分布となります。

  • 温度が低い時$(T=1.0)$
    ising_temp_low.gif
    energy_trace_plot_low.png
    energy_histgram_low.png

  • 温度が高い時$(T=10.0)$
    ising_temp_high.gif
    energy_trace_plot_high.png
    energy_histgram_high.png

温度が低いときはセルの向きが揃おうとするのに対し、温度が高い時はセルの向きがバラバラのままになりますが、それでは、その境界となる温度はどこになるでしょうか？
実は、今回のような正方格子型の2次元イジングモデルでは、$T=$2.27付近のところがその境界になることが分かっています(と、これならわかる機械学習入門に書いてあるので14、その受け売りです)。このように、ある温度で状態が変化することを物理の世界では相転移と言います。今回は、簡易なモデルとシミュレーションにより、2次元イジングモデルの相転移について様子を見てみました。

参考文献

  • 実践 時系列解析 統計と機械学習による予測(Aileen Nielsen 著、山崎 邦子、山崎 康宏 訳、オライリー・ジャパン) ISBN: 978-4-87311-960-1
    • タイトルのとおり、時系列解析の本です。RとPythonのサンプルコードが豊富です。今回は、この本の内容とサンプルコードをきっかけに記事を書きましたが、この本自体では、イジングモデルもMCMCを2～3ページに触れられているのみです。ただし、時系列解析の概観、前処理、統計モデル、適用事例等を知るためには良い本だと思います。
  • ゼロからできるMCMC　マルコフ連鎖モンテカルロ法の実践的入門 (花田政範／松浦壮・著) ISBN: 978-4-06-520174-9
    • MCMCについては、ベイズ統計の本にモデリング手法として紹介されていることが多いのですが、この本は逆でモンテカルロ法の説明からはじまって一冊丸ごとMCMCに関して記述されていて、ベイズ統計やイジングモデル等の物理学への応用はその適用例として出てきます。この本に載っているサンプルコードはCおよびC++で一見とっつきにくいのですが、説明が丁寧なのと、サンプルコードが掲載されているGithub上にはC、C++のコードに加えてPythonでのサンプルコードも掲載されています。
  • これならわかる機械学習入門 (富谷昭夫・著) ISBN: 978-4-06-522549-3
    • 著者が物理学が専門なので、物理学寄りの機械学習入門です。一章まるごとイジングモデルに割かれており、記述も詳しいです。ただ、タイトルの「これならわかる」は多少疑問があり、機械学習と物理学に関して全く知見がないと読み進めるのは難しいと思います。逆に知っていると「くすっ」とするところが多々あります。

これ以外にも、イジングモデルであれば統計力学の教科書、MCMCであれば機械学習やベイズ統計の教科書等良い専門書が多くあります。統計力学、ベイズ統計ともに数式が多用されどうしても忌避してしまうところがありますが15、理解ができると深淵な世界が広がっています。また、最近は画像処理等に統計力学的な手法が使われる等、情報と物理の両方の境界領域のような分野もあります16。少しでも興味があるところから、書店で読めそうな本を手に取って一歩進めていただけたらと思います。

※ 文中に記載されている会社名、商品名、製品名は各社の商標または登録商標です。

  1. https://github.com/PracticalTimeSeriesAnalysis/BookRepo/blob/master/Ch04/Ising.ipynb ↩

  2. オリジナルのソースコードとは、一部記事の内容に合わせて変数名を変えています。 ↩

  3. 厳密な説明は私の手に余るので、この記事ではざっくりとした説明しかしません。一般向けの平易な解説としては、こちらのenakai00さんのブログ記事が分かりやすくてよいと思います。なお、本記事について明らかな間違いを見つけた時は、ご指摘ください。 ↩

  4. 物理学(統計力学)でいうボルツマン分布です。 ↩

  5. 統計力学の世界では分配関数と呼ばれます。 ↩

  6. うそおっしゃい。この記事のプログラムの例$(N=16 \times 16)$ぐらいだったらすぐに計算できるだろ、とつっこまないでください。一般論を言っています。 ↩

  7. Markov chain Monte Carlo、略してMCMCです。 ↩

  8. 次元の呪いと呼ばれています。 ↩

  9. MCMCで定常分布を作る手法には、メトロポリス法、ギプス・サンプラー(熱浴法)、ハミルトニアンモンテカルロ法等、いくつかあります。 ↩

  10. 私自身、現在はAIやデータサイエンス関連の仕事をしていますが、実はまだ直接MCMCが必要になる仕事に出会ったことがありません。どこにあるのでしょうか。ちなみに、ベイズ的なアプローチ自体にはちょっと仕事で出会いました。 ↩

  11. これがメトロポリス法です。 ↩

  12. 元となったソースファイルで、0以上1未満の一様乱数の生成にnumpy.random.randomが使ってあって最初見たときに「np.random.randomってなに？np.random.randじゃないの？」と思ってnumpy.random.randのマニュアルページをみると、This is a convenience function for users porting code from Matlab, and wraps random_sample.と書いてあってrandom.randomはrandom.random_sampleのエイリアスなので、結局はrandom.randはrando.random_sampleをラップしていると認識しました。random_sampleのマニュアルページには、random.Generator.random which should be used for new code.といったことも書いてありますが、今回は元ソースのままrandom.randomを使っています。 ↩

  13. このヒストグラムを最初正規化(モンテカルロステップ数で割って確率密度のグラフにする)しようとして、plt.histのdensityオプションをTrueにしてみたのですが、なぜか全体の和が1.0にならず見た目にもおかしな値のグラフになるので今回の掲載では一旦あきらめました。後で、matplotlib.pyplot.histのマニュアルページのdensityオプションのところに「If True, draw and return a probability density: each bin will display the bin's raw count divided by the total number of counts and the bin width (density = counts / (sum(counts) * np.diff(bins))),」と書いてあるのに気がつき、割る数が各binのカウント数$\times$bin幅(今回の場合、bin幅が2なので、モンテカルロステップ数1500$\times$2=3000)になってしまうと理解しました。範囲とbin数の調整をすればいけそうな気がします。 ↩

  14. 正確には逆温度($=1/T$)が0.440$\dots$と書いてあるのですが、この記事の本文では逆温度をいう言葉を使っていないので逆数を取っています。 ↩

  15. 私自身、数式がいっぱいあると読めません。苦手意識を克服するだけの好奇心と情熱がいります。 ↩

  16. ベイズ統計の有名な本にベイズ統計の理論と方法 (渡辺澄夫著、コロナ社)という本がありますが、書店で最初手に取ったとき3ページ目に「逆温度」、4ページ目に「分配関数」という言葉が出てきて、「統計力学知らないとこの本読めないじゃん(まだまだ読めないな)」と思ってそっと元の書棚に戻しました。 ↩

7
8
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
7
8