Flux.jlで量子力学

面白そうなプレプリントA simple method for multi-body wave function of ground and low-lying excited states using deep neural networkがありましたので、最初の部分をFlux.jlで再現してみようと思います。

最初の部分の概要

1次元1粒子の量子力学を考えます。

H \psi(x) = E \psi(x) \\
H = -\frac{1}{2} \frac{d^2}{dx^2} + V_{\rm ext}(x) \\

この固有値問題の最小固有値とその時の波動関数が欲しい、という問題です。論文では2粒子以上のこともやっていますが、ここではJuliaの機械学習フレームワークであるFlux.jlの練習として、1粒子だけをやってみます。
ここで$x$は連続的な変数ですが、数値計算では$x$を離散的にします。つまり、$ x_j = -x_{\rm max} + hj$, $h = 2 x_{\rm max}/M$とします。ここで、$M$は刻み数で、$x_j$は$M-1$個あるとします。そして、$\psi(x)$は$\psi_j = \psi(x_j)$という離散点で評価されているとします。この時、2階微分は差分化されます。ポテンシャル$V_{\rm ext}(x)$は

V_{\rm max}(x) = \frac{1}{2} \omega^2 x^2

という調和振動子型ポテンシャルとします。細かいところは元のプレプリントを参照してください。

このハミルトニアンに対する固有関数$\psi(x)$をニューラルネットワークで見つける、という話です。論文中では2粒子や3粒子、フェルミオンやボソンの場合についてやっています。フェルミオンやボソンの場合、波動関数に入れ替えに対する条件がかかるのですが、それをどのように考慮するか、などについて書かれています。

通常のやり方のコード

まず、ハミルトニアンを作成します。まず、2階微分とポテンシャルに対応する行列を作成するコードは

using SparseArrays
using LinearAlgebra
function make_T(M)
    T = spzeros(Float64,M-1,M-1)
    for i=1:M-1
        j = i -1
        if 1 <= j <= M-1
            T[i,j] = 1
        end
        j = i + 1
        if 1 <= j <= M-1
            T[i,j] = 1
        end
        T[i,i] = -2
    end
    return T
end

function make_V(M,ω,xs)
    V = spzeros(Float64,M-1,M-1)
    for i=1:M-1
        x = xs[i]
        V[i,i] = (1/2)*ω^2*x^2
    end
    return V
end

です。
ハミルトニアン行列$H$がわかれば固有値問題を解けば最低エネルギーは求まりますので、

function test()
    M = 2048
    xs = zeros(Float64,M-1)
    xmax = 5
    h = 2*xmax/M
    for j=1:M-1
        xs[j] = -xmax + h*j
    end
    T = make_T(M)
    ω = 1
    V = make_V(M,ω,xs)
    H = -T ./(2h^2) + V

    e_eigen,v = eigen(Matrix(H))
    groundstate_energy = e_eigen[1]
    println("最低エネルギー ",groundstate_energy)
end
test()

とすればよいです。結果は、

最低エネルギー 0.49999925501515124

です。厳密解では0.5になるそうですので、$M = 2048$と離散化している影響は出ているようですが、悪くなさそうです。

ニューラルネットワークによる基底エネルギー探索

次に、エネルギーが最小になるような波動関数をニューラルネットワークで探索してみます。つまり、

\psi(x) = f(x)

という形で、関数$f$をニューラルネットワークで作成します。インプットは$x$座標、アウトプットは波動関数$\psi(x)$です。
Flux.jlでやる場合には、

using Flux
n1 = 4
model = Chain(x -> [x],Dense(1,n1,Flux.softplus),Dense(n1,1,Flux.softplus),x -> sum(x)) |> Flux.f64
println(model(0.2))

のようにすれば全結合ニューラルネットワークが作れます。論文と同じように活性化関数としてsoftplusを用いました。これは隠れ層一層です。Chainの最初のx -> [x]は一つのスカラーを1成分の配列にしているところです。最後のx -> sum(x)は逆に1成分の配列として出てくるものをスカラーにしているものです。最後の|> Flux.f64は、デフォルトだとモデルが単精度のパラメータなので、それを倍精度Float64のパラメータに変換しています。

このニューラルネットワークに対して、loss関数を定義します。今、最低エネルギーが計算したいわけですが、エネルギーは

E = \frac{\vec{\psi}^T H \vec{\psi}}{\vec{\psi}^T \vec{\psi}}

で求まります。ですので、これをloss関数とします。つまり、

function energy(model,xs)
    ψ = model.(xs)
    c = ψ'*ψ
    E = ψ'*H*ψ/c
    return E
end 

です。
あとはトレーニングするだけです。これは

opt = Flux.setup(Adam(), model)
lossdata = Float64[]
for i=1:50000
    Flux.train!(energy, model,(xs,), opt)
    e = energy(model,xs)
    loss = e- groundstate_energy 
    push!(lossdata,loss)
    if i % 1000  == 0
        println("i = $i energy = $e, loss = $loss")
    end
end


plot(lossdata,yscale=:log10)
savefig("lossdata.png")

みたいな感じでできます。
全体のコードは

using Plots
using Flux
using SparseArrays
using LinearAlgebra

function make_T(M)
    T = spzeros(Float64,M-1,M-1)
    for i=1:M-1
        j = i -1
        if 1 <= j <= M-1
            T[i,j] = 1
        end
        j = i + 1
        if 1 <= j <= M-1
            T[i,j] = 1
        end
        T[i,i] = -2
    end
    return T
end

function make_V(M,ω,xs)
    V = spzeros(Float64,M-1,M-1)
    for i=1:M-1
        x = xs[i]
        V[i,i] = (1/2)*ω^2*x^2
    end
    return V
end


function test()
    M = 2048
    xs = zeros(Float64,M-1)
    xmax = 5
    h = 2*xmax/M
    for j=1:M-1
        xs[j] = -xmax + h*j
    end
    T = make_T(M)
    ω = 1
    V = make_V(M,ω,xs)
    H = -T ./(2h^2) + V

    e_eigen,v = eigen(Matrix(H))
    groundstate_energy = e_eigen[1]
    println("最低エネルギー ",groundstate_energy)

    n1 = 4
    model = Chain(x -> [x],Dense(1,n1,Flux.softplus),Dense(n1,1,Flux.softplus),x -> sum(x)) |> Flux.f64
    println(model(0.2))

    function energy(model,xs)
        ψ = model.(xs)
        c = ψ'*ψ
        E = ψ'*H*ψ/c
        return E
    end 

    println(energy(model,xs))

    
    opt = Flux.setup(Adam(), model)
    lossdata = Float64[]
    for i=1:50000
        Flux.train!(energy, model,(xs,), opt)
        e = energy(model,xs)
        loss = e- groundstate_energy 
        push!(lossdata,loss)
        if i % 1000  == 0
            println("i = $i energy = $e, loss = $loss")
        end
    end

    plot(lossdata,yscale=:log10)
    savefig("lossdata.png")

end
test()

です。出力の一部は

i = 43000 energy = 0.49999939608132177, loss = 1.4106617052256354e-7
i = 44000 energy = 0.499999391177304, loss = 1.3616215277512111e-7
i = 45000 energy = 0.49999938654050446, loss = 1.3152535321969694e-7
i = 46000 energy = 0.4999993821287106, loss = 1.2711355934502677e-7
i = 47000 energy = 0.4999993779289742, loss = 1.2291382295304132e-7
i = 48000 energy = 0.4999993764870648, loss = 1.2147191352784859e-7
i = 49000 energy = 0.49999937023602253, loss = 1.1522087128845726e-7
i = 50000 energy = 0.4999993666713795, loss = 1.1165622826325716e-7

みたいな感じになっています。数値計算での最低エネルギーが

最低エネルギー 0.49999925501515124

でしたので、これに近づいていっていることがわかります。
lossのグラフは

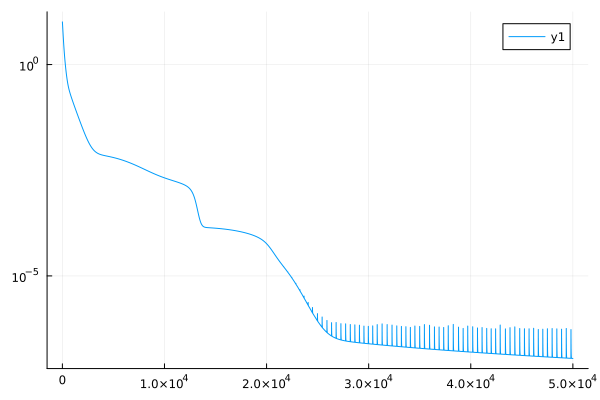
のような感じです。ユニット数がたったの4にもかかわらずかなりいい感じになっています。