ある三次元の配列があるとします。つまり、x,y,zを指定すると一つの値f(x,y,z)があるような状況です。この時、fがある値となるような点の集合を描きたいとします。
これは固体物理学では「フェルミ面を描く」ことに対応しています。Juliaの色々なライブラリを使うことでできることがわかりましたので、記録として残しておきます。
バージョン
Julia 1.8.1
インストール
必要なパッケージは以下の通りです。addでインストールしてください。
- Interpolations
- Meshing
- FileIO
- MeshIO
- GeometryBasics
サンプルデータの生成
サンプルデータとして、
E(k_x,k_y,k_z) = -(\cos(k_x) + \cos(k_y) + \cos(k_z))
とします。この関数がゼロとなるような点の集合を集めると、面になります。固体物理学ではこれはフェルミ面と呼ばれるものです。
この関数は解析的な形で求まっていますが、一般には数値的な値しかないかもしれません。そこで、この関数から適当に生成したサンプルデータを作成します。
using Interpolations
using Meshing
using FileIO #MeshIOもインストールしないといけない
using GeometryBasics
using LinearAlgebra
function make_data(nkx,nky,nkz)
kxs = range(-pi,pi,length=nkx)
kys = range(-pi,pi,length=nky)
kzs = range(-pi,pi,length=nkz)
energy= zeros(Float64,nkx,nky,nkz)
for iz=1:nkz
kz = kzs[iz]
for iy=1:nky
ky = kys[iy]
for ix=1:nkx
kx = kxs[ix]
energy[ix,iy,iz] = -(cos(kx) + cos(ky) + cos(kz))
end
end
end
return energy
end
データの補間
次に、メッシュで切ったデータ点以外の値を計算できるようにするために、スプライン補間のパッケージInterpolationsを用います。
function energy_dispersion(energymesh)
nka,nkb,nkc = size(energymesh)
kas = range(0,2pi,length=nka)
kbs = range(0,2pi,length=nkb)
kcs = range(0,2pi,length=nkc)
interp_cubic = cubic_spline_interpolation((kas, kbs,kcs), energymesh)
function evaluate(ks)
#println(typeof(ks))
vecka = [ks[1],ks[2],ks[3]]
for i=1:3
while vecka[i] < 0
vecka[i] += 2pi
end
while vecka[i] > 2pi
vecka[i] -= 2pi
end
end
#println(vecka)
return interp_cubic(vecka...)
end
return ks -> evaluate(ks),interp_cubic
end
この関数は、データのメッシュをもらうと、関数evaluate(ks)と補間用データを返してくれます。
ですので、
nkx = 21
nky = 21
nkz = 21
energy_mesh = make_data(nkx,nky,nkz)
evaluate,interp_cubic = energy_dispersion(energy_mesh)
のようにすると、データのメッシュを21x21x21で作成した後に、補間用の関数evaluateを作成したことになります。
ポリゴンデータの作成
最後に、ポリゴンを作成します。これは、
function main()
nkx = 21
nky = 21
nkz = 21
energy_mesh = make_data(nkx,nky,nkz)
evaluate,interp_cubic = energy_dispersion(energy_mesh)
μ = 0.0
println(evaluate([0.2,0.1,0.3]))
km = pi
cosmesh = Mesh(evaluate, Rect(Vec(-km,-km,-km),Vec(2km,2km,2km)),
MarchingCubes(iso=-μ), samples=(50,50,50))
save("cos.ply", cosmesh)
a = zeros(Float64,3)
b = zero(a)
c = zero(a)
g = zero(a)
fp = open("fermi.txt","w")
for tri in cosmesh
kcount = 0
for r in tri
kcount += 1
if kcount == 1
a[:] = r[:]
elseif kcount == 2
b[:] = r[:]
else
c[:] = r[:]
end
end
g[:] = (a+b+c)/3 #三角形の中心座標
a[:] = a-c
b[:] = b-c
if norm(a-b) < 1e-10
continue
end
s = sqrt(norm(a)^2*norm(b)^2 - dot(a,b)^2)/2 #三角形の面積
println(fp,g[1],"\t",g[2],"\t",g[3],"\t",s)
end
close(fp)
end
main()
で可能です。
ここで、
km = pi
cosmesh = Mesh(evaluate, Rect(Vec(-km,-km,-km),Vec(2km,2km,2km)),
MarchingCubes(iso=-μ), samples=(50,50,50))
がポリゴンデータを作成しているところです。Rect(Vec(-km,-km,-km),Vec(2km,2km,2km))は、始点が(-km,-km,-km)で、そこからベクトル(2km,2km,2km)を足した点を対角線の点とした時の直方体領域を指定しています。
このデータは
save("cos.ply", cosmesh)
でply形式で保存ができます。ply形式は、MeshLabなどで読み込むことができます。
例えば、

こんな感じです。
また、Makie.jlも対応していますので、綺麗なプロットを描くこともできます。
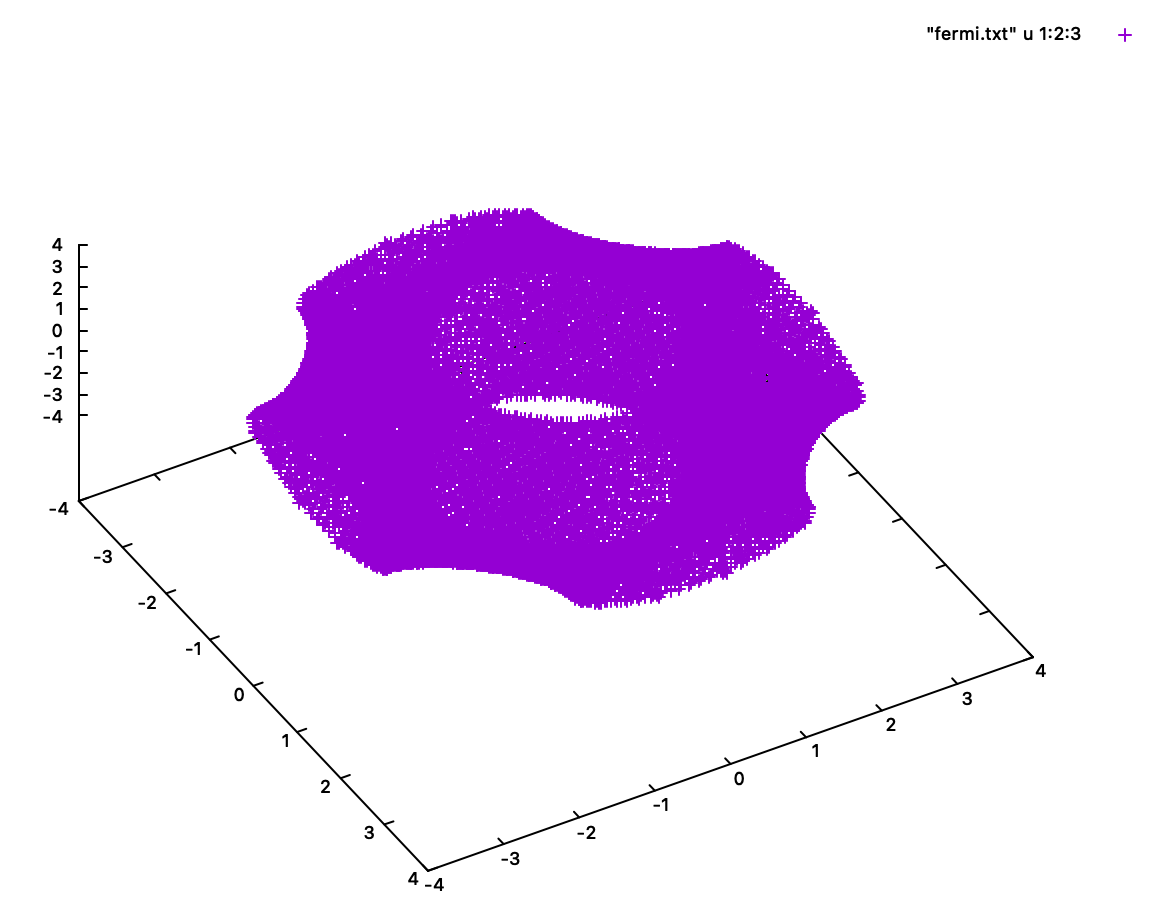
サンプルコードではデータとして書き出していますから、gnuplotなどでもプロット可能で、この場合には、
みたいにプロットできます。
コードではポリゴンを構成する三角形の面積を求めて、それもファイルに書き出しています。これは、表面積分を行うときの面積素として使うことができますから、表面積の計算や表面での何らかの量の計算が可能となります。