コード
https://gist.github.com/comefrombottom/3a4696983ae6fb73e265011ebdde5be1
📃
動作
変数の意味
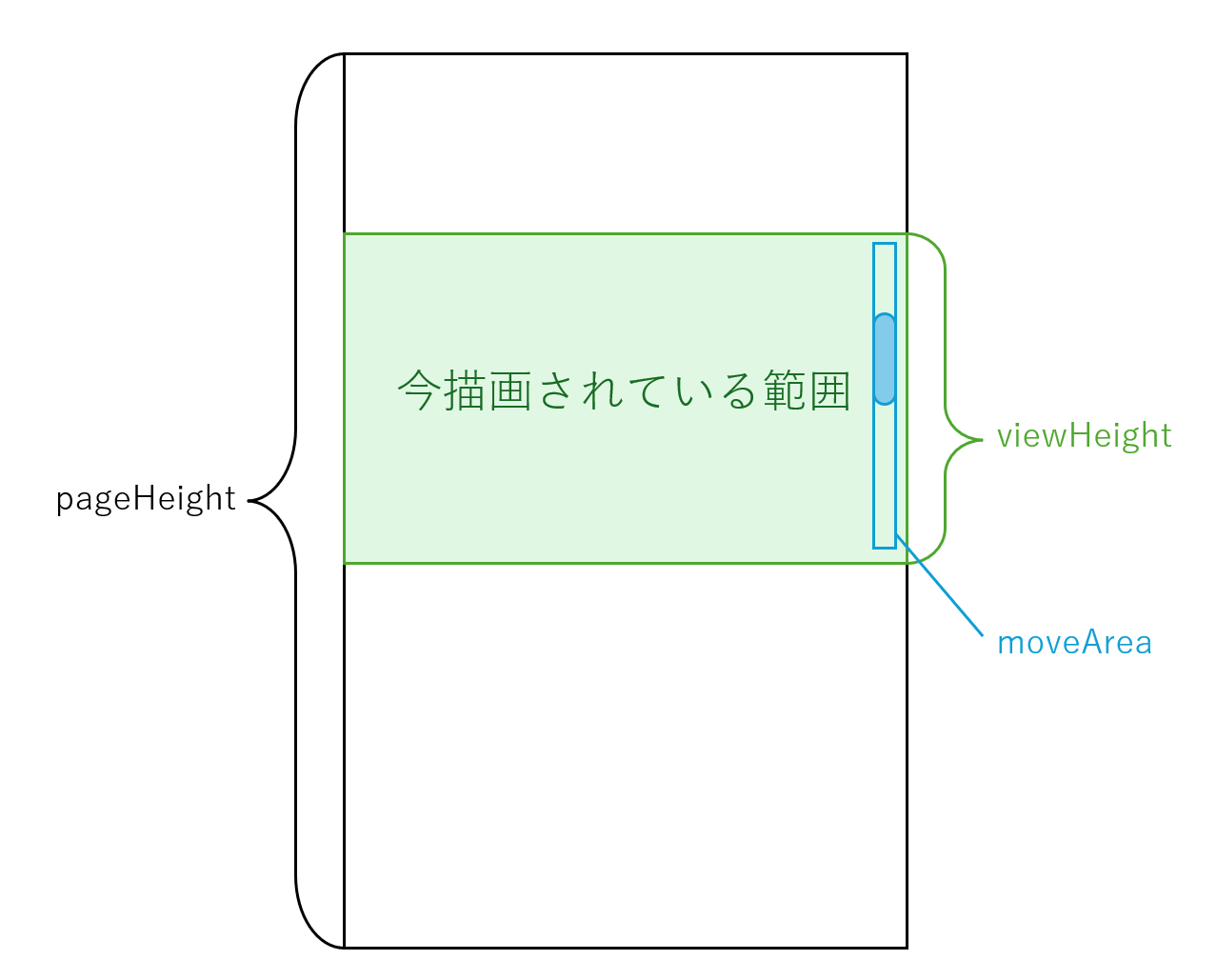
コンストラクタ引数はそれぞれこの図のような意味があります。
中身のちょっと非自明なところを解説
.scroll✕✕✕To()や.scrollBy()、.scrollAdd()によって好きな座標分移動させることができますが、中身はただスクロールバーの速度を変えているだけです。
.scrollBy()は速度を指定し、.scrollAdd()速度を加算します。
素早く二回連続で呼んだときにちゃんと二回分進んでほしい場合は.scrollAdd()を使います。
つまり、.scrollBy(100)は描画場所を丁度100進めたところでピッタリ止まってくれるような速度を算出して速度に代入しているわけです。
スクロールバーはどのような挙動をしているかというと、
座標の更新:
viewTop += viewVelocity * stepTime;
速度の更新:
viewVelocity += -viewVelocity * stepTime * resistance;
に従って減速しながらviewTopをずらしていきます。
$T$ : viewTop , $V$ : viewVelocity , $S$ : stepTime , $R$ : resistance
と表します。
$$\alpha = 1 - RS$$
とすると、速度は$V→V\alpha→V\alpha^2→V\alpha^3→…$と減速していきます。
よって位置は、
$$ΔT=VS+V\alpha S+V\alpha^2 S +V\alpha^3 S +…$$
で計算でき、無限等比級数の和であることが分かります。
$$ΔT=VS+VS\alpha+VS\alpha^2 +VS\alpha^3 +…$$
$$\alpha ΔT=VS\alpha+VS\alpha^2 +VS\alpha^3 +…$$
$$(1-\alpha)ΔT=VS$$
$\alpha = 1 - RS$を代入し、
$$RSΔT=VS$$
$$V=RΔT$$
$ΔT$動かすための$V$を求めることができました。なんと$S$が消えてとてもシンプルな式になりました!
コードを見てみましょう。
void scrollBy(double h) {
viewVelocity = resistance * h;
}
なんとこれだけでhだけスクロールさせる処理になっています。驚きですね。
正直何か目標座標的なメンバ変数を持たせて追従モードみたいなものを実装した方が色々自由に制御できそうですが、こんなに簡潔に表現できるならこの方式を採用せざるを得ませんね。
以上