量子計算アニーリングマシン
量子計算の研究をなさっている先生の研究室で、少し学んでいます。![]()
アニーリングとは、最適解の探索を行う汎用アルゴリズムです。![]()
量子アニーリング方式を用いて、組合せ最適化問題を解いてくれるのが量子コンピュータ、つまり量子アニーリングマシン。
量子コンピュータの方式には「量子アニーリング方式」と「量子ゲート方式」の二つがあります。
現実性から行くと、前者は従来の計算機と量子コンピュータのハイブリッドのようなもので現実味があるそうです。つまり、大人の事情に合わせて、妥協もできるとのこと。![]() それも大事ですよね。
それも大事ですよね。
後者の量子ゲート方式は、夢のコンピュータと呼ばれ、従来の計算機に比べて高速に難解な計算を解いてしまうというものです。最近、Googleが研究の成功を発表して話題になりましたね!!
これに関しては様々な反響があるようですが…
こんなご時勢ですし、課題が結構面白かったので、書き留めておきます![]()
余談ですが、先日、情報系の研究をしている方と、量子コンピュータの将来性について話し合いました。
「本体がめちゃくちゃ大きくて、集積回路の小型化は頭打ちだから、普及は現実的じゃないよね~」
Googleの発表への反響を含め、いろんな意見がありますね、どうなるのか。
有用な活用先が見つかれば、予算もついて研究も進んで、、!
とかいう可能性があるので、その一助になりますように。
そんな意味も込めてこの記事をお届けします。
可能性は潰したくないよね![]()
日本地図の塗り絵
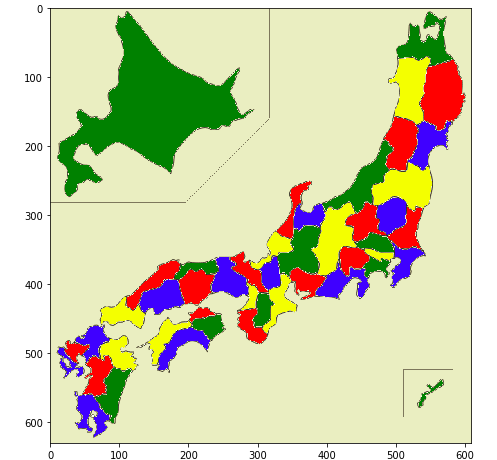
隣接する都道府県を違う色で塗るという制約を与えて、コンピュータに日本地図の塗り分けを頼んでみた。
今回、この問題をアニーリングマシンで解ける形でプログラムしよう!という話です。
アニーリングマシンが解ける形に式変形する
この記事を読んでくださる皆さんが、いつ赤ちゃんに
![]() 「この制約条件で塗り絵を秒殺して」
「この制約条件で塗り絵を秒殺して」
って言われてもいいように、コードを貼ります。
マシンの多くが入力として持つ、QUBO形式(イジング模型)に変換して実行ます。
数式に関しては、冗長になりそうなので割愛しますが、興味があればコメントください。
考え方としては、隣り合う都道府県に同じ色を割り当てたら、ペナルティでエネルギーが減点されて、最終的なエネルギーが-47(焼きなまし法なので、成功ならば負の値になる)にならなければ、塗り分け失敗という判断が下される、というものです。(条件分岐コードによって判断)
実行環境は、googleのcolaboratoryです。クラウドで実行される、jupiter notebook環境です。
まずパッケージをインストール。
# 地図を描くためのパッケージ
!pip install japanmap
# イジング模型およびQUBO形式の問題を解くためのパッケージ
!pip install dimod
次に、必要なパッケージを読み込む。今回は日本地図のデータを。
# 地図を描くためのパッケージ
from japanmap import *
# イジング模型およびQUBO形式の問題を解くためのパッケージ
import dimod
# NumPy
import numpy as np
# 図の描画の関係パッケージ
%matplotlib inline
import matplotlib.pyplot as plt
from pylab import rcParams
次のコードが数式の部分です。
def Hamiltonian(q, alpha = 1.0):
"""ハミルトニアンを計算してQUBO形式で返す
q: 色の数
alpha: 制約の強さ
"""
A = np.zeros((47*q, 47*q)) # 47都道府県をq色でぬる
# 第1項:問題を表す
for i in range(1, 48): # 各都道府県について
for j in adjacent(i): # iに隣接する県jについて
for a in range(q): # 各県にq色準備
k1 = q*(i - 1) + a
k2 = q*(j - 1) + a
A[k1, k2] += 1
# 第2項:制約条件
for i in range(47):
for a in range(q):
k1 = q*i + a
for b in range(q):
k2 = q*i + b
if k1 == k2: # 1次の項は対角成分に入れる
A[k1, k2] -= alpha
else:
A[k1, k2] += alpha
# dimodソルバー用のQUBO形式に変換
Q = {}
for k1 in range(47*q):
for k2 in range(47*q):
if A[k1, k2] != 0:
Q[(k1, k2)] = A[k1, k2]
return Q
コメントアウトに書いてあるように、qは塗り分ける色の数なので、この変数に入れる数字を変えるだけで色数を変更できます。色々試してみてください。まずは4色でやってみましょう。
q = 4 # 色の数を設定
# ハミルトニアンのQUBO形式
Q = Hamiltonian(q)
# ソルバーの設定:シミュレーテッド・アニーリング
solver = dimod.SimulatedAnnealingSampler()
# ソルバーによる求解
response = solver.sample_qubo(Q)
# 解とエネルギーを取り出す
sample0, energy0 = next(response.data(fields=['sample', 'energy']))
# 計算結果の判定
if energy0 == -47:
print('ぬりわけ成功!')
else:
print('ぬりわけ失敗')
「ぬりわけ成功!」と表示されました!!![]()
やっぱり視覚化させていので、塗り絵の結果を表示させてみましょう。
colors = {i: 'white' for i in range(1, 48)} # 色を白に初期化
# 都道府県ID(i)と色(a)を解の情報からとりだす
for key, val in sample0.items():
i = key // q + 1
a = key % q
# 色の割り当て
if val == 1:
colors[i] = ['yellow', 'blue', 'green', 'red'][a]
# 図のサイズを指定してプロットする
rcParams['figure.figsize'] = 8,8
plt.imshow(picture(colors))
まとめ
いかがでしたでしょうか?
この課題は、組合せ最適化問題の良い例だと思います。
商用化される目的としては、薬の開発の際に行う成分の組み合わせの計算を高速に終わらせることができる、などとても便利で有用な目的が数多くあります。
今後どう利用されていくか、注目ですね!![]()