（十二面のサイコロとか作れるかも）
はじめに
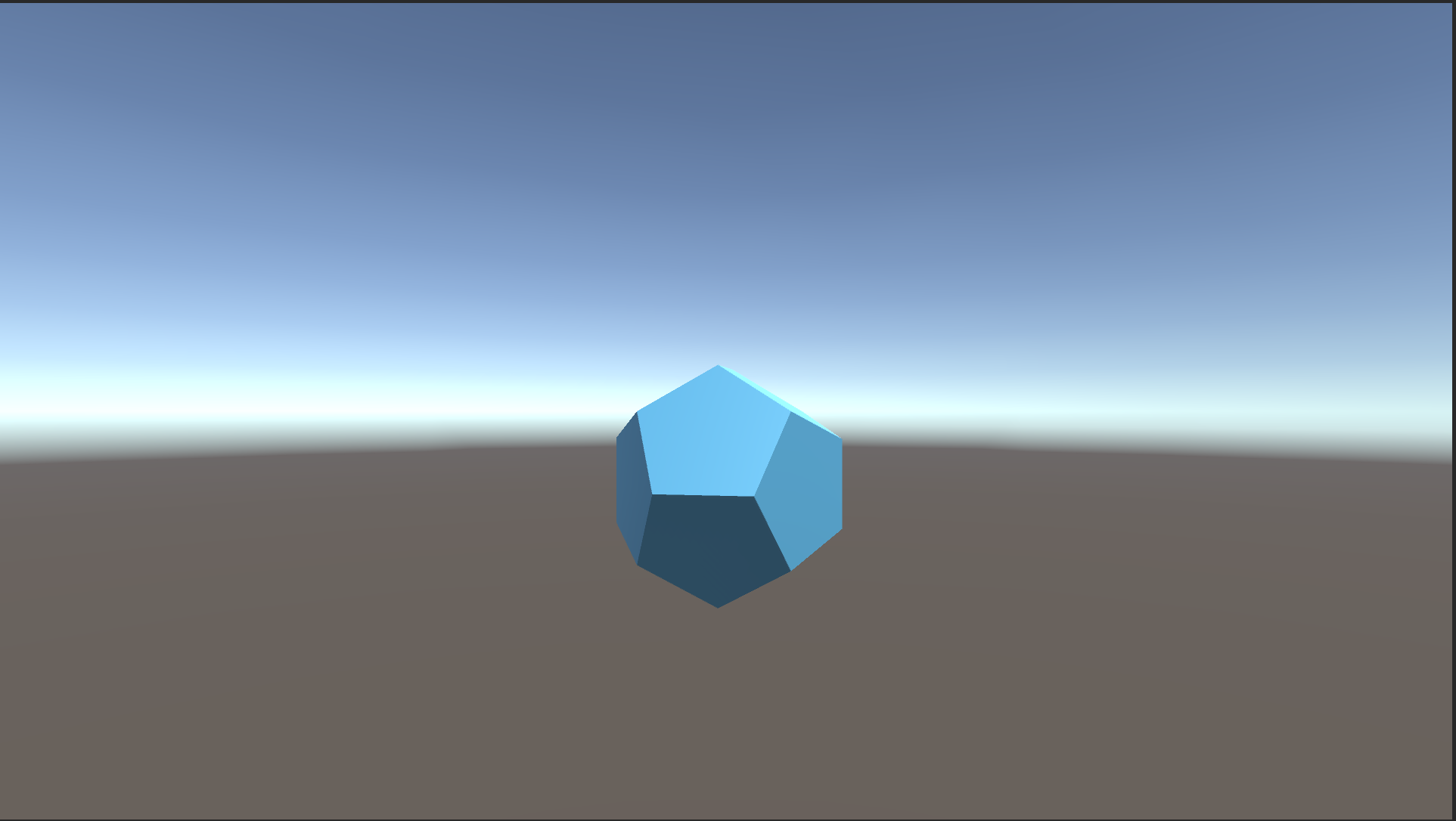
Unityで正十二面体を作りたくなって、作りました。
過去に投降した Unityで正多角柱（底面が正n角形の柱）をつくる方法～見た目が変にならないように～ と関連する内容になっています。
準備１（正十二面体について）
正十二面体の12個の各面は正五角形になっています。
正十二面体のWikipediaを見ると、頂点の座標情報が載っています。
12個の面の、反時計回りの頂点および中心の座標
頂点
${\displaystyle (0,\epsilon _{2}\phi ,\epsilon _{3}\phi ^{-1})}, {\displaystyle (-\epsilon _{2}\epsilon _{3},\epsilon _{2},\epsilon _{3})}, {\displaystyle (-\epsilon _{2}\epsilon _{3}\phi ^{-1},0,\epsilon _{3}\phi )}, {\displaystyle (\epsilon _{2}\epsilon _{3}\phi ^{-1},0,\epsilon _{3}\phi )}, {\displaystyle (\epsilon _{2}\epsilon _{3},\epsilon _{2},\epsilon _{3})}$
中心
$
{\displaystyle {\frac {\phi +2}{5}}(0,\epsilon _{2},\epsilon _{3}\phi )}
$
のxyz座標を偶置換した 12個
ここで $\phi$ は黄金比${\displaystyle {(1+{\sqrt {5}})/2}}$ 、 ${\displaystyle \epsilon _{2},\epsilon _{3}=\pm 1}$ です。
「xyz座標を偶置換」というのは、 $(x, y, z)$ を $(x, y, z)$ や $(z, x, y)$ や $(y, z, x)$ のように入れ替えるということです。
今回は、正十二面体の頂点がこのような座標になる理由などは全く考えずに、Unity上で正十二面体を作っていきます。
準備２（やること）
- Unityで新規プロジェクトを作成（3D Core）
- シーンを開きヒエラルキーから「3D Object > Quad」を作成（名前は「RegularDodecahedron」など）
- 新規スクリプト「RegularDodecahedron」を作成し、中身を以下のように書き換える。
using UnityEngine;
using UnityEditor;
public class RegularDodecahedron : MonoBehaviour
{
void Start()
{
Mesh mesh = RegularDodecahedronMesh();
SetMesh(mesh);
// SaveMesh(mesh, "Assets/Mesh/RegularDodecahedron.asset");
}
Mesh RegularDodecahedronMesh()// 正十二面体のメッシュを返す関数
{
float phi = (1 + Mathf.Sqrt(5))/2;// 黄金比
Mesh mesh = new Mesh();
Vector3[] vertices = new Vector3[60];// メッシュの頂点情報
int[] triangles = new int[108];// メッシュの三角形情報
int v = 0;// v : index for vertices
foreach(int epsilon2 in new int[2] {1, -1})
{
foreach(int epsilon3 in new int[2] {1, -1})
{
vertices[v++] = new Vector3(0, epsilon2*phi, epsilon3/phi);
vertices[v++] = new Vector3(-epsilon2*epsilon3, epsilon2, epsilon3);
vertices[v++] = new Vector3(-epsilon2*epsilon3/phi, 0, epsilon3*phi);
vertices[v++] = new Vector3(epsilon2*epsilon3/phi, 0, epsilon3*phi);
vertices[v++] = new Vector3(epsilon2*epsilon3, epsilon2, epsilon3);
}
}// ~20
for(v = 0; v < 20; v++)
{
vertices[v + 20] = new Vector3(vertices[v].z, vertices[v].x, vertices[v].y);
vertices[v + 40] = new Vector3(vertices[v].y, vertices[v].z, vertices[v].x);
}// ~60
int t = 0;// t : index for triangles
for(int s = 0; s < 12; s++)// s : index for surfaces
{
triangles[t++] = s*5 + 0;
triangles[t++] = s*5 + 1;
triangles[t++] = s*5 + 2;
triangles[t++] = s*5 + 0;
triangles[t++] = s*5 + 2;
triangles[t++] = s*5 + 3;
triangles[t++] = s*5 + 0;
triangles[t++] = s*5 + 3;
triangles[t++] = s*5 + 4;
}
mesh.name = "RegularDodecahedron";// meshの名前を設定
mesh.SetVertices(vertices);// meshに頂点情報を設定
mesh.SetTriangles(triangles, 0);// meshに三角形情報を設定
mesh.RecalculateNormals();// meshに法線ベクトルを設定
return mesh;
}
void SetMesh(Mesh mesh)// オブジェクトにメッシュを設定する関数
{
gameObject.GetComponent<MeshFilter>().sharedMesh = mesh;
gameObject.GetComponent<MeshCollider>().sharedMesh = mesh;
}
void SaveMesh(Mesh mesh, string path)// meshをpathに保存する関数
{
#if UNITY_EDITOR
AssetDatabase.CreateAsset(mesh, path);
AssetDatabase.SaveAssets();
#endif
}
}
- このスクリプトを先ほど作成したオブジェクトにくっつける。
- Playボタンを押す。
Quadが正十二面体に変わりました！
コードの解説（一部のみ）
int v = 0;// v : index for vertices
foreach(int epsilon2 in new int[2] {1, -1})
{
foreach(int epsilon3 in new int[2] {1, -1})
{
vertices[v++] = new Vector3(0, epsilon2*phi, epsilon3/phi);
vertices[v++] = new Vector3(-epsilon2*epsilon3, epsilon2, epsilon3);
vertices[v++] = new Vector3(-epsilon2*epsilon3/phi, 0, epsilon3*phi);
vertices[v++] = new Vector3(epsilon2*epsilon3/phi, 0, epsilon3*phi);
vertices[v++] = new Vector3(epsilon2*epsilon3, epsilon2, epsilon3);
}
}// ~20
この部分は、${\displaystyle \epsilon _{2},\epsilon _{3}=\pm 1}$について、「準備１」の座標をそのままメッシュの頂点に設定しています。「v++」の部分は v をインクリメント（プラス1）しています。
ここまでで、$2^2 \times 5 = 20$個の頂点が設定されました。
for(v = 0; v < 20; v++)
{
vertices[v + 20] = new Vector3(vertices[v].z, vertices[v].x, vertices[v].y);
vertices[v + 40] = new Vector3(vertices[v].y, vertices[v].z, vertices[v].x);
}// ~60
この部分は、先ほど設定した座標の偶置換を行っています。
ここまでで、すべてのメッシュの頂点が設定されました。
int t = 0;// t : index for triangles
for(int s = 0; s < 12; s++)// s : index for surfaces
{
triangles[t++] = s*5 + 0;
triangles[t++] = s*5 + 1;
triangles[t++] = s*5 + 2;
triangles[t++] = s*5 + 0;
triangles[t++] = s*5 + 2;
triangles[t++] = s*5 + 3;
triangles[t++] = s*5 + 0;
triangles[t++] = s*5 + 3;
triangles[t++] = s*5 + 4;
}
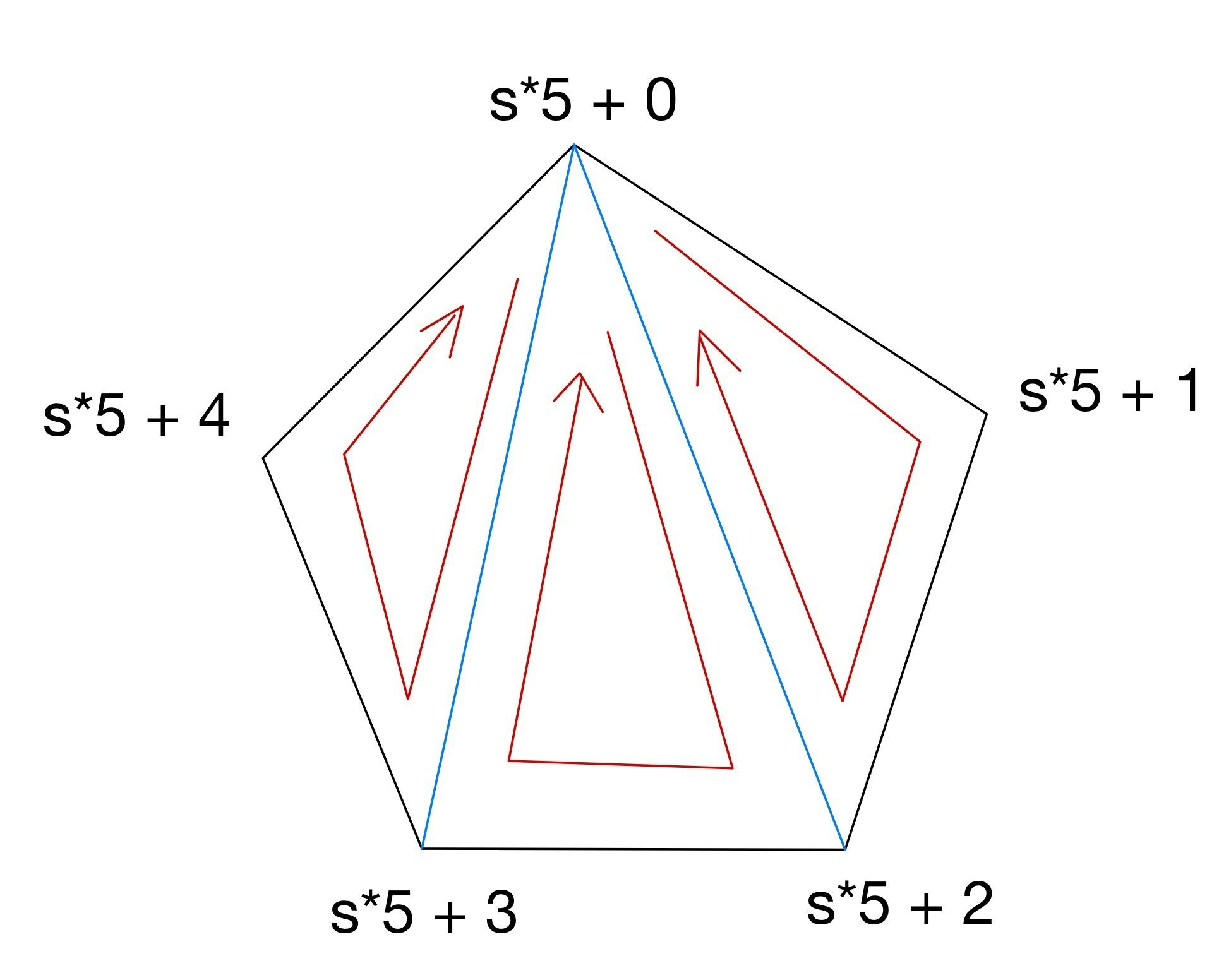
この部分は、12個の各面に対して、メッシュの三角形を設定しています。これは、メッシュの頂点が5つごとに一つの正五角形の頂点になっているという考えがもとになっています。
s番目の面におけるメッシュの三角形情報は以下のようなイメージになります。
メッシュの保存について
正十二面体を作ることはできたので、保存の方法を紹介したいと思います。このサイトを参考にさせていただきました。
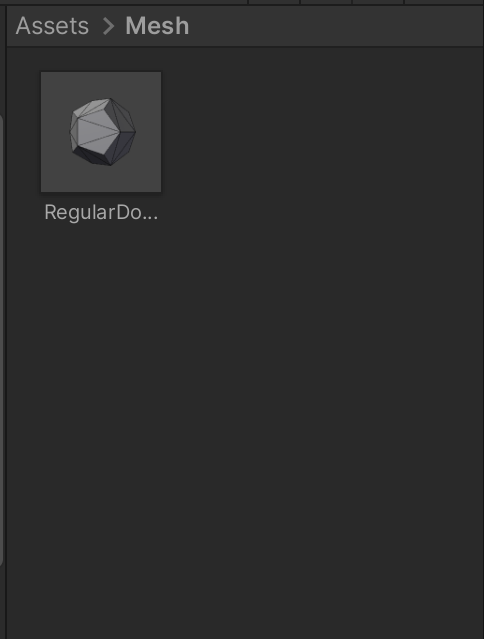
- まず、プロジェクトから「Assets」の直下に新規フォルダ「Mesh」を作成する。
- スクリプトの以下の部分のコメントアウトを外す。
SaveMesh(mesh, "Assets/Mesh/RegularDodecahedron.asset");
- Playボタンを押す。
メッシュを保存することができました。
保存したメッシュを適用する
次に、保存したメッシュを実際に適用してみたいと思います。
- シーンを開きヒエラルキーから「3D Object > Quad」を作成
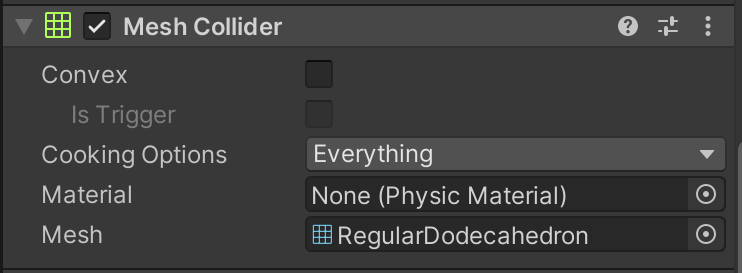
- インスペクターから、このオブジェクトのメッシュを変更する。
（「Mesh Filter」と「Mesh Collider」の2つのコンポーネントでメッシュを「Quad」から先ほど保存したものに変更する。）
↓
こうすると、Playボタンを押さなくても正十二面体の形が保たれるはずです。
補足
空のゲームオブジェクトではなく、Quadを作成するのは、わざわざコンポーネントを追加せずに済むようにするためです。
まとめ
Unityで正十二面体のメッシュを作って保存することができました。複雑な図形をUnity上で作ることができると達成感が味わえますよ。
それでは！