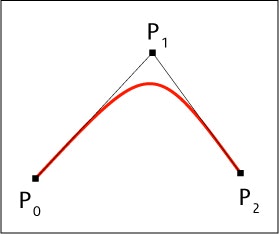
ベジエ2次曲線の長さを計算
ベジエ曲線の長さを計算する必要が出てきました。誤差はあってもいいのですが、やはり小さい方がいいです。そこで良い記事を見つけました。
■ Quadratic Bezier curve length
http://www.malczak.linuxpl.com/blog/quadratic-bezier-curve-length/
この記事を参考に Swift で書き直して見ました。
quadraticBezierLength.swift
func quadraticBezierLength(_ p0: CGPoint, _ p1: CGPoint, _ p2: CGPoint) -> CGFloat {
// cf. http://www.malczak.linuxpl.com/blog/quadratic-bezier-curve-length/
let a = CGPoint(p0.x - 2 * p1.x + p2.x, p0.y - 2 * p1.y + p2.y)
let b = CGPoint(2 * p1.x - 2 * p0.x, 2 * p1.y - 2 * p0.y)
let A = 4 * (a.x * a.x + a.y * a.y)
let B = 4 * (a.x * b.x + a.y * b.y)
let C = b.x * b.x + b.y * b.y
let Sabc = 2 * sqrt(A + B + C)
let A_2 = sqrt(A)
let A_32 = 2 * A * A_2
let C_2 = 2 * sqrt(C)
let BA = B / A_2
let L = (A_32 * Sabc + A_2 * B * (Sabc - C_2) + (4 * C * A - B * B) * log((2 * A_2 + BA + Sabc) / (BA + C_2))) / (4 * A_32)
return L
}
記事を疑うわけではありませんが、以前 Bezier曲線を計算する記事を元に。実際の曲線の点を細かくとってその点と点の距離の和を計算して、違いを計算して見ます。
approximateQuadraticBezierLength.swift
func approximateQuadraticBezierLength(_ p0: CGPoint, _ p1: CGPoint, _ p2: CGPoint) -> CGFloat {
let m = 1
let n = Int((p1 - p0).length + (p2 - p1).length) * m
var length: CGFloat = 0
var lastPt: CGPoint? = nil
for i in 0 ..< n {
let t = CGFloat(i) / CGFloat(n)
let q1 = p0 + (p1 - p0) * t
let q2 = p1 + (p2 - p1) * t
let r = q1 + (q2 - q1) * t
if let lastPt = lastPt {
length += (lastPt - r).length
}
lastPt = r
}
return length
}
実際に計算してみるとこんな感じです。
.swift
let p0 = CGPoint(0, 0)
let p1 = CGPoint(500, 0)
let p2 = CGPoint(500, 500)
approximateQuadraticBezierLength(p0, p1, p2) // 810.613036611711
quadraticBezierLength(p0, p1, p2) // 811.612620070115
どうでしょう。m の値を 10 と近似値の精度を上げる中間点を 10倍 に増やすと…
.swift
approximateQuadraticBezierLength(p0, p1, p2) // 811.512624236657
quadraticBezierLength(p0, p1, p2) // 811.612620070115
計算結果に収束しているような気もするので、良しとします。
コードは gist からも入手できます。
https://gist.github.com/codelynx/0f88983c0ba3e52776d2adeac77cb4f9
What's next?
ベジエの3次曲線の長さの計算ですね。ハードルはさらにたかそうです。
環境に関する表記
.log
Xcode Version 8.2.1 (8C1002)
Apple Swift version 3.0.2 (swiftlang-800.0.63 clang-800.0.42.1)