概要
RC直列回路の過渡現象を sympy で解析して(=回路方程式(微分方程式)を sympy で解析的に解いて)、その結果を matplotlib で描画します。具体的には、
$$ E = V_{R}(t) + V_{C}(t) $$
$$ E = R\cdot i(t) + \frac{1}{C}\int_{0}^{t}i(t),dt $$
という路方程式から、以下を求めて
$$ V_R(t) = E e^{- \frac{t}{C R}} $$ $$ V_C(t) = E \left(1 - e^{- \frac{t}{C R}}\right) $$
具体的なパラメータを与えてグラフに描画するところまでの内容です。
説明
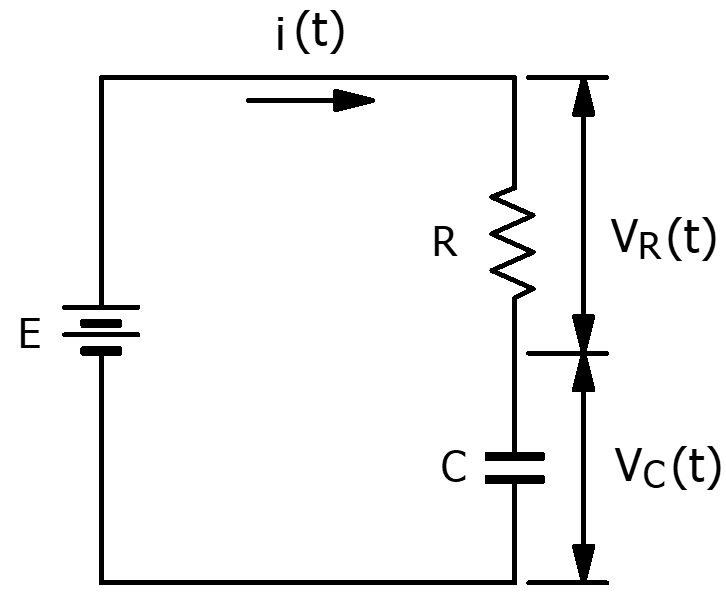
RC直列回路とは、次のように抵抗とコンデンサの直列接続した回路です。
この回路の回路方程式は、次のようになります。$R$ が抵抗値、$C$ がコンデンサの静電容量、$E$ が電源電圧、$i(t)$ が電流です。
$$ E = V_{R}(t) + V_{C}(t) $$
$$ E = R\cdot i(t) + \frac{1}{C}\int_{0}^{t}i(t),dt $$
sympy では積分項は扱いにくいので、次式のような電流 $i(t)$ と 電荷 $q(t)$ の関係を用いて微分の式に書き換えます。
$$ i(t) = \frac{d}{dt}q(t) $$
次のような微分方程式になりました。
$$ E = R\cdot \frac{d}{dt}q(t) + \frac{1}{C}\cdot q(t) $$
この方程式を $\rm{Eq.(1)}$ として sympy で定義します。シンボル $C1$ の意味については後ほど。
import sympy
import numpy as np
import matplotlib.pyplot as plt
# シンボル(変数記号)の定義
q,i = sympy.symbols('q i', cls=sympy.Function)
t,E,R,C,C1 = sympy.symbols('t E R C C1')
# 方程式 eq1 を立てる
eq1 = sympy.Eq( E, R * sympy.Derivative(q(t), t) + q(t)/C )
display(eq1)
sympy.latex(eq1)
実行結果
$$ E = R \frac{d}{d t} q{\left (t \right )} + \frac{1}{C} q{\left (t \right )} $$
この微分方程式を $q(t)$ について解きます。sympy で微分方程式を解くときは sympy.dsolve() を利用します。
$\rm{Eq.(1)}$ を、電荷 $q(t)$ について解いたものを $\rm{Eq.(2)}$ とします。
eq2 = sympy.dsolve(eq1, q(t))
display(eq2)
print(sympy.latex(eq2))
実行結果
$$ q{\left (t \right )} = C E + e^{\frac{1}{R} \left(C_{1} - \frac{t}{C}\right)} $$
ここで、$C_1$ は積分定数となります。時刻 $0$ でコンデンサに蓄えられている電荷はゼロであるという初期条件 $q(0)=0$ を利用して $C_1$ を求めます。
つまり、次の方程式 $\rm{Eq.(3)}$ を $C_1$ について解きます。
$$ 0 = CE + \exp({\frac{C_1}{R}}) $$
これは普通の方程式なので sympy.solve() で解きます。
# eq2の左辺を0、右辺にt=0を代入
eq3 = sympy.Eq(0, eq2.rhs.subs(t,0),)
C1a = sympy.solve(eq3,C1)[0]
display(C1a)
print(sympy.latex(C1a))
実行結果
$$ R \log{\left (- C E \right )} $$
求められた積分定数を $\rm{Eq.(2)}$ に代入して式を整理します。これを $\rm{Eq.(4)}$ とします。
# 初期条件を与えて求めた積分定数C1aを代入
eq4 = eq2.subs(C1,C1a)
display(eq4)
print(sympy.latex(eq4))
# 式を整理(展開)
eq4 = eq4.expand()
display(eq4)
print(sympy.latex(eq4))
実行結果
$$ q{\left (t \right )} = C E + e^{\frac{1}{R} \left(R \log{\left (- C E \right )} - \frac{t}{C}\right)} $$
$$ q{\left (t \right )} = C E - C E e^{- \frac{t}{C R}} $$
電荷 $q(t)$ を微分して 電流 $i(t)$ を求めます。この電流 $i(t)$ についての式を $\rm{Eq.(5)}$ とします。
# eq4 の右辺を t 微分
eq5 = sympy.Eq( i(t), sympy.diff(eq4.rhs,t))
display( eq5 )
print(sympy.latex(eq5))
実行結果
$$ i{\left (t \right )} = \frac{E}{R} e^{- \frac{t}{C R}} $$
電流 $i(t)$ を使って、抵抗の両端電圧 $V_R$ を求めます( $V_R=R\cdot i(t)$ )。また、コンデンサの両端電圧 $V_c$ を求めます( $V_C = E - V_R$ )
i = eq5.rhs
# 抵抗両端の電圧 VR
VR = R*i
display(VR)
# コンデンサ両端の電圧 VC
VC = E - VR
display(VC)
display(VC.collect(E)) # 電圧Eで括る
実行結果
$$ E e^{- \frac{t}{C R}} $$ $$ E - E e^{- \frac{t}{C R}}$$ $$ E \left(1 - e^{- \frac{t}{C R}}\right) $$
抵抗の両端電圧 $V_R$、コンデンサの両端電圧 $V_c$ が次のように求まりました。
$$ V_R(t) = E e^{- \frac{t}{C R}} $$ $$ V_C(t) = E \left(1 - e^{- \frac{t}{C R}}\right) $$
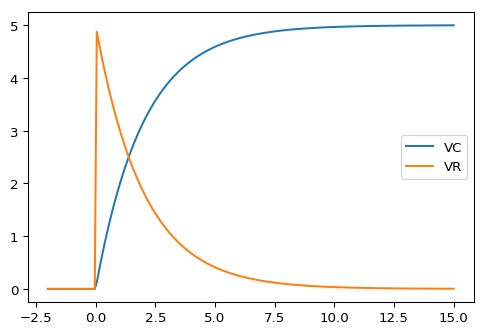
具体的な電源電圧 $E$、抵抗値 $R$、静電容量 $C$ を与えて、過渡現象をグラフを描画していきます。今回は、$E=5, (t\ge0)$、$R=50 \rm{k}\Omega$、$R=40 \mu\rm{F}$ として、時刻 $t=-2$ から $15$ までをプロットします。
lambdify を利用して、sympy オブジェクトを numpyユニバーサル関数に変換して利用します。
# パラメータ
prm = { E:sympy.Piecewise((0,t<0),(5,t>=0)), R:50e3, C:40e-6 }
# パラメータを代入
i = i.subs(prm)
VR=VR.subs(prm)
VC=VC.subs(prm)
# sympy オブジェクトを numpyユニバーサル関数に変換
f_VR = sympy.lambdify(t, VR, 'numpy')
f_VC = sympy.lambdify(t, VC, 'numpy')
tt = np.linspace(-2, 15, 200)
#
plt.figure()
plt.plot(tt, f_VC(tt),label='VC')
plt.plot(tt, f_VR(tt),label='VR')
plt.legend()
plt.show()
プログラム全体
%reset -f
import sympy
import numpy as np
import matplotlib.pyplot as plt
# シンボル(変数記号)の定義
q,i = sympy.symbols('q i', cls=sympy.Function)
t,E,R,C,C1 = sympy.symbols('t E R C C1')
# 方程式 eq1 を立てる
eq1 = sympy.Eq( E, R * sympy.Derivative(q(t), t) + q(t)/C )
display(eq1)
eq2 = sympy.dsolve(eq1, q(t))
display(eq2)
# eq2の左辺を0、右辺にt=0を代入
eq3 = sympy.Eq(0, eq2.rhs.subs(t,0),)
C1a = sympy.solve(eq3,C1)[0]
display(C1a)
# 初期条件を与えて求めた積分定数C1aを代入
eq4 = eq2.subs(C1,C1a)
display(eq4)
# 式を整理(展開)
eq4 = eq4.expand()
display(eq4)
# eq4 の右辺を t 微分
eq5 = sympy.Eq( i(t), sympy.diff(eq4.rhs,t))
display( eq5 )
i = eq5.rhs
# 抵抗両端の電圧 VR
VR = R*i
display(VR)
# コンデンサ両端の電圧 VC
VC = E - VR
display(VC)
display(VC.collect(E)) # 電圧Eで括る
# パラメータ
prm = { E:sympy.Piecewise((0,t<0),(5,t>=0)), R:50e3, C:40e-6 }
# パラメータを代入
i = i.subs(prm)
VR=VR.subs(prm)
VC=VC.subs(prm)
# sympy オブジェクトを numpyユニバーサル関数に変換
f_VR = sympy.lambdify(t, VR, 'numpy')
f_VC = sympy.lambdify(t, VC, 'numpy')
tt = np.linspace(-2, 15, 200)
#
plt.figure(dpi=96)
plt.plot(tt, f_VC(tt),label='VC')
plt.plot(tt, f_VR(tt),label='VR')
plt.legend()
plt.show()