概要
書籍「つくりながら学ぶ!深層強化学習」の「第2章 迷路課題に強化学習を実装しよう」の学習の記録&メモです。本のなかでは Python + numpy でロジックを構成し、迷路内の移動の様子などを Matplotlib により可視化していますが、これを F# + Math.NET Numerics でロジック構成して WPF で可視化しています。
- 正誤表を必ず確認しましょう。初版では p.46 に記載されている方策勾配法に関する重要な式に誤りがあります。
紙面(初版)では、次のようになっていますが、、、
\begin{align}
\theta_{s_i,a_j}&= \theta_{s_i,a_j}+\eta\cdot \Delta \theta_{s_i,a_j}\\
\Delta\theta_{s_i,a_j} &=\frac{N(s_i,a_j)+P(s_i,a_j)\cdot N(s_i,a)}{T}
\end{align}
正誤表によれば次式が正しいものになります(符号が変わっています)。
\begin{align}
\theta_{s_i,a_j}&= \theta_{s_i,a_j}+\eta\cdot \Delta \theta_{s_i,a_j}\\
\Delta\theta_{s_i,a_j} &=\frac{N(s_i,a_j)-P(s_i,a_j)\cdot N(s_i,a)}{T}
\end{align}
準備
ゴールを目指して迷路内を移動するエージェント(=強化学習における行動の主体)の実装のために行列計算が必要となります。Pythonにおける行列計算では numpy が定番ですが、.NET環境になるので、Math.NET Numerics という科学技術計算ライブラリを使用することにしました(はじめての利用です)。NuGetパッケージマネージャから「MathNet」をキーワードに検索して、MathNet.NumericsとMathNet.Numerics.FSharpをインストールします。
迷路課題
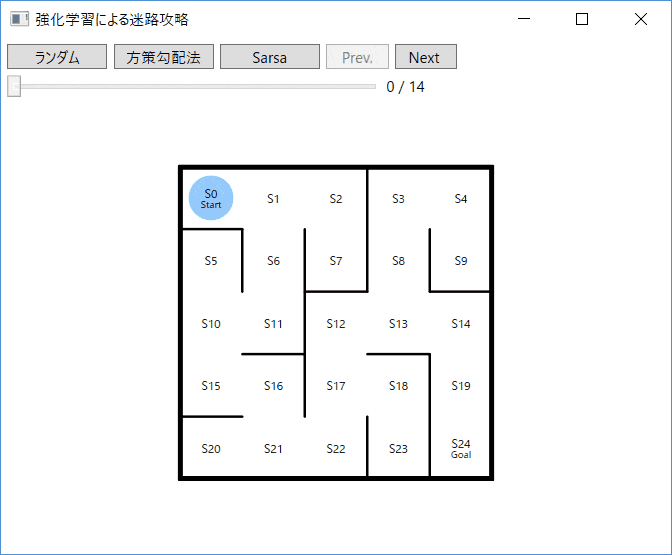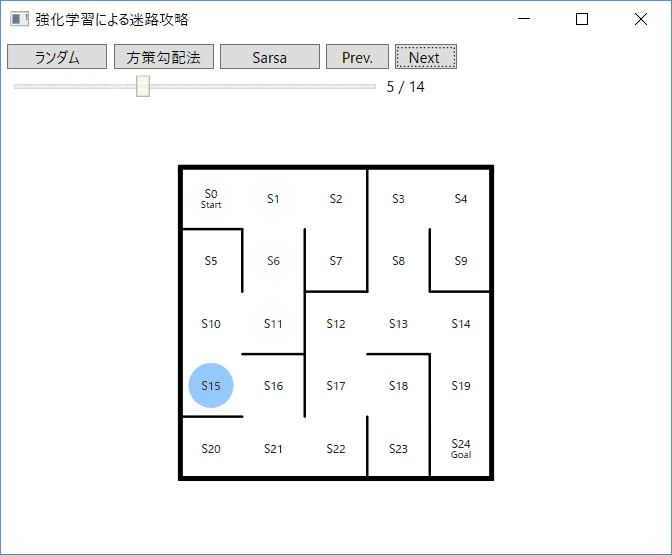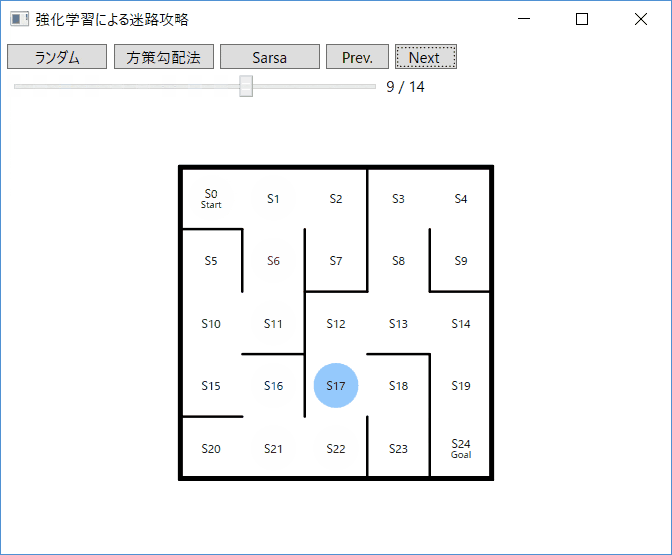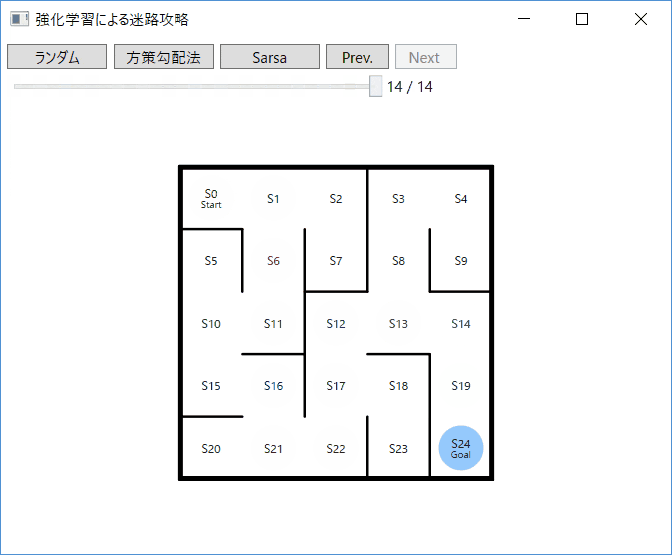
本のなかで取り上げられているものは 3×3マス の迷路ですが、ここでは 5×5マス に拡張した次のような迷路を攻略対象とします。この迷路について、S0 をスタートして、最短経路で S24 のゴールを目指すようなエージェントを実装することを目的とします(Sは状態「State」の頭文字)。最短経路は S0 → S1 → S6 → S11 → S10 → S15 → S16 → S21 → S22 → S17 → S12 → S13 → S14 → S19 → S24(14ステップの移動)となります。
迷路内の S0 から S23 の各状態(各位置)においてエージェントが選択可能な行動(上・右・下・左の方向への移動)を、行列 $\theta_0$(theta_0)として定義します。なお、S24はゴール地点なので、そこで選択できる行動はありませんので定義しません。この$\theta_0$とスタートならびにゴール地点を、迷路を解くための最低限の情報として強化学習のロジックに与えます。例えば、theta_0の1行目が [nan;1.;nan;nan] となっていますが、これは 状態S0 において各方向(上・右・下・左の順)に移動可能かどうかを表現(=1.が移動可能、nanが移動不可能を意味)しており、具体的には、その状態(=S0)でエージェントが「右」に移動する行動を選択することができる、という情報を与えています。
let theta_0 = matrix [[nan; 1. ; nan; nan] // S0
[nan; 1. ; 1. ; 1. ] // S1
[nan; nan; 1. ; 1. ] // S2
[nan; 1. ; 1. ; nan] // S3
[nan; nan; 1. ; 1. ] // S4
(/* 略 */)
[nan; 1. ; nan; nan] // S20
[1. ; 1. ; nan; 1. ]
[1. ; nan; nan; 1. ]
[1. ; nan; nan; nan]]
F#では、整数と浮動小数点数の自動変換(キャスト)はしてくれません(1 + 1.2はコンパイルエラーになります、1.0 + 1.2と書かないとダメ)。そのため、float型の数値リテラルは明示的に1.もしくは1.0のように記述する必要があります(単に1と記述するとint型として解釈されてしまいます)。また、nanは非数値(Not a Number)を表します(numpy における numpy.nan に相当します)。
ランダム移動による探索
迷路内をただひたすらにランダムに移動してゴールを目指す手法です。
先ほどのtheta_0に基づいて、ランダムに移動するための方策 $\pi_0$(pi_0)を作成します。ある状態(位置)において、移動可能な方向が2つであればそれぞれを50%の割合で選択、3つであればそれぞれ33.3%の確率で選択するような選択確率を表現した行列(pi_0)を作成します。
つまり、さきほどのtheta_0を入力として、次のような行列 pi_0 を出力するような関数(simpleConvertIntoPiFromTheta)を定義します。例えば、2行目の[nan; 1. ; 1. ; 1. ]は、状態S1では33.3%の確率で右移動、33.3%の確率で下移動、33.3%の確率で左移動するという方策をとることを意味しています。
DenseMatrix 24x4-Double
0 1 0 0
0 0.333333 0.333333 0.333333
0 0 0.5 0.5
0 0.5 0.5 0
0 0 0.5 0.5
0 0 1 0
0.5 0 0.5 0
1 0 0 0
.. .. .. ..
0 1 0 0
0.333333 0.333333 0 0.333333
0.5 0 0 0.5
1 0 0 0
theta_0からpi_0を求める関数simpleConvertIntoPiFromThetaは次のように実装しました。引数に$\theta_0$を与えて、戻値として$\pi_0$を得ます。なお、numpyには、nanは無視して合計を求める関数np.nansumが用意されていますが、Math.NET Numericsでそれに相当するものが見つけられなかったので自作しています。
let nanToZero f = if Double.IsNaN(f) then 0. else f
let nanSum (v:Vector<float>) =
v |> Vector.fold (fun s i -> s + (nanToZero i) ) 0.
let simpleConvertIntoPiFromTheta theta =
theta |> Matrix.mapRows (fun _ v -> v / (nanSum v) )
|> Matrix.map nanToZero
Matrix.mapRowsは行単位で所謂map(射影操作)を適用します。入力の行列サイズと出力サイズは同じになります。操作として与える関数の第一引数には「何行目かの情報」がint型で、第二引数には「行」がvector型で与えられます。
次に、迷路内の各状態(位置)において方策pi_0に基づく確率で行動(移動方向)を決め、ゴールを目指す関数goalMazeを定義します。引数には、初期位置0(=S0)、目的位置24(=S24)、迷路情報(tehta_0)を与えます。戻値は、迷路内の移動履歴(S0 → ・・・ → S24)をリスト形式で表現したものとなります。関数型らしく再帰を使って実装しました。
let goalMaze theta start goal =
let pi = theta |> simpleConvertIntoPiFromTheta
let rec goalMaze' pi cS goal =
let nS = getNextState pi cS
if nS = goal then goal::[] else nS::(goalMaze' pi nS goal)
start::(goalMaze' pi start goal)
プログラム全体は次のようになります(GUI版ではありません)。
open System
open MathNet.Numerics.LinearAlgebra
open MathNet.Numerics.Random
type Direction =
| Up = 0
| Right = 1
| Down = 2
| Left = 3
| NA = 4
let nanToZero f = if Double.IsNaN(f) then 0. else f
let mazeWidth = 5
let isNan f = Double.IsNaN(f)
let isNotNan f = Double.IsNaN(f) |> not
let nanSum (v:Vector<float>) =
v |> Vector.fold (fun s i -> s + (nanToZero i) ) 0.
let rand = new MersenneTwister ()
let randomChoice pArray =
let th = rand.NextDouble ()
pArray |> Vector.toSeq
|> Seq.scan (fun sum p -> sum + p ) 0.
|> Seq.skip 1
|> Seq.findIndex (fun p -> p >= th )
let simpleConvertIntoPiFromTheta theta =
theta |> Matrix.mapRows (fun _ v -> v / (nanSum v) )
|> Matrix.map nanToZero
let getNextState (pi:Matrix<float>) currentState =
let action = currentState
|> pi.Row
|> randomChoice
|> enum<Direction>
match action with
| Direction.Up -> currentState - mazeWidth
| Direction.Right -> currentState + 1
| Direction.Down -> currentState + mazeWidth
| Direction.Left -> currentState - 1
| _ -> raise <| System.IndexOutOfRangeException ()
let goalMaze theta start goal =
let pi = theta |> simpleConvertIntoPiFromTheta
let rec goalMaze' pi cS goal =
let nS = getNextState pi cS
if nS = goal then goal::[] else nS::(goalMaze' pi nS goal)
start::(goalMaze' pi start goal)
[<EntryPoint>]
let main argv =
let theta_0 = matrix [[nan; 1. ; nan; nan] // S0
[nan; 1. ; 1. ; 1. ]
[nan; nan; 1. ; 1. ]
[nan; 1. ; 1. ; nan]
[nan; nan; 1. ; 1. ]
[nan; nan; 1. ; nan] // S5
[1. ; nan; 1. ; nan]
[1. ; nan; nan; nan]
[1. ; nan; 1. ; nan]
[1. ; nan; nan; nan]
[1. ; 1. ; 1. ; nan] // S10
[1. ; nan; nan; 1. ]
[nan; 1. ; 1. ; nan]
[1. ; 1. ; nan; 1. ]
[nan; nan; 1. ; 1. ]
[1. ; 1. ; nan; nan] // S15
[nan; nan; 1. ; 1. ]
[1. ; 1. ; 1. ; nan]
[nan; nan; 1. ; 1. ]
[1. ; nan; 1. ; nan]
[nan; 1. ; nan; nan] // S20
[1. ; 1. ; nan; 1. ]
[1. ; nan; nan; 1. ]
[1. ; nan; nan; nan]]
let result = goalMaze theta_0 0 24
do Console.WriteLine ( sprintf "ステップ数は%dでした。" <| result.Length - 1)
do Console.WriteLine ( sprintf "%A" result )
do Console.ReadKey() |> ignore
0
実行結果の一例は、次のようになります(当然ながら結果は毎回変化します)。
ステップ数は312でした。
[0; 1; 0; 1; 0; 1; 6; 1; 2; 7; 2; 7; 2; 1; 2; 1; 6; 11; 10; 5; 10; 5; 10; 5; 10;
11; 6; 11; 6; 1; 6; 11; 6; 11; 6; 11; 6; 1; 6; 11; 6; 1; 2; 7; 2; 1; 0; 1; 0; 1;
2; 7; 2; 7; 2; 7; 2; 1; 2; 1; 6; 1; 6; 1; 0; 1; 0; 1; 0; 1; 2; 7; 2; 1; 2; 1; 2;
7; 2; 1; 6; 1; 2; 7; 2; 7; 2; 1; 0; 1; 0; 1; 2; 7; 2; 1; 0; 1; 0; 1; ...]
20,000回試行した結果、平均ステップ数(平均移動回数)は326、最小ステップ数は18、最大ステップ数は2408でした。残念ながら最適解である14ステップの経路をつくることはできませんでした。
メモ
行止りでない限りは、「直前の状態に戻る」という意味のない行動を制限するだけでも、ずいぶん改善できるような気がします。でも、そういった問題構造や問題特性に関する情報、さらには「迷路を解いている」という情報すら得られない条件のもとで、自身の学習のみで賢くなっていくのが強化学習のポイントでもあるので、変なことはしないほうが良い?
方策勾配法による学習
方策反復法のひとつである方策勾配法による迷路攻略を実装します。理論については「その2」でまとめたいと思います。今回はプログラムのみを示します。
実装
open System
open MathNet.Numerics.LinearAlgebra
open MathNet.Numerics.Random
type Direction =
| Up = 0
| Right = 1
| Down = 2
| Left = 3
| NA = 4
let nanToZero f = if Double.IsNaN(f) then 0. else f
let mazeWidth = 5
let isNan f = Double.IsNaN(f)
let isNotNan f = Double.IsNaN(f) |> not
let nanSum (v:Vector<float>) =
v |> Vector.fold (fun s i -> s + (nanToZero i) ) 0.
let rand = new MersenneTwister ()
let randomChoice pArray =
let th = rand.NextDouble ()
pArray |> Vector.toSeq
|> Seq.scan (fun sum p -> sum + p ) 0.
|> Seq.skip 1
|> Seq.findIndex (fun p -> p >= th )
let simpleConvertIntoPiFromTheta theta =
theta |> Matrix.mapRows (fun _ v -> v / (nanSum v) )
|> Matrix.map nanToZero
let softmaxConvertIntoPiFromTheta theta =
let beta = 1.
theta |> Matrix.mapRows (fun _ v -> ( beta*v |>Vector.Exp ) / ( beta*v |> Vector.Exp |> nanSum ) )
|> Matrix.map nanToZero
let getActionAndNextState (pi:Matrix<float>) currentState =
let action = currentState
|> pi.Row
|> randomChoice
|> enum<Direction>
let nextState = match action with
| Direction.Up -> currentState - mazeWidth
| Direction.Right -> currentState + 1
| Direction.Down -> currentState + mazeWidth
| Direction.Left -> currentState - 1
| _ -> raise <| System.IndexOutOfRangeException ("???")
(action, nextState)
let updateTheta (theta:Matrix<float>) (pi:Matrix<float>) (saHistory:List<int*Direction>) =
let eta = 0.2
let t = saHistory |> List.length |> float
let sCount = Seq.init theta.RowCount (fun _ -> 0.) |> vector
let saCount =Seq.init theta.RowCount (fun _ -> Seq.init theta.ColumnCount (fun _ -> 0. )) |> matrix
for sa in saHistory do
if snd sa <> Direction.NA then
let s = fst sa
let a = snd sa |> int
do sCount.Item(s) <- sCount.At(s) + 1.
do saCount.Item(s,a) <- saCount.At(s,a) + 1.
let dTheta = theta |> Matrix.map (fun _ -> 0. )
for s in 0..(pi.RowCount-1) do
for a in 0..(pi.ColumnCount-1) do
if theta.At(s,a) |> isNotNan then
do dTheta.Item(s,a) <- (( saCount.At(s,a) - pi.At(s,a) * sCount.At(s) ) / t)
theta + ( eta * dTheta )
let rec goalMaze'' pi cS goal =
let a,nS = getActionAndNextState pi cS
if nS = goal then
(cS,a)::(nS,Direction.NA)::[]
else
(cS,a)::(goalMaze'' pi nS goal)
let rec goalMaze' theta pi start goal loopNum =
let stopEpsilon = 0.002
let saHistory = (start,Direction.NA)::(goalMaze'' pi start goal) |> List.tail
let newTheta = updateTheta theta pi saHistory
let newPi = newTheta |> softmaxConvertIntoPiFromTheta
let epsilon = ( pi - newPi ) |> Matrix.Abs |> Matrix.sum
if epsilon > stopEpsilon then
goalMaze' newTheta newPi start goal (loopNum+1)
else
saHistory, loopNum+1
let goalMaze theta start goal =
let pi_0 = theta |> softmaxConvertIntoPiFromTheta
let saHistory, loopNum = goalMaze' theta pi_0 start goal 0
Console.WriteLine (sprintf "loopNum = %d" loopNum )
saHistory |> List.map (fun a -> fst a )
[<EntryPoint>]
let main argv =
let theta_0 = matrix [[nan; 1. ; nan; nan] // S01
[nan; 1. ; 1. ; 1. ]
[nan; nan; 1. ; 1. ]
[nan; 1. ; 1. ; nan]
[nan; nan; 1. ; 1. ]
[nan; nan; 1. ; nan] // S05
[1. ; nan; 1. ; nan]
[1. ; nan; nan; nan]
[1. ; nan; 1. ; nan]
[1. ; nan; nan; nan]
[1. ; 1. ; 1. ; nan] // S10
[1. ; nan; nan; 1. ]
[nan; 1. ; 1. ; nan]
[1. ; 1. ; nan; 1. ]
[nan; nan; 1. ; 1. ]
[1. ; 1. ; nan; nan] // S15
[nan; nan; 1. ; 1. ]
[1. ; 1. ; 1. ; nan]
[nan; nan; 1. ; 1. ]
[1. ; nan; 1. ; nan]
[nan; 1. ; nan; nan] // S20
[1. ; 1. ; nan; 1. ]
[1. ; nan; nan; 1. ]
[1. ; nan; nan; nan]]
let result = goalMaze theta_0 0 24
do Console.WriteLine ( sprintf "ステップ数は%dでした。" <| result.Length - 1)
do Console.WriteLine ( sprintf "%A" result )
do Console.ReadKey() |> ignore
0
実行結果の一例は、次のようになります(結果は毎回変化します)。
loopNum = 7407
ステップ数は14でした。
[0; 1; 6; 11; 10; 15; 16; 21; 22; 17; 12; 13; 14; 19; 24]
内部的には7,500回前後のループ処理(強化学習)を行なっており、その結果として最終的に最短経路での移動ができるようになっています。実行時間は i7-7600U のノートパソコンで 1分15秒 程度でした。実は、当初、方策の更新式を誤って実装していたのですが、そのときは15秒程度で14ステップの最短経路を見つけることができていました。それが、更新式を修正したら時間的には大幅に悪化してしまいました。学習率 $\eta$(eta)と、学習終了に関するパラメータ $\epsilon$(epsilon)に関しての調整が必要になりそうです。
感想
ここには載せていませんがGUI(WPF+F#)の実装に予測をはるかに超える時間をとられてしまい、目標としていたスピードで進められませんでした(探索ロジックの実装にかかった時間を1とすると、結果の可視化・GUIの実装には5ぐらいかかってしまいました)。期限までに1エントリを作成するという約束をしていたので、とりあえずアップした状況です。
次は、方策勾配法の解説と、SarsaとQ学習の実装を目標にします。
参考資料
- 小川雄太郎 著「つくりながら学ぶ!深層強化学習」マイナビ出版
- 上記書籍のサポートリポジトリ@GitHub
- 大槻知史 著「最強囲碁AI アルファ碁 解体新書(増補改訂版)」翔泳社